Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Rahman, Q.I
1988.
The univalence of a linear combination of convex mappings.
Journal of Mathematical Analysis and Applications,
Vol. 135,
Issue. 2,
p.
419.
Bhargava, S.
and
Rao, S. Nanjunda
1989.
On linear combinations of n convex functions of order a.
International Journal of Mathematical Education in Science and Technology,
Vol. 20,
Issue. 1,
p.
151.
Bhowmik, Bappaditya
and
Biswas, Souvik
2025.
Distortion, Radius of Concavity and Several Other Radii Results for Certain Classes of Functions.
Computational Methods and Function Theory,
Vol. 25,
Issue. 2,
p.
393.

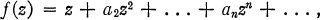

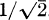 .
.