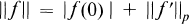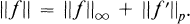Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Kolaski, Clinton J.
1988.
Isometries of some smooth normed spaces of analytic functions.
Complex Variables, Theory and Application: An International Journal,
Vol. 10,
Issue. 2-3,
p.
115.
1993.
Composition Operators on Function Spaces.
Vol. 179,
Issue. ,
p.
273.
Hornor, William
and
Jamison, James E.
2001.
Isometries of some Banach spaces of analytic functions.
Integral Equations and Operator Theory,
Vol. 41,
Issue. 4,
p.
410.
Geng, Li-Gang
Zhou, Ze-Hua
and
Dong, Xing-Tang
2012.
Isometric composition operators on weighted Dirichlet-type spaces.
Journal of Inequalities and Applications,
Vol. 2012,
Issue. 1,
JAMISON, JAMES
and
KING, RAENA
2014.
UNBOUNDED HERMITIAN OPERATORS ON KOLASKI SPACES.
Glasgow Mathematical Journal,
Vol. 56,
Issue. 3,
p.
507.
Koshimizu, Hironao
2014.
Linear isometries on spaces consisting of absolutely continuous functions.
Acta Scientiarum Mathematicarum,
Vol. 80,
Issue. 3-4,
p.
581.
Moradi, Abbas
Hedayatian, Karim
Robati, Bahram Khani
and
Ansari, Mohammad
2015.
Non supercyclic subsets of linear isometries on Banach spaces of analytic functions.
Czechoslovak Mathematical Journal,
Vol. 65,
Issue. 2,
p.
389.
Lin, Qingze
Liu, Junming
and
Wu, Yutian
2018.
Volterra type operators on Sp(D) spaces.
Journal of Mathematical Analysis and Applications,
Vol. 461,
Issue. 2,
p.
1100.
Gu, Caixing
and
Luo, Shuaibing
2018.
Composition and multiplication operators on the derivative Hardy space.
Complex Variables and Elliptic Equations,
Vol. 63,
Issue. 5,
p.
599.
Ueki, Sei-Ichiro
2020.
Isometries of Analytic Function Spaces with $$N^{p}$$-Derivative.
Integral Equations and Operator Theory,
Vol. 92,
Issue. 3,
Gupta, Anuradha
and
Gupta, Bhawna
2020.
On k-composition and k-Hankel composition operators on the derivative Hardy space.
Banach Journal of Mathematical Analysis,
Vol. 14,
Issue. 4,
p.
1602.
Geng, Ligang
2021.
Isometric multiplication operators and weighted composition operators of BMOA.
Journal of Inequalities and Applications,
Vol. 2021,
Issue. 1,
Ueki, Sei-Ichiro
2023.
Isometries of Analytic Besov-Type Bergman-Orlicz Spaces on the Unit Disk.
Mediterranean Journal of Mathematics,
Vol. 20,
Issue. 1,
Miura, Takeshi
and
Niwa, Norio
2023.
Surjective isometries on a Banach space of analytic functions with bounded derivatives.
Acta Scientiarum Mathematicarum,
Vol. 89,
Issue. 1-2,
p.
109.
Jiménez-Vargas, A.
and
Miura, Takeshi
2023.
Approximate local isometries of derivative Hardy spaces.
Quaestiones Mathematicae,
Vol. 46,
Issue. 1,
p.
23.
Lin, Qingze
and
Xie, Huayou
2025.
Cesàro-type operators on derivative-type Hilbert spaces of analytic functions: The proof of a conjecture.
Journal of Functional Analysis,
Vol. 288,
Issue. 6,
p.
110813.