Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Lasser, Rupert
1983.
Bochner theorems for hypergroups and their applications to orthogonal polynomial expansions.
Journal of Approximation Theory,
Vol. 37,
Issue. 4,
p.
311.
Verma, A.
and
Jain, V. K.
1985.
Number Theory.
Vol. 1122,
Issue. ,
p.
206.
Gasper, George
1985.
Rogers’ Linearization Formula for the Continuous q-Ultraspherical Polynomials and Quadratic Transformation Formulas.
SIAM Journal on Mathematical Analysis,
Vol. 16,
Issue. 5,
p.
1061.
Rahman, Mizan
and
Verma, Arun
1986.
A q-integral representation of Rogers' q-ultraspherical polynomials and some applications.
Constructive Approximation,
Vol. 2,
Issue. 1,
p.
1.
Gasper, George
and
Rahman, Mizan
1986.
Positivity of the Poisson Kernel for the Continuous q-Jacobi Polynomials and Some Quadratic Transformation Formulas for Basic Hypergeometric Series.
SIAM Journal on Mathematical Analysis,
Vol. 17,
Issue. 4,
p.
970.
Rahman, Mizan
1986.
A product formula for the continuous q-Jacobi polynomials.
Journal of Mathematical Analysis and Applications,
Vol. 118,
Issue. 2,
p.
309.
Suslov, S. K.
1987.
Classical orthogonal polynomials of a discrete variable continuous orthogonality relation.
Letters in Mathematical Physics,
Vol. 14,
Issue. 1,
p.
77.
Gasper, George
1989.
q-Extensions of Clausen’s Formula and of the Inequalities Used by de Branges in His Proof of the Bieberbach, Robertson, and Milin Conjectures.
SIAM Journal on Mathematical Analysis,
Vol. 20,
Issue. 4,
p.
1019.
Connett, W. C.
Markett, C.
and
Schwartz, A. L.
1991.
Probability Measures on Groups X.
p.
45.
Rahman, Mizan
and
Verma, Arun
1993.
Quadratic transformation formulas for basic hypergeometric series.
Transactions of the American Mathematical Society,
Vol. 335,
Issue. 1,
p.
277.
Rahman, Mizan
and
Suslov, Sergei K.
1994.
The Pearson Equation and the Beta Integrals.
SIAM Journal on Mathematical Analysis,
Vol. 25,
Issue. 2,
p.
646.
Markett, Clemens
1994.
Linearization of the product of symmetric orthogonal polynomials.
Constructive Approximation,
Vol. 10,
Issue. 3,
p.
317.
1995.
Harmonic Analysis of Probability Measures on Hypergroups.
p.
553.
Álvarez-Nodarse, R.
Arvesú, J.
and
Yáñez, R.J.
2001.
On the Connection and Linearization Problem for Discrete Hypergeometric q-Polynomials.
Journal of Mathematical Analysis and Applications,
Vol. 257,
Issue. 1,
p.
52.
Novaes, M
Hornos, J E M
and
Bernardes, E S
2003.
Harmonic functions ofsuq(2) forq andq S1.
Journal of Physics A: Mathematical and General,
Vol. 36,
Issue. 24,
p.
6733.
Kokologiannaki, C. G.
Siafarikas, P. D.
and
Stabolas, J. D.
2003.
Nonlinear Analysis and Applications: To V. Lakshmikantham on his 80th Birthday.
p.
671.
Szwarc, Ryszard
2005.
Theory and Applications of Special Functions.
Vol. 13,
Issue. ,
p.
461.
Haine, Luc
and
Iliev, Plamen
2006.
Askey-Wilson type functions with bound states.
The Ramanujan Journal,
Vol. 11,
Issue. 3,
p.
285.
Suslov, Sergei K.
and
Trey, Benjamin
2008.
The Hahn polynomials in the nonrelativistic and relativistic Coulomb problems.
Journal of Mathematical Physics,
Vol. 49,
Issue. 1,
Chaggara, Hamza
and
Koepf, Wolfram
2010.
On linearization coefficients of Jacobi polynomials.
Applied Mathematics Letters,
Vol. 23,
Issue. 5,
p.
609.
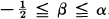 . However, an exact formula in a hypergeometric series form for general α, β has been very elusive so far, in spite of the fact that all computation of special cases seemed to indicate that such a formula should exist.
. However, an exact formula in a hypergeometric series form for general α, β has been very elusive so far, in spite of the fact that all computation of special cases seemed to indicate that such a formula should exist.
