Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T06:11:23.481Z Has data issue: false hasContentIssue false
  • English
  • Français

Lipschitz-free Spaces on Finite Metric Spaces

Part of: General convexity Nontrigonometric harmonic analysis Analysis on metric spaces Normed linear spaces and Banach spaces; Banach lattices

Published online by Cambridge University Press:  13 February 2019

Stephen J. Dilworth ,
Denka Kutzarova  and
Mikhail I. Ostrovskii
Stephen J. Dilworth
Affiliation:
Department of Mathematics, University of South Carolina, Columbia, SC 29208, USA Email: dilworth@math.sc.edu
Denka Kutzarova
Affiliation:
Department of Mathematics University of Illinois at Urbana-Champaign Urbana, IL 61801, USA Institute of Mathematics and Informatics, Bulgarian Academy of Sciences Email: denka@math.uiuc.edu
Mikhail I. Ostrovskii
Affiliation:
Department of Mathematics and Computer Science, St. John’s University, 8000 Utopia Parkway, Queens, NY 11439, USA Email: ostrovsm@stjohns.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Main results of the paper are as follows:

(1) For any finite metric space 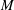$M$ the Lipschitz-free space on 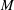$M$ contains a large well-complemented subspace that is close to 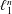$\ell _{1}^{n}$.

(2) Lipschitz-free spaces on large classes of recursively defined sequences of graphs are not uniformly isomorphic to 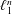$\ell _{1}^{n}$ of the corresponding dimensions. These classes contain well-known families of diamond graphs and Laakso graphs.

Interesting features of our approach are: (a) We consider averages over groups of cycle-preserving bijections of edge sets of graphs that are not necessarily graph automorphisms. (b) In the case of such recursive families of graphs as Laakso graphs, we use the well-known approach of Grünbaum (1960) and Rudin (1962) for estimating projection constants in the case where invariant projections are not unique.

Keywords

Arens–Eells spacediamond graphearth mover distanceKantorovich–Rubinstein distanceLaakso graphLipschitz-free spacerecursive family of graphstransportation costWasserstein distance

MSC classification

Primary: 52A21: Finite-dimensional Banach spaces (including special norms, zonoids, etc.)
Secondary: 30L05: Geometric embeddings of metric spaces 42C10: Fourier series in special orthogonal functions (Legendre polynomials, Walsh functions, etc.) 46B07: Local theory of Banach spaces 46B20: Geometry and structure of normed linear spaces 46B85: Embeddings of discrete metric spaces into Banach spaces; applications in topology and computer science
Type
Article
Information
Canadian Journal of Mathematics , Volume 72 , Issue 3 , June 2020 , pp. 774 - 804
Copyright
© Canadian Mathematical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

Author S. D. was supported by the National Science Foundation under Grant Number DMS–1361461. Authors S. D. and D. K. were supported by the Workshop in Analysis and Probability at Texas A&M University in 2017. Author M. O. was supported by the National Science Foundation under Grant Number DMS–1700176.

References

Andoni, A., Do Ba, K., Indyk, P., and Woodruff, D., Efficient sketches for earth-mover distance, with applications. In: 2009 50th Annual IEEE Symposium on Foundations of Computer Science FOCS 2009, IEEE Computer Soc.. Los Alamitos, CA, 2009, pp. 324–330. https://doi.org/10.1109/FOCS.2009.25Google Scholar
Andoni, A., Indyk, P., and Krauthgamer, R., Earth mover distance over high-dimensional spaces. In: Proceedings of the Nineteenth Annual ACM-SIAM Symposium on Discrete Algorithms. ACM, New York, 2008, pp. 343–352.Google Scholar
Andoni, A., Naor, A., and Neiman, O., Snowflake universality of Wasserstein spaces. Ann. Sci. Éc. Norm. Supér. (4) 51(2018), no. 3, 657–700. https://doi.org/10.24033/asens.2363Google Scholar
Andrew, A. D., On subsequences of the Haar system in C (𝛥). Israel J. Math. 31(1978), 85–90. https://doi.org/10.1007/BF02761382Google Scholar
Arens, R. F. and Eells, J. Jr., On embedding uniform and topological spaces. Pacific J. Math. 6(1956), 397–403.Google Scholar
Benyamini, Y. and Lindenstrauss, J., Geometric nonlinear functional analysis. Vol. 1. American Mathematical Society Colloquium Publications, 48, American Mathematical Society, Providence, RI, 2000.Google Scholar
Biggs, N. L., Algebraic potential theory on graphs. Bull. London Math. Soc. 29(1997), no. 6, 641–682. https://doi.org/10.1112/S0024609397003305Google Scholar
Bondy, J. A. and Murty, U. S. R., Graph theory. Graduate Texts in Mathematics, 244, Springer, New York, 2008. https://doi.org/10.1007/978-1-84628-970-5Google Scholar
Bourgain, J., On Lipschitz embedding of finite metric spaces in Hilbert space. Israel J. Math. 52(1985), no. 1–2, 46–52. https://doi.org/10.1007/BF02776078Google Scholar
Bourgain, J., The metrical interpretation of superreflexivity in Banach spaces. Israel J. Math. 56(1986), no. 2, 222–230. https://doi.org/10.1007/BF02766125Google Scholar
Bourgain, J. and Szarek, S. J., The Banach-Mazur distance to the cube and the Dvoretzky-Rogers factorization. Israel J. Math. 62(1988), no. 2, 169–180. https://doi.org/10.1007/BF02787120Google Scholar
Carlsson, G. and Mémoli, F., Characterization, stability and convergence of hierarchical clustering methods. J. Mach. Learn. Res. 11(2010), 1425–1470.Google Scholar
Cúth, M. and Doucha, M., Lipschitz-free spaces over ultrametric spaces. Mediterr. J. Math. 13(2016), no. 4, 1893–1906. https://doi.org/10.1007/s00009-015-0566-7Google Scholar
Cúth, M., Doucha, M., and Wojtaszczyk, P., On the structure of Lipschitz-free spaces. Proc. Amer. Math. Soc. 144 no. 9, 3833–3846. https://doi.org/10.1090/proc/13019Google Scholar
Dalet, A., Free spaces over some proper metric spaces. Mediterr. J. Math. 12(2015), no. 3, 973–986. https://doi.org/10.1007/s00009-014-0455-5Google Scholar
Diestel, R., Graph theory, Fifth ed., Graduate Texts in Mathematics, 173, Springer, Berlin, 2017. https://doi.org/10.1007/978-3-662-53622-3Google Scholar
Dilworth, S. J., Kalton, N. J., and Kutzarova, D., On the existence of almost greedy bases in Banach spaces. Studia Math. 159(2003), 67–101. https://doi.org/10.4064/sm159-1-4Google Scholar
Dilworth, S. J., Kalton, N. J., Kutzarova, D., and Temlyakov, V. N., The thresholding greedy algorithm, greedy basis, and duality. Constr. Approx. 19(2003), no. 4, 575–597. https://doi.org/10.1007/s00365-002-0525-yGoogle Scholar
Dilworth, S. J., Kutzarova, D., and Wojtaszczyk, P., On approximate ℓ 1 systems in Banach spaces. J. Approx. Theory 114(2002), 214–241. https://doi.org/10.1006/jath.2001.3641Google Scholar
Dobrushin, R. L., Definition of a system of random variables by means of conditional distributions. Teor. Veroyatnost. i Primenen. 15(1970), 469–497; English translation: Theor. Probability Appl. 15 (1970), 458–486.Google Scholar
Doust, I., Sánchez, S., and Weston, A., Asymptotic negative type properties of finite ultrametric spaces. J. Math. Anal. Appl. 446(2017), no. 2, 1776–1793. https://doi.org/10.1016/j.jmaa.2016.09.069Google Scholar
Erdős, P. and Pósa, L., On the maximal number of disjoint circuits of a graph. Publ. Math. Debrecen 9(1962), 3–12.Google Scholar
Giannopoulos, A. A., A note on the Banach–Mazur distance to the cube. In: Geometric aspects of functional analysis (Israel, 1992–1994). Oper. Theory Adv. Appl., 77, Birkhäuser, Basel, 1995, pp. 67–73.Google Scholar
Godard, A., Tree metrics and their Lipschitz-free spaces. Proc. Amer. Math. Soc. 138(2010), no. 12, 4311–4320. https://doi.org/10.1090/S0002-9939-2010-10421-5Google Scholar
Godefroy, G., A survey on Lipschitz-free Banach spaces. Comment. Math. 55(2015), no. 2, 89–118. https://doi.org/10.14708/cm.v55i2.1104Google Scholar
Godefroy, G. and Kalton, N. J., Lipschitz-free Banach spaces. Studia Math. 159(2003), no. 1, 121–141. https://doi.org/10.4064/sm159-1-6Google Scholar
Gogyan, S., Greedy algorithm with regard to Haar subsystems. East J. Approx. 11(2005), 221–236.Google Scholar
Grünbaum, B., Projection constants. Trans. Amer. Math. Soc. 95(1960), 451–465. https://doi.org/10.2307/1993567Google Scholar
Gupta, A., Steiner points in tree metrics don’t (really) help. In: Proceedings of the Twelfth Annual ACM-SIAM Symposium on Discrete Algorithms (Washington, DC, 2001). SIAM, Philadelphia, PA, 2001, pp. 220–227.Google Scholar
Gupta, A., Newman, I., Rabinovich, Y., and Sinclair, A., Cuts, trees and ℓ 1-embeddings of graphs. Combinatorica 24(2004), 233–269. https://doi.org/10.1007/s00493-004-0015-xGoogle Scholar
Indyk, P. and Matoušek, J., Low-distortion embeddings of finite metric spaces. In: Handbook of discrete and computational geometry. Chapman and Hall/CRC, Boca Raton, FL, 2004, pp. 177–196.https://doi.org/10.1201/9781420035315Google Scholar
Johnson, W. B. and Schechtman, G., Diamond graphs and super-reflexivity. J. Topol. Anal. 1(2009), no. 2, 177–189. https://doi.org/10.1142/S1793525309000114Google Scholar
Kadets, M. I. and Snobar, M. G., Certain functionals on the Minkowski compactum (Russian). Mat. Zametki 10(1971), 453–457.Google Scholar
Kalton, N. J., The nonlinear geometry of Banach spaces. Rev. Mat. Complut. 21(2008), no. 1, 7–60. https://doi.org/10.5209/rev_REMA.2008.v21.n1.16426Google Scholar
Kantorovich, L. V., On mass transportation (Russian). Doklady Acad. Naus SSSR, (N.S.) 37(1942), 199–201; English transl.: J. Math. Sci. (N. Y.) 133(2006), no. 4, 1381–1382. https://doi.org/10.1007/s10958-006-0049-2Google Scholar
Kantorovich, L. V. and Rubinstein, G. S., On a space of completely additive functions. (Russian). Vestnik Leningrad. Univ. 13(1958), no. 7, 52–59.Google Scholar
Khot, S. and Naor, A., Nonembeddability theorems via Fourier analysis. Math. Ann. 334(2006), 821–852. https://doi.org/10.1007/s00208-005-0745-0Google Scholar
Konyagin, S. V. and Temlyakov, V. N., A remark on greedy approximation in Banach spaces. East. J. Approx. 5(1999), 365–379.Google Scholar
Kruskal, J. B. Jr., On the shortest spanning subtree of a graph and the traveling salesman problem. Proc. Amer. Math. Soc. 7(1956), 48–50. https://doi.org/10.2307/2033241Google Scholar
Laakso, T. J., Ahlfors Q-regular spaces with arbitrary Q > 1 admitting weak Poincare inequality. Geom. Funct. Anal. 10(2000), no. 1, 111–123. https://doi.org/10.1007/s000390050003+1+admitting+weak+Poincare+inequality.+Geom.+Funct.+Anal.+10(2000),+no.+1,+111–123.+https://doi.org/10.1007/s000390050003>Google Scholar
Lang, U. and Plaut, C., Bilipschitz embeddings of metric spaces into space forms. Geom. Dedicata 87(2001), 285–307. https://doi.org/10.1023/A:1012093209450Google Scholar
Lee, J. R. and Raghavendra, P., Coarse differentiation and multi-flows in planar graphs. Discrete Comput. Geom. 43(2010), no. 2, 346–362. https://doi.org/10.1007/s00454-009-9172-4Google Scholar
Lindenstrauss, J. and Tzafriri, L., Classical Banach spaces. I. Sequence spaces. Ergebnisse der Mathematik und ihrer Grenzgebiete, 92, Springer-Verlag, Berlin-New York, 1977.Google Scholar
Linial, N., London, E., and Rabinovich, Y., The geometry of graphs and some of its algorithmic applications. Combinatorica 15(1995), no. 2, 215–245. https://doi.org/10.1007/BF01200757Google Scholar
Martínez-Abejón, A., Odell, E., and Popov, M. M., Some open problems on the classical function space L 1. Mat. Stud 24(2005), 173–191.Google Scholar
Naor, A. and Rabani, Y., On Lipschitz extension from finite subsets. Israel J. Math. 219(2017), no. 1, 115–161. https://doi.org/10.1007/s11856-017-1475-1Google Scholar
Naor, A. and Schechtman, G., Planar Earthmover is not in L 1. SIAM J. Comput. 37(2007), 804–826. https://doi.org/10.1137/05064206X.Google Scholar
Ostrovska, S. and Ostrovskii, M. I., Nonexistence of embeddings with uniformly bounded distortions of Laakso graphs into diamond graphs. Discrete Math. 340(2017), no. 2, 9–17. https://doi.org/10.1016/j.disc.2016.08.003Google Scholar
Ostrovskii, M. I., Metric embeddings: Bilipschitz and coarse embeddings into Banach spaces. de Gruyter Studies in Mathematics, 49, Walter de Gruyter, Berlin, 2013. https://doi.org/10.1515/9783110264012Google Scholar
Ostrovskii, M. I. and Randrianantoanina, B., A new approach to low-distortion embeddings of finite metric spaces into non-superreflexive Banach spaces. J. Funct. Anal. 273(2017), no. 2, 598–651. https://doi.org/10.1016/j.jfa.2017.03.017Google Scholar
Peleg, D., Distributed computing. A locality-sensitive approach. SIAM Monographs on Discrete Mathematics and Applications, 5, Society for Industrial and Applied Mathematics (SIAM), Philadelphia, PA, 2000.Google Scholar
Rudin, W., Projections on invariant subspaces. Proc. Amer. Math. Soc. 13(1962), 429–432. https://doi.org/10.2307/2034952Google Scholar
Szarek, S. J., Spaces with large distance to ℓ ∞n and random matrices. Amer. J. Math. 112(1990), no. 6, 899–942. https://doi.org/10.2307/2374731Google Scholar
Szarek, S. J. and Talagrand, M., An “isomorphic” version of the Sauer-Shelah lemma and the Banach-Mazur distance to the cube. In: Geometric aspects of functional analysis (1987–88). Lecture Notes in Math., 1376, Springer, Berlin, 1989, pp. 105–112.Google Scholar
Tikhomirov, K., On the Banach-Mazur distance to cross-polytope. Adv. Math. 345(2019), 598–617. https://doi.org/10.1016/j.aim.2019.01.013Google Scholar
Vasershtein, L. N., Markov processes over denumerable products of spaces describing large system of automata. Problems of Information Transmission 5(1969), no. 3, 47–52; translated from: Problemy Peredachi Informatsii 5(1969), no. 3, 64–72. https://doi.org/10.1016/s0016-0032(33)90010-1Google Scholar
Villani, C., Topics in optimal transportation. Graduate Studies in Mathematics, 58, American Mathematical Society, Providence, RI, 2003. https://doi.org/10.1007/b12016Google Scholar
Villani, C., Optimal transport: Old and new. Grundlehren der Mathematischen Wissenschaften, 338, Springer-Verlag, Berlin, 2009. https://doi.org/10.1007/978-3-540-71050-9Google Scholar
Weaver, N., Lipschitz algebras. Second ed., World Scientific Publishing Co. Pte. Ltd., Hackensack, NJ, 2018.Google Scholar
Youssef, P., Restricted invertibility and the Banach-Mazur distance to the cube. Mathematika 60(2014), no. 1, 201–218. https://doi.org/10.1112/S0025579313000144Google Scholar