Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kubokawa, Yoshihiro
1972.
A general local ergodic theorem.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 48,
Issue. 7,
Kubokawa, Yoshihiro
1974.
A local ergodic theorem for semi-group on $L_{p}$.
Tohoku Mathematical Journal,
Vol. 26,
Issue. 3,
Baxter, J. R.
and
Chacon, R. V.
1974.
A Local Ergodic Theorem on Lp.
Canadian Journal of Mathematics,
Vol. 26,
Issue. 5,
p.
1206.
Katok, A. B.
Sinai, Ya. G.
and
Stepin, A. M.
1977.
Theory of dynamical systems and general transformation groups with invariant measure.
Journal of Soviet Mathematics,
Vol. 7,
Issue. 6,
p.
974.
Akcoglu, Mustafa A.
and
Krengel, Ulrich
1978.
A differentiation theorem for additive processes.
Mathematische Zeitschrift,
Vol. 163,
Issue. 2,
p.
199.
Akcoglu, Mustafa A.
and
Krengel, Ulrich
1979.
A differentiation theorem inL p.
Mathematische Zeitschrift,
Vol. 169,
Issue. 1,
p.
31.
McGrath, S. A.
1980.
Local ergodic theorems for noncommuting semigroups.
Proceedings of the American Mathematical Society,
Vol. 79,
Issue. 2,
p.
212.
Lin, Michael
1982.
On local ergodic convergence of semi-groups and additive processes.
Israel Journal of Mathematics,
Vol. 42,
Issue. 4,
p.
300.
Akcoglu, M. A.
1983.
Measure Theory and its Applications.
Vol. 1033,
Issue. ,
p.
1.
Kataoka, T.
Sato, R.
and
Suzuki, H.
1987.
Differentiation of superadditive processes inL p.
Acta Mathematica Hungarica,
Vol. 49,
Issue. 1-2,
p.
157.
Zaharopol, Radu
1992.
A ratio ergodic theorem in Archimedean Riesz spaces.
Journal of Mathematical Analysis and Applications,
Vol. 169,
Issue. 2,
p.
562.
Sato, Ryotaro
1998.
Vector Valued Differentiation Theorems for Multiparameter Additive Processes in Lp Spaces.
Positivity,
Vol. 2,
Issue. 1,
p.
1.
Junco, Andrés del
2009.
Encyclopedia of Complexity and Systems Science.
p.
2933.
del Junco, Andrés
2009.
Ergodic Theory.
p.
79.
Junco, Andrés del
2012.
Mathematics of Complexity and Dynamical Systems.
p.
241.
Yoshimoto, Takeshi
2013.
Multiparameter ratio ergodic theorems for semigroups.
Journal of Functional Analysis,
Vol. 265,
Issue. 12,
p.
3104.
Yoshimoto, Takeshi
2018.
Almost everywhere convergence of multiple operator averages for affine semigroups.
Acta Scientiarum Mathematicarum,
Vol. 84,
Issue. 3-4,
p.
509.
Bogachev, V. I.
2020.
Non-uniform Kozlov–Treschev averagings in the ergodic theorem.
Russian Mathematical Surveys,
Vol. 75,
Issue. 3,
p.
393.
Bogachev, Vladimir Igorevich
2020.
Неравномерные усреднения Козлова-Трещева в эргодической теореме.
Успехи математических наук,
Vol. 75,
Issue. 3(453),
p.
3.

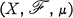 . We denote the integral ∫
. We denote the integral ∫