No CrossRef data available.
Article contents
Local Solvability of Laplacian Difference Operators Arising from the Discrete Heisenberg Group
Published online by Cambridge University Press: 20 November 2018
Abstract
Differential operators 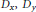 ${{D}_{x,}}\,{{D}_{y}}$, and
${{D}_{x,}}\,{{D}_{y}}$, and 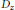 ${{D}_{z}}$ are formed using the action of the 3-dimensional discrete Heisenberg group
${{D}_{z}}$ are formed using the action of the 3-dimensional discrete Heisenberg group  $G$ on a set
$G$ on a set  $S$, and the operators will act on functions on
$S$, and the operators will act on functions on  $S$. The Laplacian operator
$S$. The Laplacian operator 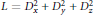 $L\,=\,D_{x}^{2}+D_{y}^{2}+D_{z}^{2}$ is a difference operator with variable differences which can be associated to a unitary representation of
$L\,=\,D_{x}^{2}+D_{y}^{2}+D_{z}^{2}$ is a difference operator with variable differences which can be associated to a unitary representation of  $G$ on the Hilbert space
$G$ on the Hilbert space 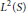 ${{L}^{2}}\left( S \right)$. Using techniques from harmonic analysis and representation theory, we show that the Laplacian operator is locally solvable.
${{L}^{2}}\left( S \right)$. Using techniques from harmonic analysis and representation theory, we show that the Laplacian operator is locally solvable.
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2005


