No CrossRef data available.
Published online by Cambridge University Press: 09 January 2025
In this paper, we investigate locally finitely presented pure semisimple (hereditary) Grothendieck categories. We show that every locally finitely presented pure semisimple (resp., hereditary) Grothendieck category  $\mathscr {A}$ is equivalent to the category of left modules over a left pure semisimple (resp., left hereditary) ring when
$\mathscr {A}$ is equivalent to the category of left modules over a left pure semisimple (resp., left hereditary) ring when  $\mathrm {Mod}(\mathrm {fp}(\mathscr {A}))$ is a QF-3 category, and every representable functor in
$\mathrm {Mod}(\mathrm {fp}(\mathscr {A}))$ is a QF-3 category, and every representable functor in 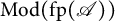 $\mathrm {Mod}(\mathrm {fp}(\mathscr {A}))$ has finitely generated essential socle. In fact, we show that there exists a bijection between Morita equivalence classes of left pure semisimple (resp., left hereditary) rings
$\mathrm {Mod}(\mathrm {fp}(\mathscr {A}))$ has finitely generated essential socle. In fact, we show that there exists a bijection between Morita equivalence classes of left pure semisimple (resp., left hereditary) rings  $\Lambda $ and equivalence classes of locally finitely presented pure semisimple (resp., hereditary) Grothendieck categories
$\Lambda $ and equivalence classes of locally finitely presented pure semisimple (resp., hereditary) Grothendieck categories 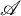 $\mathscr {A}$ that
$\mathscr {A}$ that  $\mathrm {Mod}(\mathrm {fp}(\mathscr {A}))$ is a QF-3 category, and every representable functor in
$\mathrm {Mod}(\mathrm {fp}(\mathscr {A}))$ is a QF-3 category, and every representable functor in 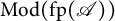 $\mathrm {Mod}(\mathrm {fp}(\mathscr {A}))$ has finitely generated essential socle. To prove this result, we study left pure semisimple rings by using Auslander’s ideas. We show that there exists, up to equivalence, a bijection between the class of left pure semisimple rings and the class of rings with nice homological properties. These results extend the Auslander and Ringel–Tachikawa correspondence to the class of left pure semisimple rings. As a consequence, we give several equivalent statements to the pure semisimplicity conjecture.
$\mathrm {Mod}(\mathrm {fp}(\mathscr {A}))$ has finitely generated essential socle. To prove this result, we study left pure semisimple rings by using Auslander’s ideas. We show that there exists, up to equivalence, a bijection between the class of left pure semisimple rings and the class of rings with nice homological properties. These results extend the Auslander and Ringel–Tachikawa correspondence to the class of left pure semisimple rings. As a consequence, we give several equivalent statements to the pure semisimplicity conjecture.
The research of the first author was in part supported by a grant from IPM. Also, the research of the second author was in part supported by a grant from IPM (No. 1403160416). The work of the second author is based upon research funded by Iran National Science Foundation (INSF) under project No. 4001480.
Dedicated to the memory of Daniel Simson