Article contents
Lorentz Estimates for Weak Solutions of Quasi-linear Parabolic Equations with Singular Divergence-free Drifts
Published online by Cambridge University Press: 07 January 2019
Abstract
This paper investigates regularity in Lorentz spaces for weak solutions of a class of divergence form quasi-linear parabolic equations with singular divergence-free drifts. In this class of equations, the principal terms are vector field functions that are measurable in (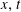 $x,t$)-variable, and nonlinearly dependent on both unknown solutions and their gradients. Interior, local boundary, and global regularity estimates in Lorentz spaces for gradients of weak solutions are established assuming that the solutions are in BMO space, the John–Nirenberg space. The results are even new when the drifts are identically zero, because they do not require solutions to be bounded as in the available literature. In the linear setting, the results of the paper also improve the standard Calderón–Zygmund regularity theory to the critical borderline case. When the principal term in the equation does not depend on the solution as its variable, our results recover and sharpen known available results. The approach is based on the perturbation technique introduced by Caffarelli and Peral together with a “double-scaling parameter” technique and the maximal function free approach introduced by Acerbi and Mingione.
$x,t$)-variable, and nonlinearly dependent on both unknown solutions and their gradients. Interior, local boundary, and global regularity estimates in Lorentz spaces for gradients of weak solutions are established assuming that the solutions are in BMO space, the John–Nirenberg space. The results are even new when the drifts are identically zero, because they do not require solutions to be bounded as in the available literature. In the linear setting, the results of the paper also improve the standard Calderón–Zygmund regularity theory to the critical borderline case. When the principal term in the equation does not depend on the solution as its variable, our results recover and sharpen known available results. The approach is based on the perturbation technique introduced by Caffarelli and Peral together with a “double-scaling parameter” technique and the maximal function free approach introduced by Acerbi and Mingione.
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2018
Footnotes
This research is supported by the Simons Foundation, grant #354889
References
- 1
- Cited by


