Hostname: page-component-745bb68f8f-grxwn Total loading time: 0 Render date: 2025-01-27T11:26:02.631Z Has data issue: false hasContentIssue false
  • English
  • Français

Lower Bounds for the Essential Spectrum of Fourth-Order Differential Operators

Published online by Cambridge University Press:  20 November 2018

Kurt Kreith
Kurt Kreith*
Affiliation:
University of California, Davis, California
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we seek to determine the greatest lower bound of the essential spectrum of self-adjoint singular differential operators of the form

1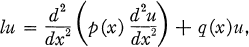

where 0 ≦ x < ∞. In the event that this bound is + ∞, our results will yield criteria for the discreteness of the spectrum of (1).

Such bounds have been established by Friedrichs (3) for Sturm-Liouville operators of the form

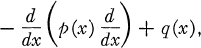
and our techniques will be closely related to those of (3). However, instead of studying the solutions of

2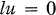

directly, we shall exploit the intimate connection between the infimum of the essential spectrum of (1) and the oscillation properties of (2).

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 21 , 1969 , pp. 460 - 465
Copyright
Copyright © Canadian Mathematical Society 1969

References

1. Akhiezer, N. I. and Glazman, I. M., Theory of linear operators in Hilbert space, Vol. II (Ungar, New York, 1963).Google Scholar
2. Dunford, N. and Schwartz, J., Linear operators, Part II (Interscience, New York, 1963).Google Scholar
3. Friedrichs, K. O., Criteria for discrete spectra, Comm. Pure Appl. Math. 3 (1950), 439–449.Google Scholar
4. Hinton, D., Clamped end boundary conditions for fourth-order self-adjoint differential equations, Duke Math. J. 44 (1967), 131–138.Google Scholar
5. Howard, H., Oscillation criteria for fourth-order linear differential equations, Trans. Amer. Math. Soc. 96 (1960), 296–311.Google Scholar
6. Kreith, K., An abstract oscillation theorem, Proc. Amer. Math. Soc. 19 (1968), 17–20.Google Scholar
7. Leighton, W. and Nehari, Z., On the oscillation of solutions of self-adjoint linear differential equations of fourth order, Trans. Amer. Math. Soc. 89 (1958), 325–377.Google Scholar
8. Riesz, F. and -Nagy, B. Sz., Functional analysis (Ungar, New York, 1955).Google Scholar