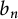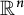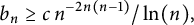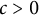1 Introduction
An outstanding problem on the boundary behavior of harmonic functions in space is to identify the maximal minimal dimension of a subset of the boundary of a domain through which Brownian motion first exits the domain almost surely [Reference Bishop8]. Adopting the parlance of geometric measure theory [Reference Falconer13, Reference Mattila, Morán and Rey25], one would like to identify the largest possible (upper) Hausdorff dimension
![]() $\overline {\dim }_H\,\omega $
of harmonic measure
$\overline {\dim }_H\,\omega $
of harmonic measure
![]() $\omega =\omega _\Omega $
across all connected, open sets
$\omega =\omega _\Omega $
across all connected, open sets
![]() $\Omega \subsetneq \mathbb {R}^n$
. For planar domains (
$\Omega \subsetneq \mathbb {R}^n$
. For planar domains (
![]() $n=2$
), the Hausdorff dimension of harmonic measure is at most
$n=2$
), the Hausdorff dimension of harmonic measure is at most
![]() $1$
[Reference Jones and Wolff19] (see also [Reference Carleson11, Reference Kaufman and Jang-Mei20, Reference Makarov23, Reference Øksendal27, Reference Wolff29]) and this is sharp (e.g., when
$1$
[Reference Jones and Wolff19] (see also [Reference Carleson11, Reference Kaufman and Jang-Mei20, Reference Makarov23, Reference Øksendal27, Reference Wolff29]) and this is sharp (e.g., when
![]() $\Omega $
is a disk). For space domains (
$\Omega $
is a disk). For space domains (
![]() $n\geq 3$
), the Hausdorff dimension of harmonic measure is at most
$n\geq 3$
), the Hausdorff dimension of harmonic measure is at most
![]() $n-b_n$
for some undetermined value
$n-b_n$
for some undetermined value
![]() $0<b_n<1$
[Reference Bourgain10, Reference Wolff30] (see also [Reference Lewis, Verchota and Vogel21]), which we call Bourgain’s constant. Determining the value of Bourgain’s constant is related to understanding certain physical phenomenon (passivation, fouling, and poisoning) [Reference Filoche, Grebenkov, Andrade and Sapoval14]. While a conjectural best value
$0<b_n<1$
[Reference Bourgain10, Reference Wolff30] (see also [Reference Lewis, Verchota and Vogel21]), which we call Bourgain’s constant. Determining the value of Bourgain’s constant is related to understanding certain physical phenomenon (passivation, fouling, and poisoning) [Reference Filoche, Grebenkov, Andrade and Sapoval14]. While a conjectural best value
![]() $1/(n-1)$
for
$1/(n-1)$
for
![]() $b_n$
has been proposed [Reference Bishop7], there appears to have been little progress in affirming or disproving this conjecture to date. A numerical experiment [Reference Grebenkov, Lebedev, Filoche and Sapoval16] suggests that
$b_n$
has been proposed [Reference Bishop7], there appears to have been little progress in affirming or disproving this conjecture to date. A numerical experiment [Reference Grebenkov, Lebedev, Filoche and Sapoval16] suggests that
![]() $b_3\leq 0.995$
, but this bound has not been mathematically verified.
$b_3\leq 0.995$
, but this bound has not been mathematically verified.
Very recently, the authors proved an analogue of Bourgain’s theorem in the setting of the heat equation [Reference Badger and Genschaw4]. In particular, the Hausdorff dimension of caloric measure on any domain in
![]() $\mathbb {R}^n\times \mathbb {R}$
(space
$\mathbb {R}^n\times \mathbb {R}$
(space
![]() $\times $
time) with the parabolic distance is at most
$\times $
time) with the parabolic distance is at most
![]() $n+2-\beta _n$
for some
$n+2-\beta _n$
for some
![]() $\beta _n>0$
; moreover,
$\beta _n>0$
; moreover,
![]() $\beta _n\leq b_n$
for all n. (Thus, we indirectly obtain
$\beta _n\leq b_n$
for all n. (Thus, we indirectly obtain
![]() $b_n>0$
.) In the process of establishing this extension, the authors initially had some difficulty implementing the demonstration of
$b_n>0$
.) In the process of establishing this extension, the authors initially had some difficulty implementing the demonstration of
![]() $b_3>0$
from [Reference Bourgain10] in general dimensions.Footnote
1
One goal of this paper is to record a complete and direct proof that
$b_3>0$
from [Reference Bourgain10] in general dimensions.Footnote
1
One goal of this paper is to record a complete and direct proof that
![]() $b_n>0$
when
$b_n>0$
when
![]() $n\geq 3$
. Further, by refining Bourgain’s original outline, we provide quantitative lower bounds on
$n\geq 3$
. Further, by refining Bourgain’s original outline, we provide quantitative lower bounds on
![]() $b_n$
for arbitrary
$b_n$
for arbitrary
![]() $n\geq 3$
and the first explicit numerical lower bounds on
$n\geq 3$
and the first explicit numerical lower bounds on
![]() $b_n$
in dimensions
$b_n$
in dimensions
![]() $n=3,4$
.
$n=3,4$
.
Theorem 1.1 There exists
![]() $c>0$
such that
$c>0$
such that
![]() $b_n\geq c\,n^{-2n(n-1)}/\ln (n)$
for all
$b_n\geq c\,n^{-2n(n-1)}/\ln (n)$
for all
![]() $n\geq 3$
.
$n\geq 3$
.
Theorem 1.2 (15 decimals, 26 decimals)
We have
![]() $b_3\geq 1\times 10^{-15}$
and
$b_3\geq 1\times 10^{-15}$
and
![]() $b_4\geq 2\times 10^{-26}$
. That is to say, the Hausdorff dimension of harmonic measure in
$b_4\geq 2\times 10^{-26}$
. That is to say, the Hausdorff dimension of harmonic measure in
![]() $\mathbb {R}^3$
is at most
$\mathbb {R}^3$
is at most
The Hausdorff dimension of harmonic measure in
![]() $\mathbb {R}^4$
is at most
$\mathbb {R}^4$
is at most
Bourgain’s underlying idea to prove estimates of this type is that if the boundary of a domain is spread uniformly in space throughout a cube, then the probability that a Brownian traveler exits the domain near the center of the cube should be smaller than the probability of exiting the domain near the boundary of the cube. This sets up an alternative: inside any window, either the boundary of the domain is geometrically small at the resolution of the window, or the boundary of the domain is geometrically large, but then we can find a geometrically smaller subset of the boundary that carries most of the harmonic measure. To be more precise, at every m-adic location, for some integer
![]() $m\gg _n 3$
, either the boundary has small
$m\gg _n 3$
, either the boundary has small
![]() $(n-\rho )$
-dimensional content for some
$(n-\rho )$
-dimensional content for some
![]() $0<\rho \ll _{m,n} 1$
or the harmonic measure has positive
$0<\rho \ll _{m,n} 1$
or the harmonic measure has positive
![]() $(n-\lambda )$
-dimensional density on a subset of positive measure for some
$(n-\lambda )$
-dimensional density on a subset of positive measure for some
![]() $0<\lambda \ll _{m,n} 1$
. It follows that
$0<\lambda \ll _{m,n} 1$
. It follows that
(see Lemma 2.2). This approach exhibits strong dimension dependence in the form of volume concentration near the boundary of balls or cubes in high dimensions. In several places, the arguments in [Reference Badger and Genschaw4, Reference Bourgain10] use continuity and soft analysis to assert the existence of the parameters m,
![]() $\rho $
, and
$\rho $
, and
![]() $\lambda $
to conclude that
$\lambda $
to conclude that
![]() $b_n>0$
and
$b_n>0$
and
![]() $\beta _n>0$
. A challenge in proving Theorem 1.1 is to carry out explicit estimates wherever feasible. For Theorem 1.2, one need only track estimates for a small set of values of m, because
$\beta _n>0$
. A challenge in proving Theorem 1.1 is to carry out explicit estimates wherever feasible. For Theorem 1.2, one need only track estimates for a small set of values of m, because
![]() $\rho \rightarrow 0$
rapidly as
$\rho \rightarrow 0$
rapidly as
![]() $m\rightarrow \infty $
. We remark that the method of proof generates some interesting arithmetic phenomenon (see the nonlinear dependence on size of the m-adic grid in the lower bounds on Bourgain’s constant in Table 1).
$m\rightarrow \infty $
. We remark that the method of proof generates some interesting arithmetic phenomenon (see the nonlinear dependence on size of the m-adic grid in the lower bounds on Bourgain’s constant in Table 1).
In Section 2, we introduce necessary elements from geometric measure theory, including a tight version of Frostman’s lemma for sets in
![]() $\mathbb {R}^n$
of Hausdorff dimension
$\mathbb {R}^n$
of Hausdorff dimension
![]() $s>n-1$
. In Section 3, we revisit and sharpen Bourgain’s estimate on harmonic measure from below in terms of the relative size of the local m-adic net content. We also record some basic estimates on harmonic measure inside nested rectangles. In Section 4, we reduce the problem of finding lower bounds on
$s>n-1$
. In Section 3, we revisit and sharpen Bourgain’s estimate on harmonic measure from below in terms of the relative size of the local m-adic net content. We also record some basic estimates on harmonic measure inside nested rectangles. In Section 4, we reduce the problem of finding lower bounds on
![]() $b_n$
to showing the existence of an admissible set of parameters. Using all of these ingredients, we prove Theorem 1.1 in Section 5 and Theorem 1.2 in Section 6. We end with a brief call for future work in Section 7.
$b_n$
to showing the existence of an admissible set of parameters. Using all of these ingredients, we prove Theorem 1.1 in Section 5 and Theorem 1.2 in Section 6. We end with a brief call for future work in Section 7.
2 Net measures, Hausdorff dimension, and Frostman’s lemma
Background on Hausdorff measures, net measures, and related topics can be found in [Reference Bishop and Peres9, Reference Mattila24, Reference Rogers28]. Let
![]() $\mathbb {R}^n$
be equipped with the standard Euclidean distance, i.e.,
$\mathbb {R}^n$
be equipped with the standard Euclidean distance, i.e.,
![]() $|X-Y|= (\sum _1^n (x_i-y_i)^2)^{1/2}$
for all points
$|X-Y|= (\sum _1^n (x_i-y_i)^2)^{1/2}$
for all points
![]() $X=(x_1,\dots ,x_n)$
and
$X=(x_1,\dots ,x_n)$
and
![]() $Y=(y_1,\dots , y_n)$
. Let
$Y=(y_1,\dots , y_n)$
. Let
![]() $\operatorname{\mathrm{diam}}\nolimits E=\sup \{|X-Y|:X,Y\in E\}$
denote the diameter of
$\operatorname{\mathrm{diam}}\nolimits E=\sup \{|X-Y|:X,Y\in E\}$
denote the diameter of
![]() $E\subset \mathbb {R}^n$
. For each integer
$E\subset \mathbb {R}^n$
. For each integer
![]() $m\geq 2$
, define the system
$m\geq 2$
, define the system
![]() $\Delta ^m(\mathbb {R}^n)$
of half-open m-adic cubes to be all sets Q of the form
$\Delta ^m(\mathbb {R}^n)$
of half-open m-adic cubes to be all sets Q of the form
we say that Q belongs to generation k of
![]() $\Delta ^m(\mathbb {R}^{n})$
and has side length
$\Delta ^m(\mathbb {R}^{n})$
and has side length
![]() $\operatorname{\mathrm{side}}\nolimits Q=m^{-k}$
and volume
$\operatorname{\mathrm{side}}\nolimits Q=m^{-k}$
and volume
![]() $\operatorname{\mathrm{vol}}\nolimits Q=m^{-kn}$
. Note that
$\operatorname{\mathrm{vol}}\nolimits Q=m^{-kn}$
. Note that
![]() $\operatorname{\mathrm{diam}}\nolimits Q=\sqrt {n} \operatorname{\mathrm{side}}\nolimits Q$
for every
$\operatorname{\mathrm{diam}}\nolimits Q=\sqrt {n} \operatorname{\mathrm{side}}\nolimits Q$
for every
![]() $Q\in \Delta ^m(\mathbb {R}^{n})$
.
$Q\in \Delta ^m(\mathbb {R}^{n})$
.
The cubes in each generation of
![]() $\Delta ^m(\mathbb {R}^{n})$
partition
$\Delta ^m(\mathbb {R}^{n})$
partition
![]() $\mathbb {R}^{n}$
. Every cube
$\mathbb {R}^{n}$
. Every cube
![]() $Q\in \Delta ^m(\mathbb {R}^{n})$
of generation k is contained in a unique cube
$Q\in \Delta ^m(\mathbb {R}^{n})$
of generation k is contained in a unique cube
![]() $Q^\uparrow \in \Delta ^m(\mathbb {R}^{n})$
of generation
$Q^\uparrow \in \Delta ^m(\mathbb {R}^{n})$
of generation
![]() $k-1$
; we call
$k-1$
; we call
![]() $Q^\uparrow $
the parent of Q and call Q a child of
$Q^\uparrow $
the parent of Q and call Q a child of
![]() $Q^\uparrow $
. Extending this metaphor, we may refer to the ancestors “above” a cube and descendents “below” a cube. For every
$Q^\uparrow $
. Extending this metaphor, we may refer to the ancestors “above” a cube and descendents “below” a cube. For every
![]() $Q\in \Delta ^m(\mathbb {R}^n)$
,
$Q\in \Delta ^m(\mathbb {R}^n)$
,
![]() $\#\operatorname{\mathsf{Child}}\nolimits (Q)=m^{n}$
and
$\#\operatorname{\mathsf{Child}}\nolimits (Q)=m^{n}$
and
![]() $\operatorname{\mathrm{vol}}\nolimits Q=\sum _{R\in \operatorname{\mathsf{Child}}\nolimits (Q)}\operatorname{\mathrm{vol}}\nolimits R,$
where
$\operatorname{\mathrm{vol}}\nolimits Q=\sum _{R\in \operatorname{\mathsf{Child}}\nolimits (Q)}\operatorname{\mathrm{vol}}\nolimits R,$
where
![]() $\operatorname{\mathsf{Child}}\nolimits (Q)$
is the set of children.
$\operatorname{\mathsf{Child}}\nolimits (Q)$
is the set of children.
Definition 2.1 Fix
![]() $\Delta =\Delta ^m(\mathbb {R}^{n})$
and let
$\Delta =\Delta ^m(\mathbb {R}^{n})$
and let
![]() $s\in [0,\infty )$
. For all
$s\in [0,\infty )$
. For all
![]() $\delta \in (0,\infty ]$
, we define
$\delta \in (0,\infty ]$
, we define
 $$ \begin{align*}\mathcal{M}^s_\delta(E)=\inf\left\{\sum_1^\infty (\operatorname{\mathrm{side}}\nolimits E_i)^s:E\subseteq\bigcup_1^\infty E_i, \operatorname{\mathrm{side}}\nolimits E_i\leq \delta, E_i\in\Delta\right\}\quad\text{for all }E\subset\mathbb{R}^{n};\end{align*} $$
$$ \begin{align*}\mathcal{M}^s_\delta(E)=\inf\left\{\sum_1^\infty (\operatorname{\mathrm{side}}\nolimits E_i)^s:E\subseteq\bigcup_1^\infty E_i, \operatorname{\mathrm{side}}\nolimits E_i\leq \delta, E_i\in\Delta\right\}\quad\text{for all }E\subset\mathbb{R}^{n};\end{align*} $$
we call
![]() $\mathcal {M}^s_\infty $
the s-dimensional net content on
$\mathcal {M}^s_\infty $
the s-dimensional net content on
![]() $\mathbb {R}^{n}$
. We define the s-dimensional net measure on
$\mathbb {R}^{n}$
. We define the s-dimensional net measure on
![]() $\mathbb {R}^{n}$
by
$\mathbb {R}^{n}$
by
![]() $\mathcal {M}^s(E)=\lim _{\delta \downarrow 0} \mathcal {M}^s_\delta (E)$
for all
$\mathcal {M}^s(E)=\lim _{\delta \downarrow 0} \mathcal {M}^s_\delta (E)$
for all
![]() $E\subset \mathbb {R}^{n}$
.
$E\subset \mathbb {R}^{n}$
.
Remark 2.1 The net contents
![]() $\mathcal {M}^s_\infty $
are outer measures on
$\mathcal {M}^s_\infty $
are outer measures on
![]() $\mathbb {R}^n$
and the net measures
$\mathbb {R}^n$
and the net measures
![]() $\mathcal {M}^s$
are Borel regular outer measures on
$\mathcal {M}^s$
are Borel regular outer measures on
![]() $\mathbb {R}^{n}$
. Unlike the Hausdorff measures
$\mathbb {R}^{n}$
. Unlike the Hausdorff measures
![]() $\mathcal {H}^s$
and contents
$\mathcal {H}^s$
and contents
![]() $\mathcal {H}^s_\infty $
, the net measures and net contents are neither translation nor dilation invariant. Of course, for all
$\mathcal {H}^s_\infty $
, the net measures and net contents are neither translation nor dilation invariant. Of course, for all
![]() $n\geq 1$
and
$n\geq 1$
and
![]() $s>0$
, we have
$s>0$
, we have
![]() $\mathcal {H}^s \lesssim _{n} \mathcal {M}^s\lesssim _{n,m} \mathcal {H}^s$
and
$\mathcal {H}^s \lesssim _{n} \mathcal {M}^s\lesssim _{n,m} \mathcal {H}^s$
and
![]() $\mathcal {H}^s_\infty \lesssim _{n} \mathcal {M}^s_\infty \lesssim _{n,m} \mathcal {H}^s_\infty $
. This allows us to define Hausdorff dimension using net measures in lieu of Hausdorff measures. While the net measures and net contents depend on the choice of the underlying grid
$\mathcal {H}^s_\infty \lesssim _{n} \mathcal {M}^s_\infty \lesssim _{n,m} \mathcal {H}^s_\infty $
. This allows us to define Hausdorff dimension using net measures in lieu of Hausdorff measures. While the net measures and net contents depend on the choice of the underlying grid
![]() $\Delta =\Delta ^m(\mathbb {R}^n)$
, for simplicity, we suppress this from the notation. We choose the letter
$\Delta =\Delta ^m(\mathbb {R}^n)$
, for simplicity, we suppress this from the notation. We choose the letter
![]() $\mathcal {M}$
to suggest m-adic. An elementary fact is that
$\mathcal {M}$
to suggest m-adic. An elementary fact is that
![]() $\mathcal {M}^s(E)=0$
if and only if
$\mathcal {M}^s(E)=0$
if and only if
![]() $\mathcal {M}^s_\infty (E)=0$
.
$\mathcal {M}^s_\infty (E)=0$
.
Definition 2.2 Let
![]() $E\subset \mathbb {R}^n$
. The Hausdorff dimension of E is the unique number
$E\subset \mathbb {R}^n$
. The Hausdorff dimension of E is the unique number
![]() $\dim _H E\in [0,n]$
where one witnesses a transition from
$\dim _H E\in [0,n]$
where one witnesses a transition from
![]() $\mathcal {M}^s(E)=\infty $
for all
$\mathcal {M}^s(E)=\infty $
for all
![]() $s<\dim _H E$
to
$s<\dim _H E$
to
![]() $\mathcal {M}^s(E)=0$
for all
$\mathcal {M}^s(E)=0$
for all
![]() $s>\dim _H E$
.
$s>\dim _H E$
.
Definition 2.3 Let
![]() $\mu $
be a Borel measure on
$\mu $
be a Borel measure on
![]() $\mathbb {R}^n$
. The upper Hausdorff dimension of
$\mathbb {R}^n$
. The upper Hausdorff dimension of
![]() $\mu $
is defined to be
$\mu $
is defined to be
![]() $\overline {\dim }_H\,\mu = \inf \{\dim _H E : E\subset \mathbb {R}^n \text { is Borel, } \mu (\mathbb {R}^n\setminus E)=0\}.$
$\overline {\dim }_H\,\mu = \inf \{\dim _H E : E\subset \mathbb {R}^n \text { is Borel, } \mu (\mathbb {R}^n\setminus E)=0\}.$
Lemma 2.2 Fix
![]() $\Delta =\Delta ^m(\mathbb {R}^n)$
. Let
$\Delta =\Delta ^m(\mathbb {R}^n)$
. Let
![]() $\mu $
be a Radon measure on
$\mu $
be a Radon measure on
![]() $\mathbb {R}^{n}$
, and let
$\mathbb {R}^{n}$
, and let
![]() $E\subset \mathbb {R}^{n}$
be a Borel set with
$E\subset \mathbb {R}^{n}$
be a Borel set with
![]() $\mu (\mathbb {R}^{n}\setminus E)=0$
. If there exist constants
$\mu (\mathbb {R}^{n}\setminus E)=0$
. If there exist constants
![]() $0<\rho <n$
and
$0<\rho <n$
and
![]() $\lambda>0$
such that for every
$\lambda>0$
such that for every
![]() $Q\in \Delta $
with
$Q\in \Delta $
with
![]() $\operatorname{\mathrm{side}}\nolimits Q\leq 1$
,
$\operatorname{\mathrm{side}}\nolimits Q\leq 1$
,
or
then
![]() $\overline {\dim }_H\,\mu \leq n-\lambda \rho /(\lambda +\rho )$
.
$\overline {\dim }_H\,\mu \leq n-\lambda \rho /(\lambda +\rho )$
.
Proof
An implicit version of the lemma with the weaker conclusion
![]() $\overline {\dim }_H\,\mu <n$
appears at the end of [Reference Bourgain10, pp. 481–483]. The authors supplied a detailed proof with the indicated upper bound, in the setting of
$\overline {\dim }_H\,\mu <n$
appears at the end of [Reference Bourgain10, pp. 481–483]. The authors supplied a detailed proof with the indicated upper bound, in the setting of
![]() $\mathbb {R}^{n}\times \mathbb {R}$
, equipped with the parabolic distance. For the Euclidean case, simply repeat the proof of [Reference Badger and Genschaw4, Theorem 2.10], making the following superficial change. Replace each occurrence of
$\mathbb {R}^{n}\times \mathbb {R}$
, equipped with the parabolic distance. For the Euclidean case, simply repeat the proof of [Reference Badger and Genschaw4, Theorem 2.10], making the following superficial change. Replace each occurrence of
![]() $n+2$
(the Hausdorff dimension of parabolic
$n+2$
(the Hausdorff dimension of parabolic
![]() $\mathbb {R}^{n}\times \mathbb {R}$
) with n (the Hausdorff dimension of
$\mathbb {R}^{n}\times \mathbb {R}$
) with n (the Hausdorff dimension of
![]() $\mathbb {R}^n$
).
$\mathbb {R}^n$
).
Lemma 2.3 (Frostman’s lemma with better constant)
Fix
![]() $\Delta =\Delta ^m(\mathbb {R}^n)$
. Let
$\Delta =\Delta ^m(\mathbb {R}^n)$
. Let
![]() $K\subset \mathbb {R}^{n}$
be a compact set. If
$K\subset \mathbb {R}^{n}$
be a compact set. If
![]() $s>n-1$
, then there exists a Radon measure
$s>n-1$
, then there exists a Radon measure
![]() $\mu $
on
$\mu $
on
![]() $\mathbb {R}^{n}$
such that
$\mathbb {R}^{n}$
such that
![]() $\mu (Q)\leq (\operatorname{\mathrm{side}}\nolimits Q)^s$
for all
$\mu (Q)\leq (\operatorname{\mathrm{side}}\nolimits Q)^s$
for all
![]() $Q\in \Delta $
,
$Q\in \Delta $
,
![]() $\mu (\partial Q)=0$
for all
$\mu (\partial Q)=0$
for all
![]() $Q\in \Delta $
, and
$Q\in \Delta $
, and
![]() $\mu (\mathbb {R}^n)=\mu (K)\geq \mathcal {M}^s_\infty (K)$
.
$\mu (\mathbb {R}^n)=\mu (K)\geq \mathcal {M}^s_\infty (K)$
.
Remark When
![]() $s>n-1$
, the “constant” in front of
$s>n-1$
, the “constant” in front of
![]() $\mathcal {M}^s_\infty (K)$
is 1. For smaller s, it is possible that
$\mathcal {M}^s_\infty (K)$
is 1. For smaller s, it is possible that
![]() $\mu (\partial Q)>0$
for some
$\mu (\partial Q)>0$
for some
![]() $Q\in \Delta $
and the proof only gives
$Q\in \Delta $
and the proof only gives
![]() $\mu (\mathbb {R}^n)\geq 2^{-n}\mathcal {M}^s_\infty (K)$
. If one would like to relax the requirement that K be compact to K Souslin or to require
$\mu (\mathbb {R}^n)\geq 2^{-n}\mathcal {M}^s_\infty (K)$
. If one would like to relax the requirement that K be compact to K Souslin or to require
![]() $\mu $
satisfy the stronger conclusion
$\mu $
satisfy the stronger conclusion
![]() $\mu (A)\leq (\operatorname{\mathrm{diam}}\nolimits A)^s$
for all sets
$\mu (A)\leq (\operatorname{\mathrm{diam}}\nolimits A)^s$
for all sets
![]() $A\subset \mathbb {R}^n$
, then the constant in front of
$A\subset \mathbb {R}^n$
, then the constant in front of
![]() $\mathcal {M}^s_\infty (K)$
becomes even smaller (see [Reference Mattila24, pp. 112–114]).
$\mathcal {M}^s_\infty (K)$
becomes even smaller (see [Reference Mattila24, pp. 112–114]).
Proof Let
![]() $K\subset \mathbb {R}^n$
be compact and fix
$K\subset \mathbb {R}^n$
be compact and fix
![]() $s>n-1$
. We will modify a standard proof of Frostman’s lemma, exploiting the fact that s is greater than the Hausdorff dimension of the boundaries of m-adic cubes. Cover K with a finite list of cubes
$s>n-1$
. We will modify a standard proof of Frostman’s lemma, exploiting the fact that s is greater than the Hausdorff dimension of the boundaries of m-adic cubes. Cover K with a finite list of cubes
![]() $Q_1,\dots ,Q_l\in \Delta $
with the property that each pair
$Q_1,\dots ,Q_l\in \Delta $
with the property that each pair
![]() $Q_i$
and
$Q_i$
and
![]() $Q_j$
have no common ancestors unless
$Q_j$
have no common ancestors unless
![]() $i=j$
. Then
$i=j$
. Then
![]() $\mathcal {M}^s_\infty (K)=\sum _{i=1}^l \mathcal {M}^s_\infty (K\cap Q_i)$
. Suppose that for each i, we can construct a Radon measure
$\mathcal {M}^s_\infty (K)=\sum _{i=1}^l \mathcal {M}^s_\infty (K\cap Q_i)$
. Suppose that for each i, we can construct a Radon measure
![]() $\mu _i$
on
$\mu _i$
on
![]() $\mathbb {R}^{n}$
such that
$\mathbb {R}^{n}$
such that
![]() $\mu _i(Q)\leq (\operatorname{\mathrm{side}}\nolimits Q)^s$
for all
$\mu _i(Q)\leq (\operatorname{\mathrm{side}}\nolimits Q)^s$
for all
![]() $Q\in \Delta $
,
$Q\in \Delta $
,
![]() $\mu _i(\partial Q)=0$
for all
$\mu _i(\partial Q)=0$
for all
![]() $Q\in \Delta $
, and
$Q\in \Delta $
, and
![]() $\mu _i(\mathbb {R}^n)=\mu _i(K\cap \overline {Q}_i)\geq \mathcal {M}^s_\infty (K\cap Q_i)$
. (See the next paragraph.) Then
$\mu _i(\mathbb {R}^n)=\mu _i(K\cap \overline {Q}_i)\geq \mathcal {M}^s_\infty (K\cap Q_i)$
. (See the next paragraph.) Then
![]() $\mu =\mu _1+\cdots +\mu _l$
is our desired measure, because each
$\mu =\mu _1+\cdots +\mu _l$
is our desired measure, because each
![]() $\mu _i$
vanishes on the boundaries of cubes in
$\mu _i$
vanishes on the boundaries of cubes in
![]() $\Delta $
and pairwise
$\Delta $
and pairwise
![]() $Q_1,\dots , Q_l$
have no common ancestors.
$Q_1,\dots , Q_l$
have no common ancestors.
Fix a cube
![]() $Q_0\in \Delta $
and assign
$Q_0\in \Delta $
and assign
![]() $E:=K\cap Q_0\subset Q_0$
. Following the proof of [Reference Mattila24, Theorem 8.8], using m-adic cubes instead of dyadic cubes, one may produce a sequence of Radon measure
$E:=K\cap Q_0\subset Q_0$
. Following the proof of [Reference Mattila24, Theorem 8.8], using m-adic cubes instead of dyadic cubes, one may produce a sequence of Radon measure
![]() $(\nu _k)_{k=1}^\infty $
such that:
$(\nu _k)_{k=1}^\infty $
such that:
-
(1) the support of
 $\nu _k$
belongs to the closure of
$\nu _k$
belongs to the closure of
 $\bigcup \{Q\in \Delta : \operatorname{\mathrm{side}}\nolimits Q = m^{-k},\; Q\cap E\neq \emptyset \}$
;
$\bigcup \{Q\in \Delta : \operatorname{\mathrm{side}}\nolimits Q = m^{-k},\; Q\cap E\neq \emptyset \}$
; -
(2)
 $\nu _k(\partial Q)=0$
for all
$\nu _k(\partial Q)=0$
for all
 $Q\in \Delta $
;
$Q\in \Delta $
; -
(3)
 $\nu _k(Q)\leq (\operatorname{\mathrm{side}}\nolimits Q)^s$
for all
$\nu _k(Q)\leq (\operatorname{\mathrm{side}}\nolimits Q)^s$
for all
 $Q\in \Delta $
with
$Q\in \Delta $
with
 $\operatorname{\mathrm{side}}\nolimits Q\geq m^{-k}$
; and
$\operatorname{\mathrm{side}}\nolimits Q\geq m^{-k}$
; and -
(4) for each
 $X\in E$
, there is
$X\in E$
, there is
 $Q^X\in \Delta $
with
$Q^X\in \Delta $
with
 $\operatorname{\mathrm{side}}\nolimits Q^X\geq m^{-k}$
and
$\operatorname{\mathrm{side}}\nolimits Q^X\geq m^{-k}$
and
 $\nu _k(Q^X)=(\operatorname{\mathrm{side}}\nolimits Q^X)^s$
.
$\nu _k(Q^X)=(\operatorname{\mathrm{side}}\nolimits Q^X)^s$
.
By (1)–(3),
![]() $\nu _k(\mathbb {R}^n)=\nu _k(\overline {Q_0})=\nu _k(Q_0)\leq (\operatorname{\mathrm{side}}\nolimits Q_0)^s<\infty $
for all k that are large enough so that
$\nu _k(\mathbb {R}^n)=\nu _k(\overline {Q_0})=\nu _k(Q_0)\leq (\operatorname{\mathrm{side}}\nolimits Q_0)^s<\infty $
for all k that are large enough so that
![]() $\operatorname{\mathrm{side}}\nolimits Q_0 \geq m^{-k}$
. By weak compactness of Radon measures, there exist a subsequence
$\operatorname{\mathrm{side}}\nolimits Q_0 \geq m^{-k}$
. By weak compactness of Radon measures, there exist a subsequence
![]() $(\nu _{k_j})_{j=1}^\infty $
and a Radon measure
$(\nu _{k_j})_{j=1}^\infty $
and a Radon measure
![]() $\nu $
such that
$\nu $
such that
![]() $\nu _{k_j}$
converges weakly to
$\nu _{k_j}$
converges weakly to
![]() $\nu $
as
$\nu $
as
![]() $j\rightarrow \infty $
in the sense of Radon measures. By (1), the support of
$j\rightarrow \infty $
in the sense of Radon measures. By (1), the support of
![]() $\nu $
is contained in
$\nu $
is contained in
![]() $K\cap \overline {Q_0}$
. By (4), for each k, there exist (maximal) disjoint cubes
$K\cap \overline {Q_0}$
. By (4), for each k, there exist (maximal) disjoint cubes
![]() $Q^{X_1},\dots , Q^{X_p}$
such that
$Q^{X_1},\dots , Q^{X_p}$
such that
![]() $E\subset Q^{X_1}\cup \dots \cup Q^{X_p}$
and
$E\subset Q^{X_1}\cup \dots \cup Q^{X_p}$
and
![]() $\nu _k(\mathbb {R}^n)\geq \sum _{i=1}^p \nu _k(Q^{X_i}) = \sum _{i=1}^p (\operatorname{\mathrm{side}}\nolimits Q^{X_i})^s \geq \mathcal {M}^s_\infty (E)$
. Thus,
$\nu _k(\mathbb {R}^n)\geq \sum _{i=1}^p \nu _k(Q^{X_i}) = \sum _{i=1}^p (\operatorname{\mathrm{side}}\nolimits Q^{X_i})^s \geq \mathcal {M}^s_\infty (E)$
. Thus,
Next, let
![]() $Q\in \Delta $
. For all
$Q\in \Delta $
. For all
![]() $i\geq 1$
, a sufficiently small open neighborhood of
$i\geq 1$
, a sufficiently small open neighborhood of
![]() $\partial Q$
can be covered by
$\partial Q$
can be covered by
![]() $C(n) m^{i(n-1)}$
cubes
$C(n) m^{i(n-1)}$
cubes
![]() $R\in \Delta $
with
$R\in \Delta $
with
![]() $\operatorname{\mathrm{side}}\nolimits R = m^{-i}\operatorname{\mathrm{side}}\nolimits Q$
. By (3), it follows that
$\operatorname{\mathrm{side}}\nolimits R = m^{-i}\operatorname{\mathrm{side}}\nolimits Q$
. By (3), it follows that
Hence,
![]() $\nu (\partial Q)=0$
, since
$\nu (\partial Q)=0$
, since
![]() $s>n-1$
. Consequently,
$s>n-1$
. Consequently,
![]() $\nu (Q)=\lim _{j\rightarrow \infty } \nu _{k_j}(Q) \leq (\operatorname{\mathrm{side}}\nolimits Q)^s$
.
$\nu (Q)=\lim _{j\rightarrow \infty } \nu _{k_j}(Q) \leq (\operatorname{\mathrm{side}}\nolimits Q)^s$
.
3 Estimates for harmonic measure
Harmonic measure is perhaps best viewed through several complementary perspectives, including geometric function theory [Reference Garnett and Marshall15], potential theory [Reference Helms17], and stochastic processes [Reference Mörters and Peres26]. To ease notation, we adopt the following convention. Domains are assumed to be connected open sets. On a bounded domain
![]() $\Omega \subset \mathbb {R}^n$
, we let
$\Omega \subset \mathbb {R}^n$
, we let
![]() $\partial \Omega $
denote the topological boundary in the Euclidean topology. On an unbounded domain
$\partial \Omega $
denote the topological boundary in the Euclidean topology. On an unbounded domain
![]() $\Omega \subset \mathbb {R}^n$
, we let
$\Omega \subset \mathbb {R}^n$
, we let
![]() $\partial \Omega $
denote the topological boundary in a one-point compactification of
$\partial \Omega $
denote the topological boundary in a one-point compactification of
![]() $\Omega $
so that
$\Omega $
so that
![]() $\partial \Omega $
includes the point at infinity. This ensures that for any domain
$\partial \Omega $
includes the point at infinity. This ensures that for any domain
![]() $\Omega \subsetneq \mathbb {R}^n$
,
$\Omega \subsetneq \mathbb {R}^n$
,
![]() $n\geq 3$
, harmonic measure
$n\geq 3$
, harmonic measure
![]() $\omega ^X_\Omega $
with pole at
$\omega ^X_\Omega $
with pole at
![]() $X\in \Omega $
exists and is a Borel probability measure with support in
$X\in \Omega $
exists and is a Borel probability measure with support in
![]() $\partial \Omega $
. By Harnack’s inequality,
$\partial \Omega $
. By Harnack’s inequality,
![]() $\omega ^X_\Omega $
and
$\omega ^X_\Omega $
and
![]() $\omega ^Y_\Omega $
are mutually absolutely continuous for all
$\omega ^Y_\Omega $
are mutually absolutely continuous for all
![]() $X,Y\in \Omega $
. In particular, the support and Hausdorff dimension of
$X,Y\in \Omega $
. In particular, the support and Hausdorff dimension of
![]() $\omega ^X_{\Omega }$
are independent of the choice of X.
$\omega ^X_{\Omega }$
are independent of the choice of X.
Given an m-adic grid
![]() $\Delta =\Delta ^m(\mathbb {R}^n)$
, we let
$\Delta =\Delta ^m(\mathbb {R}^n)$
, we let
denote the set of translates of m-adic cubes that are aligned with m-adic cubes of the next generation. The following lemma is modeled after [Reference Bourgain10, Lemma 1]. Results of this type are now collectively referred to as Bourgain’s estimate and have become a fundamental tool used to study absolute continuity of harmonic measure (see, e.g., [Reference Azzam, Hofmann, Martell, Mayboroda, Mourgoglou, Tolsa and Volberg3, Reference Hofmann and Martell18]). Also, see [Reference Azzam2, Reference Batakis5, Reference Batakis and Zdunik6] for applications of Bourgain’s estimate to study the dimension of harmonic measure on special classes of domains.
Lemma 3.1 (Bourgain’s estimate with better constants)
Fix
![]() $\Delta =\Delta ^m(\mathbb {R}^n)$
for some
$\Delta =\Delta ^m(\mathbb {R}^n)$
for some
![]() $n\geq 3$
and
$n\geq 3$
and
![]() $m\geq 5$
with
$m\geq 5$
with
![]() $m>\xi _m+2\sqrt {n}$
, where we define
$m>\xi _m+2\sqrt {n}$
, where we define
![]() $\xi _m:=1$
, when m is odd, and
$\xi _m:=1$
, when m is odd, and
![]() $\xi _m:=2$
, when m is even. Let
$\xi _m:=2$
, when m is even. Let
![]() $P\in \vec {\Delta }$
and
$P\in \vec {\Delta }$
and
![]() $P_*\in \Delta $
be any cubes such that
$P_*\in \Delta $
be any cubes such that
![]() $\operatorname{\mathrm{side}}\nolimits P_*=m^{-1}\operatorname{\mathrm{side}}\nolimits P$
and
$\operatorname{\mathrm{side}}\nolimits P_*=m^{-1}\operatorname{\mathrm{side}}\nolimits P$
and
![]() $\overline {P_*}$
includes the center of P. Assign
$\overline {P_*}$
includes the center of P. Assign
![]() $Q:=\operatorname{\mathrm{int}}\nolimits {P}$
and
$Q:=\operatorname{\mathrm{int}}\nolimits {P}$
and
![]() $Q_*:=\overline {P_*}$
(Figure 1). For all closed sets
$Q_*:=\overline {P_*}$
(Figure 1). For all closed sets
![]() $E\subset \mathbb {R}^{n}$
, poles
$E\subset \mathbb {R}^{n}$
, poles
![]() $X\in Q_*\setminus E$
, and dimensions
$X\in Q_*\setminus E$
, and dimensions
![]() $n-1<s\leq n$
,
$n-1<s\leq n$
,
 $$ \begin{align} \left(\left(\frac{1}{\sqrt{n}}\right)^{n-2}-\left(\frac{2}{m-\xi_m}\right)^{n-2}\right)\frac{\mathcal{M}^s_\infty(E\cap Q_*)}{(\operatorname{\mathrm{side}}\nolimits Q_*)^s}\leq O(n,m,s)\,\omega^X_{Q\setminus E}(E\cap Q),\end{align} $$
$$ \begin{align} \left(\left(\frac{1}{\sqrt{n}}\right)^{n-2}-\left(\frac{2}{m-\xi_m}\right)^{n-2}\right)\frac{\mathcal{M}^s_\infty(E\cap Q_*)}{(\operatorname{\mathrm{side}}\nolimits Q_*)^s}\leq O(n,m,s)\,\omega^X_{Q\setminus E}(E\cap Q),\end{align} $$
where
 $$ \begin{align} O(n,m,s)=\min_{k\in\mathbb{Z}}\left(\left(\frac{2m^{k}}{(n-2)\sqrt{n}}\right)^{n-2} +\frac{\omega_n}{4} \left(\frac{mn}{n-2}\right)^{n-2}\frac{n^3m^{k(n-2-s)}}{1-m^{n-2-s}}\right).\end{align} $$
$$ \begin{align} O(n,m,s)=\min_{k\in\mathbb{Z}}\left(\left(\frac{2m^{k}}{(n-2)\sqrt{n}}\right)^{n-2} +\frac{\omega_n}{4} \left(\frac{mn}{n-2}\right)^{n-2}\frac{n^3m^{k(n-2-s)}}{1-m^{n-2-s}}\right).\end{align} $$

Figure 1: Examples of
![]() $Q_*$
and Q in Lemma 3.1 when
$Q_*$
and Q in Lemma 3.1 when
![]() $m=5$
(left) and
$m=5$
(left) and
![]() $m=6$
(right). The smaller cube
$m=6$
(right). The smaller cube
![]() $Q_*$
is the closure of a cube
$Q_*$
is the closure of a cube
![]() $P_*\in \Delta ^m(\mathbb {R}^2)$
. The larger cube Q is the interior of a cube
$P_*\in \Delta ^m(\mathbb {R}^2)$
. The larger cube Q is the interior of a cube
![]() $P\in \vec \Delta ^m(\mathbb {R}^2)$
.
$P\in \vec \Delta ^m(\mathbb {R}^2)$
.
Remark. Here and below, we let
![]() $\omega _n$
denote the volume of the unit ball in
$\omega _n$
denote the volume of the unit ball in
![]() $\mathbb {R}^n$
. When m is odd, the cube
$\mathbb {R}^n$
. When m is odd, the cube
![]() $P_*$
is uniquely determined by P. When m is even, there are
$P_*$
is uniquely determined by P. When m is even, there are
![]() $2^n$
possibilities for
$2^n$
possibilities for
![]() $P_*$
for each P. The gap (distance) between
$P_*$
for each P. The gap (distance) between
![]() $P_*$
and
$P_*$
and
![]() $\partial P$
is
$\partial P$
is
![]() $(m-\xi _m)/2$
times
$(m-\xi _m)/2$
times
![]() $\operatorname{\mathrm{side}}\nolimits P_*$
. The value of k that minimizes
$\operatorname{\mathrm{side}}\nolimits P_*$
. The value of k that minimizes
![]() $O(n,m,s)$
depends on n,
$O(n,m,s)$
depends on n,
![]() $\log _n(m)$
, and s.
$\log _n(m)$
, and s.
Proof Let n, m, Q, and
![]() $Q_*$
be given with the stated requirements. Let
$Q_*$
be given with the stated requirements. Let
![]() $E\subset \mathbb {R}^{n}$
be closed. Because
$E\subset \mathbb {R}^{n}$
be closed. Because
![]() $Q_*$
is compact,
$Q_*$
is compact,
![]() $K:=E\cap Q_*$
is compact. Freeze
$K:=E\cap Q_*$
is compact. Freeze
![]() $n-1<s\leq n$
. By Lemma 2.3, there exists a finite Borel measure
$n-1<s\leq n$
. By Lemma 2.3, there exists a finite Borel measure
![]() $\mu $
on
$\mu $
on
![]() $\mathbb {R}^{n}$
with support in K such that
$\mathbb {R}^{n}$
with support in K such that
![]() $\mu (R)\leq (\operatorname{\mathrm{side}}\nolimits R)^s$
for all
$\mu (R)\leq (\operatorname{\mathrm{side}}\nolimits R)^s$
for all
![]() $R\in \Delta $
,
$R\in \Delta $
,
![]() $\mu (\partial R)=0$
for all
$\mu (\partial R)=0$
for all
![]() $R\in \Delta $
, and
$R\in \Delta $
, and
![]() $\mu (\mathbb {R}^n)=\mu (K)\geq \mathcal {M}^s_\infty (K)$
. Consider the harmonic function
$\mu (\mathbb {R}^n)=\mu (K)\geq \mathcal {M}^s_\infty (K)$
. Consider the harmonic function
![]() $u(X)=\int _K |X-Y|^{-(n-2)}\,d\mu (Y)$
defined on
$u(X)=\int _K |X-Y|^{-(n-2)}\,d\mu (Y)$
defined on
![]() $\mathbb {R}^{n}\setminus K$
, which satisfies
$\mathbb {R}^{n}\setminus K$
, which satisfies
 $$ \begin{align} u(X)\leq (\operatorname{\mathrm{gap}}\nolimits(Q_*,\partial Q))^{-(n-2)}\mu(K)=\left(\frac{m-\xi_m}{2}\operatorname{\mathrm{side}}\nolimits Q_*\right)^{-(n-2)}\mu(K)\quad \forall\,X\in\partial Q, \end{align} $$
$$ \begin{align} u(X)\leq (\operatorname{\mathrm{gap}}\nolimits(Q_*,\partial Q))^{-(n-2)}\mu(K)=\left(\frac{m-\xi_m}{2}\operatorname{\mathrm{side}}\nolimits Q_*\right)^{-(n-2)}\mu(K)\quad \forall\,X\in\partial Q, \end{align} $$
where
![]() $\operatorname{\mathrm{gap}}\nolimits (A,B)=\inf _{a\in A}\inf _{b\in B}|a-b|$
denotes the gap between nonempty sets A and B (sometimes referred to as the distance between A and B). Of the three estimates, (E2) and (E3) are straightforward; we delay the proof of (E1) to the end of the lemma. Following [Reference Bourgain10], define an auxiliary harmonic function w on
$\operatorname{\mathrm{gap}}\nolimits (A,B)=\inf _{a\in A}\inf _{b\in B}|a-b|$
denotes the gap between nonempty sets A and B (sometimes referred to as the distance between A and B). Of the three estimates, (E2) and (E3) are straightforward; we delay the proof of (E1) to the end of the lemma. Following [Reference Bourgain10], define an auxiliary harmonic function w on
![]() $\mathbb {R}^{n}\setminus K$
by setting
$\mathbb {R}^{n}\setminus K$
by setting
 $$ \begin{align*}w(X)=\frac{u(X)-\|u\|_{L^\infty(\partial Q)}}{\|u\|_{L^\infty(\mathbb{R}^n\setminus K)}}\quad\text{for all }X\in\mathbb{R}^{n}\setminus K,\end{align*} $$
$$ \begin{align*}w(X)=\frac{u(X)-\|u\|_{L^\infty(\partial Q)}}{\|u\|_{L^\infty(\mathbb{R}^n\setminus K)}}\quad\text{for all }X\in\mathbb{R}^{n}\setminus K,\end{align*} $$
where the norms denote the supremum of the continuous function u on the specified sets. By design,
![]() $w\leq 0$
on
$w\leq 0$
on
![]() $\partial Q$
, w is continuous on
$\partial Q$
, w is continuous on
![]() $\partial Q$
, and
$\partial Q$
, and
![]() $w\leq 1$
on all of
$w\leq 1$
on all of
![]() $\mathbb {R}^n\setminus K$
. Hence,
$\mathbb {R}^n\setminus K$
. Hence,
Thus,
![]() $w(X)\leq \omega ^{X}_{Q\setminus K}(K)\leq \omega ^X_{Q\setminus E}(E\cap Q)$
for every
$w(X)\leq \omega ^{X}_{Q\setminus K}(K)\leq \omega ^X_{Q\setminus E}(E\cap Q)$
for every
![]() $X\in Q\setminus E$
by two applications of the maximum principle. Suppose that
$X\in Q\setminus E$
by two applications of the maximum principle. Suppose that
![]() $X\in Q_*\setminus E=Q_*\setminus K$
. Using (E1) to estimate the denominator in the definition of w and (E2), (E3) to estimate the numerator, we obtain
$X\in Q_*\setminus E=Q_*\setminus K$
. Using (E1) to estimate the denominator in the definition of w and (E2), (E3) to estimate the numerator, we obtain
 $$ \begin{align*} &\omega^X_{Q\setminus E}(Q\cap E)\geq \frac{\left((1/\sqrt{n})^{n-2} - (2/(m-\xi_m))^{n-2}\right)(\operatorname{\mathrm{side}}\nolimits Q_*)^{-(n-2)}\mathcal{M}^s_\infty(K)}{O(n,m,s)\,(\operatorname{\mathrm{side}}\nolimits Q_*)^{s-(n-2)}}. \end{align*} $$
$$ \begin{align*} &\omega^X_{Q\setminus E}(Q\cap E)\geq \frac{\left((1/\sqrt{n})^{n-2} - (2/(m-\xi_m))^{n-2}\right)(\operatorname{\mathrm{side}}\nolimits Q_*)^{-(n-2)}\mathcal{M}^s_\infty(K)}{O(n,m,s)\,(\operatorname{\mathrm{side}}\nolimits Q_*)^{s-(n-2)}}. \end{align*} $$
This is our desired estimate.
It remains to verify (E1), which is the main improvement over the corresponding lemma in [Reference Bourgain10]. We will use an annular decomposition (see Figure 2), but do not guess the geometry of the annuli in advance. Fix
![]() $X\in \mathbb {R}^{n}\setminus K$
and let
$X\in \mathbb {R}^{n}\setminus K$
and let
![]() $j_0$
denote the integer such that
$j_0$
denote the integer such that
![]() $\operatorname{\mathrm{side}}\nolimits Q_*=m^{-j_0}.$
Recall that
$\operatorname{\mathrm{side}}\nolimits Q_*=m^{-j_0}.$
Recall that
![]() $\mu (R)\leq (\operatorname{\mathrm{side}}\nolimits R)^s$
for all
$\mu (R)\leq (\operatorname{\mathrm{side}}\nolimits R)^s$
for all
![]() $R\in \Delta $
. Let
$R\in \Delta $
. Let
![]() $l\in \mathbb {Z}$
and let
$l\in \mathbb {Z}$
and let
![]() $r_l>0$
(depending on l) to be determined. Let
$r_l>0$
(depending on l) to be determined. Let
![]() $h\in \mathbb {Z}$
and write
$h\in \mathbb {Z}$
and write
![]() $K=B^l_{j_0+h}\cup \bigcup _{j=j_0+h}^\infty A_j^l$
, where
$K=B^l_{j_0+h}\cup \bigcup _{j=j_0+h}^\infty A_j^l$
, where
On one hand, we may trivially estimate
![]() $\mu (B^l_{j_0+h})\leq \mu (Q_*)\leq m^{-j_0s}$
. On the other hand, let
$\mu (B^l_{j_0+h})\leq \mu (Q_*)\leq m^{-j_0s}$
. On the other hand, let
![]() $\omega _n$
denote the volume of the unit ball in
$\omega _n$
denote the volume of the unit ball in
![]() $\mathbb {R}^n$
. Then
$\mathbb {R}^n$
. Then
![]() $A_j^l$
is covered by
$A_j^l$
is covered by
![]() $\lfloor \omega _n (r_l m^l+\sqrt {n})^n\rfloor $
or fewer cubes in
$\lfloor \omega _n (r_l m^l+\sqrt {n})^n\rfloor $
or fewer cubes in
![]() $\Delta $
of side length
$\Delta $
of side length
![]() $m^{-(j+l)}$
. (To derive this, let R represent a cube of side length
$m^{-(j+l)}$
. (To derive this, let R represent a cube of side length
![]() $m^{-(j+l)}$
; divide the volume of a ball of radius
$m^{-(j+l)}$
; divide the volume of a ball of radius
![]() $r_lm^{-j}+\operatorname{\mathrm{diam}}\nolimits R$
by the volume of R.) Hence,
$r_lm^{-j}+\operatorname{\mathrm{diam}}\nolimits R$
by the volume of R.) Hence,
![]() $\mu (A_j^l)\leq \omega _n (r_l m^l+\sqrt {n})^n m^{-(j+l)s}$
. Therefore,
$\mu (A_j^l)\leq \omega _n (r_l m^l+\sqrt {n})^n m^{-(j+l)s}$
. Therefore,
 $$ \begin{align*} u(X) &\leq (1/r_l)^{n-2}m^{(n-2)(j_0+h)}\mu (B^l_{j_0+h}) + \sum_{j=j_0+h}^\infty (1/r_l)^{n-2}m^{(n-2)(j+1)} \mu(A_j^l) \\ &\leq (m^{h}/r_l)^{n-2} m^{j_0(n-2-s)} + (m/r_l)^{n-2} \omega_n (r_lm^l+\sqrt{n})^n m^{-ls}\sum_{j=j_0+h}^\infty m^{j(n-2-s)} \\ &\leq \underbrace{\left((m^{h}/r_l)^{n-2} +\omega_n(m/r_l)^{n-2}(r_lm^l+\sqrt{n})^n \frac{m^{-ls+h(n-2-s)}}{1-m^{n-2-s}}\right)}_I(\operatorname{\mathrm{side}}\nolimits Q_*)^{s-(n-2)}.\end{align*} $$
$$ \begin{align*} u(X) &\leq (1/r_l)^{n-2}m^{(n-2)(j_0+h)}\mu (B^l_{j_0+h}) + \sum_{j=j_0+h}^\infty (1/r_l)^{n-2}m^{(n-2)(j+1)} \mu(A_j^l) \\ &\leq (m^{h}/r_l)^{n-2} m^{j_0(n-2-s)} + (m/r_l)^{n-2} \omega_n (r_lm^l+\sqrt{n})^n m^{-ls}\sum_{j=j_0+h}^\infty m^{j(n-2-s)} \\ &\leq \underbrace{\left((m^{h}/r_l)^{n-2} +\omega_n(m/r_l)^{n-2}(r_lm^l+\sqrt{n})^n \frac{m^{-ls+h(n-2-s)}}{1-m^{n-2-s}}\right)}_I(\operatorname{\mathrm{side}}\nolimits Q_*)^{s-(n-2)}.\end{align*} $$
The quantity
![]() $(m/r_l)^{n-2}(r_lm^l+\sqrt {n})^n$
has a unique critical point and is minimized across all
$(m/r_l)^{n-2}(r_lm^l+\sqrt {n})^n$
has a unique critical point and is minimized across all
![]() $r_l>0$
when
$r_l>0$
when
![]() $r_l=((n-2)\sqrt {n})/2m^l$
. Selecting this value yields
$r_l=((n-2)\sqrt {n})/2m^l$
. Selecting this value yields
 $$ \begin{align*} I&=\left(\frac{2m^{h+l}}{(n-2)\sqrt{n}}\right)^{n-2} +\omega_n\left(\frac{2m^{1+l}}{(n-2)\sqrt{n}}\right)^{n-2}\left(\frac{n\sqrt{n}}{2}\right)^n \frac{m^{-ls+h(n-2-s)}}{1-m^{n-2-s}}\\ &=\left(\frac{2m^{h+l}}{(n-2)\sqrt{n}}\right)^{n-2} +\frac{\omega_n}{4} \left(\frac{mn}{n-2}\right)^{n-2}\frac{n^3m^{(h+l)(n-2-s)}}{1-m^{n-2-s}}. \end{align*} $$
$$ \begin{align*} I&=\left(\frac{2m^{h+l}}{(n-2)\sqrt{n}}\right)^{n-2} +\omega_n\left(\frac{2m^{1+l}}{(n-2)\sqrt{n}}\right)^{n-2}\left(\frac{n\sqrt{n}}{2}\right)^n \frac{m^{-ls+h(n-2-s)}}{1-m^{n-2-s}}\\ &=\left(\frac{2m^{h+l}}{(n-2)\sqrt{n}}\right)^{n-2} +\frac{\omega_n}{4} \left(\frac{mn}{n-2}\right)^{n-2}\frac{n^3m^{(h+l)(n-2-s)}}{1-m^{n-2-s}}. \end{align*} $$
Letting
![]() $h+l$
range over arbitrary values
$h+l$
range over arbitrary values
![]() $k\in \mathbb {Z}$
, we arrive at (E1).
$k\in \mathbb {Z}$
, we arrive at (E1).

Figure 2: Annular decomposition used in the proof of (E1).
We use the following two special cases to prove Theorem 1.1.
Corollary 3.2 For all
![]() $n\geq 3$
, there exists
$n\geq 3$
, there exists
![]() $C_n>1$
depending only on n such that for all
$C_n>1$
depending only on n such that for all
![]() $m>\xi _m+2\sqrt {n}$
and
$m>\xi _m+2\sqrt {n}$
and
![]() $n-1<s\leq n$
,
$n-1<s\leq n$
,
Proof In (3.3), take
![]() $k=0$
or
$k=0$
or
![]() $k=1$
.
$k=1$
.
Corollary 3.3 For all
![]() $\delta>0$
, there exists
$\delta>0$
, there exists
![]() $n_\delta \geq 3$
such that if n and m are integers with
$n_\delta \geq 3$
such that if n and m are integers with
![]() $n\geq n_\delta $
and
$n\geq n_\delta $
and
![]() $m\geq \delta n$
, and
$m\geq \delta n$
, and
![]() $n-1/2<s\leq n$
, then
$n-1/2<s\leq n$
, then
Proof Let
![]() $\delta>0$
be given and fix
$\delta>0$
be given and fix
![]() $\epsilon>0$
to be specified below. Suppose that n and m are integers with
$\epsilon>0$
to be specified below. Suppose that n and m are integers with
![]() $n\geq 3$
and
$n\geq 3$
and
![]() $m\geq \delta n$
. Let us agree to write
$m\geq \delta n$
. Let us agree to write
![]() $c_n\sim d_n$
if
$c_n\sim d_n$
if
![]() $c_n$
is asymptotic to
$c_n$
is asymptotic to
![]() $d_n$
as
$d_n$
as
![]() $n\rightarrow \infty $
in the sense that
$n\rightarrow \infty $
in the sense that
![]() $\lim _{n\rightarrow \infty } c_n/d_n = 1$
and further agree to write
$\lim _{n\rightarrow \infty } c_n/d_n = 1$
and further agree to write
![]() $c_n=o(d_n)$
if
$c_n=o(d_n)$
if
![]() $\lim _{n\rightarrow \infty } c_n/d_n=0$
. Using Stirling’s formula for
$\lim _{n\rightarrow \infty } c_n/d_n=0$
. Using Stirling’s formula for
![]() $\Gamma (x)$
(e.g., [Reference Li22]) and
$\Gamma (x)$
(e.g., [Reference Li22]) and
![]() $\omega _n=\pi ^{n/2}/\Gamma (\frac {n}{2}+1)$
(e.g., [Reference Axler, Bourdon and Ramey1, Appendix A]), we see that
$\omega _n=\pi ^{n/2}/\Gamma (\frac {n}{2}+1)$
(e.g., [Reference Axler, Bourdon and Ramey1, Appendix A]), we see that
 $$ \begin{align*}\omega_n\sim \frac{1}{\sqrt{\pi n}} \left(\frac{\sqrt{2\pi e}}{\sqrt{n}}\right)^n=\frac{2\sqrt{\pi}e}{\sqrt{n}^3}\left(\frac{\sqrt{2\pi e}}{\sqrt{n}}\right)^{n-2}.\end{align*} $$
$$ \begin{align*}\omega_n\sim \frac{1}{\sqrt{\pi n}} \left(\frac{\sqrt{2\pi e}}{\sqrt{n}}\right)^n=\frac{2\sqrt{\pi}e}{\sqrt{n}^3}\left(\frac{\sqrt{2\pi e}}{\sqrt{n}}\right)^{n-2}.\end{align*} $$
We also have
![]() $(n/(n-2))^{n-2}\sim e^2$
. Choosing
$(n/(n-2))^{n-2}\sim e^2$
. Choosing
![]() $k=1$
in (3.3), it follows from the noted asymptotic estimates that for sufficiently large n, depending only on
$k=1$
in (3.3), it follows from the noted asymptotic estimates that for sufficiently large n, depending only on
![]() $\epsilon $
,
$\epsilon $
,
 $$ \begin{align*} \frac{O(n,m,s)}{(1+\epsilon)e^2} &\leq \left(\frac{2m}{n\sqrt{n}}\right)^{n-2} + \frac{\sqrt{\pi}e}{2} \sqrt{n}^{3}m^{n-2-s}\left(\frac{m\sqrt{2\pi e}}{\sqrt{n}}\right)^{n-2},\end{align*} $$
$$ \begin{align*} \frac{O(n,m,s)}{(1+\epsilon)e^2} &\leq \left(\frac{2m}{n\sqrt{n}}\right)^{n-2} + \frac{\sqrt{\pi}e}{2} \sqrt{n}^{3}m^{n-2-s}\left(\frac{m\sqrt{2\pi e}}{\sqrt{n}}\right)^{n-2},\end{align*} $$
where the reader may observe that we also absorbed the factor
![]() $(1-m^{n-2-s})^{-1}$
appearing in
$(1-m^{n-2-s})^{-1}$
appearing in
![]() $O(n,m,s)$
into the error on the left-hand side. Because
$O(n,m,s)$
into the error on the left-hand side. Because
![]() $m\geq \delta n$
and
$m\geq \delta n$
and
![]() $-2\leq n-2-s<-3/2$
, the factor
$-2\leq n-2-s<-3/2$
, the factor
![]() $\sqrt {n}^3 m^{n-2-s}=o(\max \{\delta ^{-2},\delta ^{-3/2}\})=o(1)$
. Also,
$\sqrt {n}^3 m^{n-2-s}=o(\max \{\delta ^{-2},\delta ^{-3/2}\})=o(1)$
. Also,
![]() $(2/n)^{n-2} = o(\sqrt {2\pi e}^{\,n-2})$
. Thus, taking n to be sufficiently large depending only on
$(2/n)^{n-2} = o(\sqrt {2\pi e}^{\,n-2})$
. Thus, taking n to be sufficiently large depending only on
![]() $\delta $
and
$\delta $
and
![]() $\epsilon $
, we have
$\epsilon $
, we have
 $$ \begin{align} O(n,m,s) \leq \epsilon(1+\epsilon)e^2\left(\frac{m\sqrt{2\pi e}}{\sqrt{n}}\right)^{n-2}.\end{align} $$
$$ \begin{align} O(n,m,s) \leq \epsilon(1+\epsilon)e^2\left(\frac{m\sqrt{2\pi e}}{\sqrt{n}}\right)^{n-2}.\end{align} $$
Next, because
![]() $m\geq \delta n$
, we can estimate
$m\geq \delta n$
, we can estimate
 $$ \begin{align} \left(\frac{1}{\sqrt{n}}\right)^{n-2}-\left(\frac{2}{m-\xi_m}\right)^{n-2}\geq (1+\epsilon)^{-1}\sqrt{n}^{-(n-2)} \end{align} $$
$$ \begin{align} \left(\frac{1}{\sqrt{n}}\right)^{n-2}-\left(\frac{2}{m-\xi_m}\right)^{n-2}\geq (1+\epsilon)^{-1}\sqrt{n}^{-(n-2)} \end{align} $$
for all sufficiently large n depending only on
![]() $\epsilon $
and
$\epsilon $
and
![]() $\delta $
. Combining (3.2), (3.6), and (3.7), we conclude that for all n sufficiently large depending only on
$\delta $
. Combining (3.2), (3.6), and (3.7), we conclude that for all n sufficiently large depending only on
![]() $\epsilon $
and
$\epsilon $
and
![]() $\delta $
,
$\delta $
,
Specifying that
![]() $\epsilon (1+\epsilon )^2 e^2=\delta $
yields (3.5).
$\epsilon (1+\epsilon )^2 e^2=\delta $
yields (3.5).
We use the next two special cases to prove Theorem 1.2.
Corollary 3.4 Suppose
![]() $n=3$
. For all integers
$n=3$
. For all integers
![]() $m\geq 5$
and dimensions
$m\geq 5$
and dimensions
![]() $2.999999\leq s\leq 3$
,
$2.999999\leq s\leq 3$
,
 $$ \begin{align}\left(\frac{1}{\sqrt{3}}-\frac{2}{m-\xi_m}\right)\frac{\mathcal{M}^s_\infty(E\cap Q_*)}{(\operatorname{\mathrm{side}}\nolimits Q_*)^s}\leq \left(\frac{2}{\sqrt{3}}m + 27\pi\frac{m^{-0.999999}}{1-m^{-1.999999}}\right)\omega^X_{Q\setminus E}(E\cap Q).\end{align} $$
$$ \begin{align}\left(\frac{1}{\sqrt{3}}-\frac{2}{m-\xi_m}\right)\frac{\mathcal{M}^s_\infty(E\cap Q_*)}{(\operatorname{\mathrm{side}}\nolimits Q_*)^s}\leq \left(\frac{2}{\sqrt{3}}m + 27\pi\frac{m^{-0.999999}}{1-m^{-1.999999}}\right)\omega^X_{Q\setminus E}(E\cap Q).\end{align} $$
Proof In (3.3), take
![]() $n=3$
and
$n=3$
and
![]() $k=1$
. Bound the factor
$k=1$
. Bound the factor
![]() $m^{2-s}/(1-m^{1-s})$
appearing in
$m^{2-s}/(1-m^{1-s})$
appearing in
![]() $O(3,m,s)$
using the assumption
$O(3,m,s)$
using the assumption
![]() $s\geq 2.999999$
.
$s\geq 2.999999$
.
Corollary 3.5 Suppose
![]() $n=4$
. For all integers
$n=4$
. For all integers
![]() $m\geq 7$
and dimensions
$m\geq 7$
and dimensions
![]() $3.999999\leq s\leq 4$
,
$3.999999\leq s\leq 4$
,
 $$ \begin{align}\left(\frac{1}{4}-\left(\frac{2}{m-\xi_m}\right)^2\right)\frac{\mathcal{M}^s_\infty(E\cap Q_*)}{(\operatorname{\mathrm{side}}\nolimits Q_*)^s}\leq\left(\frac{1}{4}m^2 + 32\pi^2 \frac{m^{0.000001}}{1-m^{-1.999999}}\right)\omega^X_{Q\setminus E}(E\cap Q).\end{align} $$
$$ \begin{align}\left(\frac{1}{4}-\left(\frac{2}{m-\xi_m}\right)^2\right)\frac{\mathcal{M}^s_\infty(E\cap Q_*)}{(\operatorname{\mathrm{side}}\nolimits Q_*)^s}\leq\left(\frac{1}{4}m^2 + 32\pi^2 \frac{m^{0.000001}}{1-m^{-1.999999}}\right)\omega^X_{Q\setminus E}(E\cap Q).\end{align} $$
Proof In (3.3), take
![]() $n=4$
and
$n=4$
and
![]() $k=1$
. Bound the factor
$k=1$
. Bound the factor
![]() $m^{4-s}/(1-m^{2-s})$
appearing in
$m^{4-s}/(1-m^{2-s})$
appearing in
![]() $O(4,m,s)$
using the assumption
$O(4,m,s)$
using the assumption
![]() $s\geq 3.999999$
.
$s\geq 3.999999$
.
A rectangle in
![]() $\mathbb {R}^{n}$
is a set of the form
$\mathbb {R}^{n}$
is a set of the form
![]() $[x_1,x_1+s_1]\times \cdots \times [x_n,x_n+s_n]$
with
$[x_1,x_1+s_1]\times \cdots \times [x_n,x_n+s_n]$
with
![]() $s_1,\dots ,s_n>0$
. Iterating the strong Markov property, one gets an estimate on harmonic measure of the portion of the boundary lying inside a sequence of nested rectangles: Brownian motion cannot reach the innermost rectangle without passing through the outer rectangles.
$s_1,\dots ,s_n>0$
. Iterating the strong Markov property, one gets an estimate on harmonic measure of the portion of the boundary lying inside a sequence of nested rectangles: Brownian motion cannot reach the innermost rectangle without passing through the outer rectangles.
Lemma 3.6 Let
![]() $n\geq 3$
, and let
$n\geq 3$
, and let
![]() $\Omega \subsetneq \mathbb {R}^{n}$
be a domain. Let
$\Omega \subsetneq \mathbb {R}^{n}$
be a domain. Let
![]() $H_1,\dots ,H_k$
be rectangles in
$H_1,\dots ,H_k$
be rectangles in
![]() $\mathbb {R}^{n}$
that are strictly nested in the sense that
$\mathbb {R}^{n}$
that are strictly nested in the sense that
![]() $H_k\subset \operatorname{\mathrm{int}}\nolimits {H_{k-1}}$
,
$H_k\subset \operatorname{\mathrm{int}}\nolimits {H_{k-1}}$
,
![]() $H_{k-1}\subset \operatorname{\mathrm{int}}\nolimits H_{k-2}$
, …,
$H_{k-1}\subset \operatorname{\mathrm{int}}\nolimits H_{k-2}$
, …,
![]() $H_2\subset \operatorname{\mathrm{int}}\nolimits {H_1}$
. Write
$H_2\subset \operatorname{\mathrm{int}}\nolimits {H_1}$
. Write
![]() $G^{\prime }_i=\Omega \cap \partial (\Omega \setminus H_i)\subset \partial H_i=G_i$
for each i. If
$G^{\prime }_i=\Omega \cap \partial (\Omega \setminus H_i)\subset \partial H_i=G_i$
for each i. If
![]() $X\in \Omega \setminus H_1$
, then
$X\in \Omega \setminus H_1$
, then
 $$ \begin{align}\omega^{X}_\Omega(H_k)\leq \omega^{X}_{\Omega\setminus H_1}(G^{\prime}_1)\left(\sup_{X_1\in G^{\prime}_1} \omega^{X_1}_{\Omega\setminus H_2}(G^{\prime}_2)\right) \cdots\left(\sup_{X_{k-1}\in G^{\prime}_{k-1}}\omega^{X_{k-1}}_{\Omega\setminus H_{k}}(G_k)\right).\end{align} $$
$$ \begin{align}\omega^{X}_\Omega(H_k)\leq \omega^{X}_{\Omega\setminus H_1}(G^{\prime}_1)\left(\sup_{X_1\in G^{\prime}_1} \omega^{X_1}_{\Omega\setminus H_2}(G^{\prime}_2)\right) \cdots\left(\sup_{X_{k-1}\in G^{\prime}_{k-1}}\omega^{X_{k-1}}_{\Omega\setminus H_{k}}(G_k)\right).\end{align} $$
(Except for the final instance,
![]() $G_k$
, all instances of a “G” in the formula are
$G_k$
, all instances of a “G” in the formula are
![]() $G^{\prime }_i$
.)
$G^{\prime }_i$
.)
Proof We induct on the number of rectangles. The base case
![]() $\omega ^X_\Omega (H_1)\leq \omega ^{X}_{\Omega \setminus H_1}(G_1)$
holds by the maximum principle. For the induction step, suppose that the lemma holds with k nested rectangles for some
$\omega ^X_\Omega (H_1)\leq \omega ^{X}_{\Omega \setminus H_1}(G_1)$
holds by the maximum principle. For the induction step, suppose that the lemma holds with k nested rectangles for some
![]() $k\geq 1$
. Let
$k\geq 1$
. Let
![]() $H_1,\ldots , H_{k+1}$
be rectangles with
$H_1,\ldots , H_{k+1}$
be rectangles with
![]() $H_{j+1}\subset \operatorname{\mathrm{int}}\nolimits {H_{j}}$
for all
$H_{j+1}\subset \operatorname{\mathrm{int}}\nolimits {H_{j}}$
for all
![]() $1\leq j\leq k$
and fix
$1\leq j\leq k$
and fix
![]() $X\in \Omega \setminus H_1$
. Note that every
$X\in \Omega \setminus H_1$
. Note that every
![]() $X_1\in G^{\prime }_1$
lies outside of
$X_1\in G^{\prime }_1$
lies outside of
![]() $H_2$
. Thus, the inductive hypothesis applied with
$H_2$
. Thus, the inductive hypothesis applied with
![]() $H_2,\dots , H_{k+1}$
guarantees that
$H_2,\dots , H_{k+1}$
guarantees that
 $$ \begin{align*}\omega^{X_1}_\Omega(H_{k+1})\leq \omega^{X_1}_{\Omega\setminus H_2}(G^{\prime}_2)\left(\sup_{X_2\in G^{\prime}_2} \omega^{X_2}_{\Omega\setminus H_3}(G^{\prime}_3)\right) \cdots\left(\sup_{X_{k}\in G^{\prime}_{k}}\omega^{X_{k}}_{\Omega\setminus H_{k+1}}(G_{k+1})\right).\end{align*} $$
$$ \begin{align*}\omega^{X_1}_\Omega(H_{k+1})\leq \omega^{X_1}_{\Omega\setminus H_2}(G^{\prime}_2)\left(\sup_{X_2\in G^{\prime}_2} \omega^{X_2}_{\Omega\setminus H_3}(G^{\prime}_3)\right) \cdots\left(\sup_{X_{k}\in G^{\prime}_{k}}\omega^{X_{k}}_{\Omega\setminus H_{k+1}}(G_{k+1})\right).\end{align*} $$
(When
![]() $k=1$
, this formula should be read as
$k=1$
, this formula should be read as
![]() $\omega ^{X_1}_\Omega (H_2)\leq \omega ^{X_1}_{\Omega \setminus H_2}(G_2)$
.) Since
$\omega ^{X_1}_\Omega (H_2)\leq \omega ^{X_1}_{\Omega \setminus H_2}(G_2)$
.) Since
![]() $\Omega \setminus H_1\subset \Omega $
, the strong Markov property (see, e.g., [Reference Doob12, p. 117]) ensures that
$\Omega \setminus H_1\subset \Omega $
, the strong Markov property (see, e.g., [Reference Doob12, p. 117]) ensures that
 $$ \begin{align*} \omega^{X}_\Omega(H_{k+1}) &= \omega^{X}_{\Omega\setminus H_1}(H_{k+1}\cap\partial\Omega) + \int_{\Omega\cap \partial(\Omega\setminus H_1)} \omega^{X_1}_{\Omega}(H_{k+1})\,d\omega^{X}_{\Omega\setminus H_1}(X_1)\\ &= \int_{G^{\prime}_1} \omega^{X_1}_{\Omega}(H_{k+1})\,d\omega^{X}_{\Omega\setminus H_1}(X_1) \leq \omega^{X}_{\Omega\setminus H_1}(G^{\prime}_1)\sup_{X_1\in G^{\prime}_1} \omega^{X_1}_{\Omega}(H_{k+1}),\end{align*} $$
$$ \begin{align*} \omega^{X}_\Omega(H_{k+1}) &= \omega^{X}_{\Omega\setminus H_1}(H_{k+1}\cap\partial\Omega) + \int_{\Omega\cap \partial(\Omega\setminus H_1)} \omega^{X_1}_{\Omega}(H_{k+1})\,d\omega^{X}_{\Omega\setminus H_1}(X_1)\\ &= \int_{G^{\prime}_1} \omega^{X_1}_{\Omega}(H_{k+1})\,d\omega^{X}_{\Omega\setminus H_1}(X_1) \leq \omega^{X}_{\Omega\setminus H_1}(G^{\prime}_1)\sup_{X_1\in G^{\prime}_1} \omega^{X_1}_{\Omega}(H_{k+1}),\end{align*} $$
where
![]() $\omega ^{X}_{\Omega \setminus H_1}(H_{k+1}\cap \partial \Omega )=0$
trivially, since
$\omega ^{X}_{\Omega \setminus H_1}(H_{k+1}\cap \partial \Omega )=0$
trivially, since
![]() $H_{k+1}$
is contained in the exterior of
$H_{k+1}$
is contained in the exterior of
![]() $\Omega \setminus H_1$
. Combining the two displayed equations gives the desired inequality for
$\Omega \setminus H_1$
. Combining the two displayed equations gives the desired inequality for
![]() $H_1,\dots ,H_{k+1}$
.
$H_1,\dots ,H_{k+1}$
.
A nearly identical argument gives the following dual inequality.
Lemma 3.7 Let
![]() $n\geq 3$
, and let
$n\geq 3$
, and let
![]() $\Omega \subsetneq \mathbb {R}^{n}$
be a domain. Let
$\Omega \subsetneq \mathbb {R}^{n}$
be a domain. Let
![]() $H_1, H_2$
be rectangles in
$H_1, H_2$
be rectangles in
![]() $\mathbb {R}^{n}$
with
$\mathbb {R}^{n}$
with
![]() $H_2\subset \operatorname{\mathrm{int}}\nolimits {H_1}$
. Write
$H_2\subset \operatorname{\mathrm{int}}\nolimits {H_1}$
. Write
![]() $G^{\prime }_i=\Omega \cap \partial (\Omega \setminus H_i)\subset \partial H_i=G_i$
for all i. If
$G^{\prime }_i=\Omega \cap \partial (\Omega \setminus H_i)\subset \partial H_i=G_i$
for all i. If
![]() $X\in \Omega \setminus H_1$
, then
$X\in \Omega \setminus H_1$
, then
 $$ \begin{align}\omega^{X}_\Omega(H_2)\geq \omega^X_{\Omega\setminus H_1}(G^{\prime}_1)\left(\inf_{X_1\in G^{\prime}_1} \omega^{X_1}_{\Omega\setminus H_2}(G_2)\right).\end{align} $$
$$ \begin{align}\omega^{X}_\Omega(H_2)\geq \omega^X_{\Omega\setminus H_1}(G^{\prime}_1)\left(\inf_{X_1\in G^{\prime}_1} \omega^{X_1}_{\Omega\setminus H_2}(G_2)\right).\end{align} $$
4 Bounding Bourgain’s constant from below
Recall that Bourgain’s constant
![]() $b_n$
is the largest value such that the upper Hausdorff dimension of harmonic measure is at most
$b_n$
is the largest value such that the upper Hausdorff dimension of harmonic measure is at most
![]() $n-b_n$
for all domains
$n-b_n$
for all domains
![]() $\Omega \subset \mathbb {R}^n$
. The following theorem is based on the demonstration in [Reference Bourgain10] that
$\Omega \subset \mathbb {R}^n$
. The following theorem is based on the demonstration in [Reference Bourgain10] that
![]() $b_3>0$
and implements ideas from [Reference Badger and Genschaw4]. It reduces the problem of bounding
$b_3>0$
and implements ideas from [Reference Badger and Genschaw4]. It reduces the problem of bounding
![]() $b_n$
from below to estimation of constants appearing in Bourgain’s estimate and selection of parameters m,
$b_n$
from below to estimation of constants appearing in Bourgain’s estimate and selection of parameters m,
![]() $\eta $
, h, and d satisfying the constraint (4.2). By working exclusively with m-adic cubes and net contents – without passing through Hausdorff contents – we avoid introducing an unnecessary source of error as was done in the original argument. This is important in the context of Theorem 1.2.
$\eta $
, h, and d satisfying the constraint (4.2). By working exclusively with m-adic cubes and net contents – without passing through Hausdorff contents – we avoid introducing an unnecessary source of error as was done in the original argument. This is important in the context of Theorem 1.2.
Theorem 4.1 Let
![]() $n\geq 3$
, and let
$n\geq 3$
, and let
![]() $m\geq 5$
. Suppose that
$m\geq 5$
. Suppose that
![]() $\epsilon>0$
and
$\epsilon>0$
and
![]() $\alpha>0$
are constants such that Bourgain’s estimate holds in the sense that for all
$\alpha>0$
are constants such that Bourgain’s estimate holds in the sense that for all
![]() $Q_*$
and Q, as in Lemma 3.1, for all closed sets
$Q_*$
and Q, as in Lemma 3.1, for all closed sets
![]() $E\subset \mathbb {R}^n$
, for all
$E\subset \mathbb {R}^n$
, for all
![]() $X\in Q_*\setminus E$
, and for all
$X\in Q_*\setminus E$
, and for all
![]() $n-\epsilon <s\leq n$
, we have
$n-\epsilon <s\leq n$
, we have
Let
![]() $\eta>0$
be any number such that
$\eta>0$
be any number such that
![]() $(2-m^{-n})\alpha \eta \leq 1-m^{-n}$
. Finally, suppose that
$(2-m^{-n})\alpha \eta \leq 1-m^{-n}$
. Finally, suppose that
![]() $1\leq h<m/2$
and
$1\leq h<m/2$
and
![]() $d\geq 1$
are integers such that
$d\geq 1$
are integers such that
Then
![]() $b_n\geq \lambda \rho /(\lambda +\rho )$
, where
$b_n\geq \lambda \rho /(\lambda +\rho )$
, where
In order to prove the theorem, we start with an auxiliary estimate.
Lemma 4.2 If
![]() $n\geq 3$
,
$n\geq 3$
,
![]() $m\geq 5$
, and
$m\geq 5$
, and
![]() $d\geq 1$
are integers and
$d\geq 1$
are integers and
![]() $(2-m^{-n})a\leq 1-m^{-n}$
, then
$(2-m^{-n})a\leq 1-m^{-n}$
, then
holds for all values of
![]() $\rho $
in the range
$\rho $
in the range
Remark. As a referee noted, the proof below shows that by imposing stricter constraints on m and d, the constant
![]() $0.914186$
can be made arbitrarily close to
$0.914186$
can be made arbitrarily close to
![]() $\sqrt {2}-1/2=0.914213\ldots $
. We shall not dwell on this point, because it would not change the first significant digit of our estimate on
$\sqrt {2}-1/2=0.914213\ldots $
. We shall not dwell on this point, because it would not change the first significant digit of our estimate on
![]() $b_3$
and
$b_3$
and
![]() $b_4$
in Theorem 1.2. It may be worth exploring how much the bound can be improved without using the relaxation
$b_4$
in Theorem 1.2. It may be worth exploring how much the bound can be improved without using the relaxation
![]() $c-x<1\Rightarrow c - c^{d+2}x<1$
, but this is beyond the scope of the current paper.
$c-x<1\Rightarrow c - c^{d+2}x<1$
, but this is beyond the scope of the current paper.
Proof Rewriting (4.4) using the formula for partial geometric series, we want to find the largest possible
![]() $\rho \geq 0$
such that
$\rho \geq 0$
such that
Rearranging, expanding the products, and cancelling like terms, our goal becomes
Set
![]() $\rho =\log _m(c)$
with
$\rho =\log _m(c)$
with
![]() $c\geq 1$
, close to
$c\geq 1$
, close to
![]() $1$
, to be found below. Then we would like
$1$
, to be found below. Then we would like
 $$ \begin{align*}c-c^{d+2}\underbrace{m^{-(d+1)n}(1-(1-a)m^{-n}-a/c)}_x<1.\end{align*} $$
$$ \begin{align*}c-c^{d+2}\underbrace{m^{-(d+1)n}(1-(1-a)m^{-n}-a/c)}_x<1.\end{align*} $$
Since
![]() $c\geq 1$
and
$c\geq 1$
and
![]() $x>0$
, the inequality
$x>0$
, the inequality
![]() $c-c^{d+2}x<1$
is implied by
$c-c^{d+2}x<1$
is implied by
![]() $c-x<1$
. Hence, it suffices to find
$c-x<1$
. Hence, it suffices to find
![]() $c\geq 1$
such that
$c\geq 1$
such that
![]() $c-m^{-(d+1)n}(1-(1-a)m^{-n}-a/c)< 1$
. Equivalently,
$c-m^{-(d+1)n}(1-(1-a)m^{-n}-a/c)< 1$
. Equivalently,
 $$ \begin{align*}c^2-(1+\underbrace{m^{-(d+1)n}(1-(1-a)m^{-n})}_{y})\,c+\underbrace{am^{-(d+1)n}}_z< 0.\end{align*} $$
$$ \begin{align*}c^2-(1+\underbrace{m^{-(d+1)n}(1-(1-a)m^{-n})}_{y})\,c+\underbrace{am^{-(d+1)n}}_z< 0.\end{align*} $$
Now,
![]() $c^2-(1+y)c+z< 0$
holds at
$c^2-(1+y)c+z< 0$
holds at
![]() $c=1$
provided that
$c=1$
provided that
![]() $z<y$
. In our case, we need
$z<y$
. In our case, we need
![]() $(1-a)m^{-n}< 1-a$
, which is true since
$(1-a)m^{-n}< 1-a$
, which is true since
![]() $a<1$
. It follows that we may select c to be any number between 1 and the greater of the two roots of
$a<1$
. It follows that we may select c to be any number between 1 and the greater of the two roots of
![]() $c^2-(1+y)c+z=0$
. That is,
$c^2-(1+y)c+z=0$
. That is,
 $$ \begin{align*}1\leq c < \frac{1+y+\sqrt{(1+y)^2-4z}}{2}.\end{align*} $$
$$ \begin{align*}1\leq c < \frac{1+y+\sqrt{(1+y)^2-4z}}{2}.\end{align*} $$
Well,
![]() $1+(\sqrt {2}-1)(2y-4z)\leq \sqrt {1+2y-4z}<\sqrt {(1+y)^2-4z}$
provided that
$1+(\sqrt {2}-1)(2y-4z)\leq \sqrt {1+2y-4z}<\sqrt {(1+y)^2-4z}$
provided that
![]() $0\leq 2y-4z<1$
. (To verify the first inequality, start by squaring both sides.) In particular,
$0\leq 2y-4z<1$
. (To verify the first inequality, start by squaring both sides.) In particular,
![]() $4z\leq 2y$
as long as
$4z\leq 2y$
as long as
![]() $4a \leq 2-2(1-a)m^{-n}$
; this holds by our demand that
$4a \leq 2-2(1-a)m^{-n}$
; this holds by our demand that
![]() $(2-m^{-n})a\leq 1-m^{-n}$
. Hence, we can choose
$(2-m^{-n})a\leq 1-m^{-n}$
. Hence, we can choose
 $$ \begin{align*} 1\leq c&\leq \frac{1+y+1+(\sqrt{2}-1)(2y-4z)}{2}\\ &=1+\underbrace{(\sqrt{2}-1/2)m^{-(d+1)n}\left(\frac{(1-2(\sqrt{2}-1))a}{(\sqrt{2}-1/2)-(1-a)m^{-n}}\right)}_w. \end{align*} $$
$$ \begin{align*} 1\leq c&\leq \frac{1+y+1+(\sqrt{2}-1)(2y-4z)}{2}\\ &=1+\underbrace{(\sqrt{2}-1/2)m^{-(d+1)n}\left(\frac{(1-2(\sqrt{2}-1))a}{(\sqrt{2}-1/2)-(1-a)m^{-n}}\right)}_w. \end{align*} $$
Thus, (4.4) holds if
![]() $0\leq \rho \leq \ln (1+w)/\ln (m)$
. Estimating
$0\leq \rho \leq \ln (1+w)/\ln (m)$
. Estimating
and
![]() $1-2(\sqrt {2}-1)a/(\sqrt {2}-1/2)-(1-a)m^{-n} \geq (1-a)(1-m^{-n})$
and checking that
$1-2(\sqrt {2}-1)a/(\sqrt {2}-1/2)-(1-a)m^{-n} \geq (1-a)(1-m^{-n})$
and checking that
![]() $(\sqrt {2}-1/2)\cdot 0.99997=0.914186\ldots $
, we conclude that (4.5) implies (4.4).
$(\sqrt {2}-1/2)\cdot 0.99997=0.914186\ldots $
, we conclude that (4.5) implies (4.4).
Proof of Theorem 4.1
Let n, m,
![]() $\epsilon $
,
$\epsilon $
,
![]() $\alpha $
,
$\alpha $
,
![]() $\eta $
, h, d,
$\eta $
, h, d,
![]() $\gamma $
,
$\gamma $
,
![]() $\lambda $
, and
$\lambda $
, and
![]() $\rho $
be given according to the statement of the theorem. Shrinking
$\rho $
be given according to the statement of the theorem. Shrinking
![]() $\rho $
as needed, we may assume without loss of generality that
$\rho $
as needed, we may assume without loss of generality that
![]() $\rho <\epsilon $
. Let
$\rho <\epsilon $
. Let
![]() $\Delta =\Delta ^m(\mathbb {R}^n)$
, let
$\Delta =\Delta ^m(\mathbb {R}^n)$
, let
![]() $\Omega \subsetneq \mathbb {R}^n$
be a domain, let
$\Omega \subsetneq \mathbb {R}^n$
be a domain, let
![]() $\Omega ^c=\mathbb {R}^n\setminus \Omega $
, let
$\Omega ^c=\mathbb {R}^n\setminus \Omega $
, let
![]() $X\in \Omega $
, and let
$X\in \Omega $
, and let
![]() $\omega =\omega ^{X}_{\Omega }$
. Define
$\omega =\omega ^{X}_{\Omega }$
. Define
![]() $\vec \Delta $
as in (3.1). We say
$\vec \Delta $
as in (3.1). We say
![]() $(Q,Q_*)$
is an admissible pair if
$(Q,Q_*)$
is an admissible pair if
![]() $Q\in \vec \Delta $
,
$Q\in \vec \Delta $
,
![]() $Q_*\in \Delta $
,
$Q_*\in \Delta $
,
![]() $\operatorname{\mathrm{side}}\nolimits Q_*=m^{-1}\operatorname{\mathrm{side}}\nolimits Q$
, and
$\operatorname{\mathrm{side}}\nolimits Q_*=m^{-1}\operatorname{\mathrm{side}}\nolimits Q$
, and
![]() $\overline {Q_*}$
includes the center of Q. For every admissible pair
$\overline {Q_*}$
includes the center of Q. For every admissible pair
![]() $(Q,Q_*)$
, the Bourgain type estimate (4.1) with
$(Q,Q_*)$
, the Bourgain type estimate (4.1) with
![]() $s=n-\rho $
implies either
$s=n-\rho $
implies either
or
To bound
![]() $\overline {\dim }_H\,\omega $
from above by
$\overline {\dim }_H\,\omega $
from above by
![]() $n-\lambda \rho /(\lambda +\rho )$
, we aim to use Lemma 2.2. Because scaling and translating the domain in space and changing the pole has no effect on the Hausdorff dimension of harmonic measure, we may assume without loss of generality that if
$n-\lambda \rho /(\lambda +\rho )$
, we aim to use Lemma 2.2. Because scaling and translating the domain in space and changing the pole has no effect on the Hausdorff dimension of harmonic measure, we may assume without loss of generality that if
![]() $P\in \Delta $
,
$P\in \Delta $
,
![]() $\operatorname{\mathrm{side}}\nolimits P\leq 1$
, and
$\operatorname{\mathrm{side}}\nolimits P\leq 1$
, and
![]() $X\in \overline {P}$
, then
$X\in \overline {P}$
, then
![]() $\overline {P}$
is disjoint from
$\overline {P}$
is disjoint from
![]() $\partial \Omega $
. For any such cube P,
$\partial \Omega $
. For any such cube P,
trivially.
To continue, suppose that
![]() $P\in \Delta $
is an m-adic cube with
$P\in \Delta $
is an m-adic cube with
![]() $\operatorname{\mathrm{side}}\nolimits P\leq 1$
, for which
$\operatorname{\mathrm{side}}\nolimits P\leq 1$
, for which
![]() $X\not \in \overline {P}$
. For any
$X\not \in \overline {P}$
. For any
![]() $j\geq 1$
, let
$j\geq 1$
, let
![]() $\operatorname{\mathsf{Child}}\nolimits ^j(P)$
denote the set of all jth generation descendents of P in the tree
$\operatorname{\mathsf{Child}}\nolimits ^j(P)$
denote the set of all jth generation descendents of P in the tree
![]() $\Delta $
. For example,
$\Delta $
. For example,
![]() $\operatorname{\mathsf{Child}}\nolimits ^2(P)=\{R\in \Delta :R\subset P,\, \operatorname{\mathrm{side}}\nolimits R = m^{-2}\operatorname{\mathrm{side}}\nolimits P\}$
is the set of all grandchildren of P. Keeping in mind our goal of checking the hypothesis of Lemma 2.2, we consider two alternatives. Under Alternative 1, we will show that P satisfies (2.1). Under Alternative 2, we will show that P satisfies (2.2).
$\operatorname{\mathsf{Child}}\nolimits ^2(P)=\{R\in \Delta :R\subset P,\, \operatorname{\mathrm{side}}\nolimits R = m^{-2}\operatorname{\mathrm{side}}\nolimits P\}$
is the set of all grandchildren of P. Keeping in mind our goal of checking the hypothesis of Lemma 2.2, we consider two alternatives. Under Alternative 1, we will show that P satisfies (2.1). Under Alternative 2, we will show that P satisfies (2.2).
Alternative 1. Suppose that the estimate (4.7) holds for some admissible pair
![]() $(Q,Q_*)$
with
$(Q,Q_*)$
with
![]() $Q_*\in \operatorname{\mathsf{Child}}\nolimits ^{d+1}(P)$
. Let
$Q_*\in \operatorname{\mathsf{Child}}\nolimits ^{d+1}(P)$
. Let
![]() $Q_*^{\uparrow j}\in \Delta $
denote the jth ancestor of
$Q_*^{\uparrow j}\in \Delta $
denote the jth ancestor of
![]() $Q_*$
in
$Q_*$
in
![]() $\Delta $
. Covering
$\Delta $
. Covering
![]() $\Omega ^c\cap P$
by
$\Omega ^c\cap P$
by
![]() $\operatorname{\mathsf{Child}}\nolimits (P)\setminus \{Q_*^{\uparrow d}\}$
,
$\operatorname{\mathsf{Child}}\nolimits (P)\setminus \{Q_*^{\uparrow d}\}$
,
![]() $\operatorname{\mathsf{Child}}\nolimits (Q_*^{\uparrow d})\setminus \{Q_*^{\uparrow d-1}\}$
, …,
$\operatorname{\mathsf{Child}}\nolimits (Q_*^{\uparrow d})\setminus \{Q_*^{\uparrow d-1}\}$
, …,
![]() $\operatorname{\mathsf{Child}}\nolimits (Q_*^{\uparrow 1})\setminus \{Q_*\}$
, and
$\operatorname{\mathsf{Child}}\nolimits (Q_*^{\uparrow 1})\setminus \{Q_*\}$
, and
![]() $\Omega ^c\cap Q_*$
, we obtain (Figure 3)
$\Omega ^c\cap Q_*$
, we obtain (Figure 3)
 $$ \begin{align*} \mathcal{M}^{n-\rho}_{m^{-1}\operatorname{\mathrm{side}}\nolimits P}(\Omega^c\cap P)&< (m^{n}-1)\left((\operatorname{\mathrm{side}}\nolimits Q_*^{\uparrow d})^{n-\rho}+\cdots+(\operatorname{\mathrm{side}}\nolimits Q_*)^{n-\rho}\right)\\ &\quad +\alpha\eta(\operatorname{\mathrm{side}}\nolimits Q_*)^{n-\rho}. \end{align*} $$
$$ \begin{align*} \mathcal{M}^{n-\rho}_{m^{-1}\operatorname{\mathrm{side}}\nolimits P}(\Omega^c\cap P)&< (m^{n}-1)\left((\operatorname{\mathrm{side}}\nolimits Q_*^{\uparrow d})^{n-\rho}+\cdots+(\operatorname{\mathrm{side}}\nolimits Q_*)^{n-\rho}\right)\\ &\quad +\alpha\eta(\operatorname{\mathrm{side}}\nolimits Q_*)^{n-\rho}. \end{align*} $$
Rewriting each side length in terms of
![]() $\operatorname{\mathrm{side}}\nolimits P$
and rearranging,
$\operatorname{\mathrm{side}}\nolimits P$
and rearranging,
 $$ \begin{align*}\frac{\mathcal{M}^{n-\rho}_{m^{-1}\operatorname{\mathrm{side}}\nolimits P}(\Omega^c\cap P)}{(\operatorname{\mathrm{side}}\nolimits P)^{n-\rho}} \leq (m^{n}-1)(m^{-(n-\rho)}+\cdots+m^{-(d+1)(n-\rho)})+\alpha\eta m^{-(d+1)(n-\rho)}.\end{align*} $$
$$ \begin{align*}\frac{\mathcal{M}^{n-\rho}_{m^{-1}\operatorname{\mathrm{side}}\nolimits P}(\Omega^c\cap P)}{(\operatorname{\mathrm{side}}\nolimits P)^{n-\rho}} \leq (m^{n}-1)(m^{-(n-\rho)}+\cdots+m^{-(d+1)(n-\rho)})+\alpha\eta m^{-(d+1)(n-\rho)}.\end{align*} $$
Applying Lemma 4.2 with
![]() $a=\alpha \eta $
, we conclude that
$a=\alpha \eta $
, we conclude that

Figure 3: Optimal covering of
![]() $\Omega ^c\cap P$
under the assumption that the net content of
$\Omega ^c\cap P$
under the assumption that the net content of
![]() $\Omega ^c$
inside of some
$\Omega ^c$
inside of some
![]() $(d+1)$
-descendent
$(d+1)$
-descendent
![]() $Q_*$
is small.
$Q_*$
is small.
Alternative 2. Suppose that the estimate (4.6) holds for every admissible pair
![]() $(Q,Q_*)$
with
$(Q,Q_*)$
with
![]() $Q_*\in \operatorname{\mathsf{Child}}\nolimits ^{d+1}(P)$
. Partition P into annular rings of dth generation descendents. Working from the outside to the inside, define
$Q_*\in \operatorname{\mathsf{Child}}\nolimits ^{d+1}(P)$
. Partition P into annular rings of dth generation descendents. Working from the outside to the inside, define
![]() $A_0=\emptyset $
,
$A_0=\emptyset $
,
![]() $P_0= P$
,
$P_0= P$
,
 $$ \begin{align*} A_1 &= \bigcup\{Q\in\operatorname{\mathsf{Child}}\nolimits^d(P):Q\not\subset A_0,\, \overline{Q}\cap \partial P_0\neq\emptyset\}, & P_1&=P_0\setminus A_1,\\ A_2 &= \bigcup\{Q\in\operatorname{\mathsf{Child}}\nolimits^d(P):Q\not\subset A_1,\, \overline{Q}\cap \partial P_1\neq\emptyset\}, & P_2&=P_1\setminus A_2,\\ &\ \,\vdots &&\ \,\vdots\\ A_{M} &= \bigcup\{Q\in\operatorname{\mathsf{Child}}\nolimits^d(P):Q\not\subset A_{M-1},\, \overline{Q}\cap \partial P_{M-1}\neq\emptyset\}, && \!\!\!\!\!\!\!\!\!\!P_{M}=P_{M-1}\setminus A_M,\\ A_{M+1}&= \bigcup\{Q\in\operatorname{\mathsf{Child}}\nolimits^d(P):Q\not\subset A_{M},\, \overline{Q}\cap \partial P_M \neq \emptyset\}=P_M, && \!\!\!\!\!\!\!\!\!\!P_{M+1}=\emptyset, \end{align*} $$
$$ \begin{align*} A_1 &= \bigcup\{Q\in\operatorname{\mathsf{Child}}\nolimits^d(P):Q\not\subset A_0,\, \overline{Q}\cap \partial P_0\neq\emptyset\}, & P_1&=P_0\setminus A_1,\\ A_2 &= \bigcup\{Q\in\operatorname{\mathsf{Child}}\nolimits^d(P):Q\not\subset A_1,\, \overline{Q}\cap \partial P_1\neq\emptyset\}, & P_2&=P_1\setminus A_2,\\ &\ \,\vdots &&\ \,\vdots\\ A_{M} &= \bigcup\{Q\in\operatorname{\mathsf{Child}}\nolimits^d(P):Q\not\subset A_{M-1},\, \overline{Q}\cap \partial P_{M-1}\neq\emptyset\}, && \!\!\!\!\!\!\!\!\!\!P_{M}=P_{M-1}\setminus A_M,\\ A_{M+1}&= \bigcup\{Q\in\operatorname{\mathsf{Child}}\nolimits^d(P):Q\not\subset A_{M},\, \overline{Q}\cap \partial P_M \neq \emptyset\}=P_M, && \!\!\!\!\!\!\!\!\!\!P_{M+1}=\emptyset, \end{align*} $$
where
![]() $m^d=2M+1$
, if m is odd, and
$m^d=2M+1$
, if m is odd, and
![]() $m^d=2M+2$
, if m is even. Next, for each annulus
$m^d=2M+2$
, if m is even. Next, for each annulus
![]() $A_i$
, with
$A_i$
, with
![]() $1\leq i\leq M$
, choose a rectangle
$1\leq i\leq M$
, choose a rectangle
![]() $H_i$
such that (i)
$H_i$
such that (i)
![]() $G_i:=\partial H_i \subset A_i$
separates
$G_i:=\partial H_i \subset A_i$
separates
![]() $\partial P_{i-1}$
from
$\partial P_{i-1}$
from
![]() $\partial P_i$
and (ii) for any
$\partial P_i$
and (ii) for any
![]() $Z\in G_i$
, there exists an admissible pair
$Z\in G_i$
, there exists an admissible pair
![]() $(Q,Q_*)$
with
$(Q,Q_*)$
with
![]() $Q_*\in \operatorname{\mathsf{Child}}\nolimits ^{d+1}(P)$
,
$Q_*\in \operatorname{\mathsf{Child}}\nolimits ^{d+1}(P)$
,
![]() $Z\in Q_*$
,
$Z\in Q_*$
,
![]() $Q\subset A_i$
, and
$Q\subset A_i$
, and
![]() $Q\cap A_{i+1}=\emptyset $
. There are a continuum of possibilities for each
$Q\cap A_{i+1}=\emptyset $
. There are a continuum of possibilities for each
![]() $H_i$
. Further, as in Lemma 3.6, assign
$H_i$
. Further, as in Lemma 3.6, assign
![]() $G_i':=\Omega \cap \partial (\Omega \setminus H_i)\subset G_i$
for each i. See Figure 4.
$G_i':=\Omega \cap \partial (\Omega \setminus H_i)\subset G_i$
for each i. See Figure 4.

Figure 4: A decomposition
![]() $P=\widetilde A_1\cup \dots \cup \widetilde A_h \cup P_{hm^{d-1}}$
when
$P=\widetilde A_1\cup \dots \cup \widetilde A_h \cup P_{hm^{d-1}}$
when
![]() $n=2$
,
$n=2$
,
![]() $m=9$
,
$m=9$
,
![]() $h=2$
, and
$h=2$
, and
![]() $d=1$
, where each little square represents a
$d=1$
, where each little square represents a
![]() $d+1$
descendent of P. Brownian motion, started outside of P, cannot reach the inner region
$d+1$
descendent of P. Brownian motion, started outside of P, cannot reach the inner region
![]() $P_{hm^{d-1}}$
without passing through surfaces
$P_{hm^{d-1}}$
without passing through surfaces
![]() $G_i$
(not displayed) drawn in the collars of white squares. Increasing h raises the number of annuli
$G_i$
(not displayed) drawn in the collars of white squares. Increasing h raises the number of annuli
![]() $\widetilde A_j$
of children of P. Increasing d yields a higher density
$\widetilde A_j$
of children of P. Increasing d yields a higher density
![]() $m^{d-1}$
of separating surfaces per annulus.
$m^{d-1}$
of separating surfaces per annulus.
Fix any
![]() $1\leq k\leq M$
. Later, we will choose
$1\leq k\leq M$
. Later, we will choose
![]() $k=k(m,h,d)$
. Let
$k=k(m,h,d)$
. Let
![]() $H_1,\dots , H_k$
and
$H_1,\dots , H_k$
and
![]() $G_1,\dots , G_k$
and
$G_1,\dots , G_k$
and
![]() $G^{\prime }_1,\dots ,G^{\prime }_k$
be given as above. In addition, by a slight abuse of notation, write
$G^{\prime }_1,\dots ,G^{\prime }_k$
be given as above. In addition, by a slight abuse of notation, write
![]() $H_{k+1}=\overline {P_k}$
and
$H_{k+1}=\overline {P_k}$
and
![]() $G_{k+1}=\partial P_k$
. Then
$G_{k+1}=\partial P_k$
. Then
![]() $H_{i+1}\subset \operatorname{\mathrm{int}}\nolimits {H_i}$
for all
$H_{i+1}\subset \operatorname{\mathrm{int}}\nolimits {H_i}$
for all
![]() $1\leq i\leq k$
. Recall that
$1\leq i\leq k$
. Recall that
![]() $X\not \in \overline {P}$
. On the one hand, by Lemma 3.6, the trivial observation
$X\not \in \overline {P}$
. On the one hand, by Lemma 3.6, the trivial observation
![]() $\omega ^{X_i}_{\Omega \setminus H_{i+1}}(G^{\prime }_{i+1})\leq \omega ^{X_i}_{\Omega \setminus H_{i+1}}(G_{i+1})$
, and the fact that we are in Alternative 2,
$\omega ^{X_i}_{\Omega \setminus H_{i+1}}(G^{\prime }_{i+1})\leq \omega ^{X_i}_{\Omega \setminus H_{i+1}}(G_{i+1})$
, and the fact that we are in Alternative 2,
 $$ \begin{align} \omega(P_k)&\leq \omega^{X}_{\Omega\setminus H_1}(G^{\prime}_1)\prod_{i=1}^k\sup_{X_{i}\in G^{\prime}_{i}\cap\Omega}\omega^{X_{i}}_{\Omega\setminus H_{i+1}}(G_{i+1}) \\ &\leq \omega^{X}_{\Omega\setminus H_1}(G^{\prime}_1)\prod_{i=1}^k\left(1-\inf_{X_i\in G^{\prime}_i\cap\Omega} \omega^{X_i}_{\Omega\setminus H_{i+1}}(A_i)\right) \leq \omega^{X}_{\Omega\setminus H_1}(G^{\prime}_1)(1-\eta)^k.\nonumber \end{align} $$
$$ \begin{align} \omega(P_k)&\leq \omega^{X}_{\Omega\setminus H_1}(G^{\prime}_1)\prod_{i=1}^k\sup_{X_{i}\in G^{\prime}_{i}\cap\Omega}\omega^{X_{i}}_{\Omega\setminus H_{i+1}}(G_{i+1}) \\ &\leq \omega^{X}_{\Omega\setminus H_1}(G^{\prime}_1)\prod_{i=1}^k\left(1-\inf_{X_i\in G^{\prime}_i\cap\Omega} \omega^{X_i}_{\Omega\setminus H_{i+1}}(A_i)\right) \leq \omega^{X}_{\Omega\setminus H_1}(G^{\prime}_1)(1-\eta)^k.\nonumber \end{align} $$
To verify the final inequality, fix
![]() $Z\in G^{\prime }_i$
and let
$Z\in G^{\prime }_i$
and let
![]() $(Q,Q_*)$
be the admissible pair given by property (ii) in the definition of
$(Q,Q_*)$
be the admissible pair given by property (ii) in the definition of
![]() $G_i$
. Then
$G_i$
. Then
![]() $\omega ^{Z}_{\Omega \setminus H_{i+1}}(A_i)\geq \omega ^{Z}_{\operatorname{\mathrm{int}}\nolimits {Q}\setminus \Omega ^c}(\Omega ^c\cap \operatorname{\mathrm{int}}\nolimits {Q}) \geq \eta $
by the maximum principle and (4.6). On the other hand,
$\omega ^{Z}_{\Omega \setminus H_{i+1}}(A_i)\geq \omega ^{Z}_{\operatorname{\mathrm{int}}\nolimits {Q}\setminus \Omega ^c}(\Omega ^c\cap \operatorname{\mathrm{int}}\nolimits {Q}) \geq \eta $
by the maximum principle and (4.6). On the other hand,
by Lemma 3.7, the maximum principle, and (4.6). Combining (4.10) and (4.11), we obtain
The consequence of this estimate is that if k (hence M, hence d) is sufficiently large, then
![]() $\omega (P_k)$
is arbitrarily small relative to
$\omega (P_k)$
is arbitrarily small relative to
![]() $\omega (P)$
.
$\omega (P)$
.
To proceed, note that each union
![]() $\widetilde A_j=A_{1+(j-1)m^{d-1}}\cup \dots \cup A_{m^{d-1}+(j-1)m^{d-1}}$
of
$\widetilde A_j=A_{1+(j-1)m^{d-1}}\cup \dots \cup A_{m^{d-1}+(j-1)m^{d-1}}$
of
![]() $m^{d-1}$
consecutive rings
$m^{d-1}$
consecutive rings
![]() $A_i$
of d-descendents is an annulus formed from children of P. That is,
$A_i$
of d-descendents is an annulus formed from children of P. That is,
![]() $\widetilde A_1$
is the outermost annulus of children,
$\widetilde A_1$
is the outermost annulus of children,
![]() $\widetilde A_2$
is the second annulus of children, and so on. Assign
$\widetilde A_2$
is the second annulus of children, and so on. Assign
![]() $k=hm^{d-1}$
, with h given in the hypothesis of the theorem, and note that
$k=hm^{d-1}$
, with h given in the hypothesis of the theorem, and note that
![]() $k\leq M$
, because
$k\leq M$
, because
![]() $h<m/2$
. Partition the set of all children of P into two collections:
$h<m/2$
. Partition the set of all children of P into two collections:
Writing
![]() $\operatorname{\mathrm{vol}}\nolimits (P_k)/\operatorname{\mathrm{vol}}\nolimits (P)=\delta $
, we have
$\operatorname{\mathrm{vol}}\nolimits (P_k)/\operatorname{\mathrm{vol}}\nolimits (P)=\delta $
, we have
 $$ \begin{align*} \sum_{Q\in\operatorname{\mathsf{Child}}\nolimits(P)} \omega(Q)^{1/2}&(\operatorname{\mathrm{vol}}\nolimits Q)^{1/2} = \sum_{Q\in\mathcal{A}} \omega(Q)^{1/2}(\operatorname{\mathrm{vol}}\nolimits Q)^{1/2} +\sum_{Q\in \mathcal{B}} \omega(Q)^{1/2}(\operatorname{\mathrm{vol}}\nolimits Q)^{1/2}\\ &\leq \omega(A_1\cup\dots\cup A_k)^{1/2}\left(\textstyle\sum_{Q\in \mathcal{A}}\operatorname{\mathrm{vol}}\nolimits Q\right)^{1/2} + \omega(P_k)^{1/2}(\operatorname{\mathrm{vol}}\nolimits P_k)^{1/2}\\ &\leq \left((1-\delta)^{1/2}+\delta^{1/2}\eta^{-1/2}(1-\eta)^{k/2}\right)\omega(P)^{1/2}(\operatorname{\mathrm{vol}}\nolimits P)^{1/2},\end{align*} $$
$$ \begin{align*} \sum_{Q\in\operatorname{\mathsf{Child}}\nolimits(P)} \omega(Q)^{1/2}&(\operatorname{\mathrm{vol}}\nolimits Q)^{1/2} = \sum_{Q\in\mathcal{A}} \omega(Q)^{1/2}(\operatorname{\mathrm{vol}}\nolimits Q)^{1/2} +\sum_{Q\in \mathcal{B}} \omega(Q)^{1/2}(\operatorname{\mathrm{vol}}\nolimits Q)^{1/2}\\ &\leq \omega(A_1\cup\dots\cup A_k)^{1/2}\left(\textstyle\sum_{Q\in \mathcal{A}}\operatorname{\mathrm{vol}}\nolimits Q\right)^{1/2} + \omega(P_k)^{1/2}(\operatorname{\mathrm{vol}}\nolimits P_k)^{1/2}\\ &\leq \left((1-\delta)^{1/2}+\delta^{1/2}\eta^{-1/2}(1-\eta)^{k/2}\right)\omega(P)^{1/2}(\operatorname{\mathrm{vol}}\nolimits P)^{1/2},\end{align*} $$
where the first inequality holds by Cauchy–Schwarz. To find the value of
![]() $\delta $
in terms of the parameters n, m, and h, write
$\delta $
in terms of the parameters n, m, and h, write
 $$ \begin{align*}\delta=\frac{\operatorname{\mathrm{vol}}\nolimits P_k}{\operatorname{\mathrm{vol}}\nolimits P} = \frac{(m^d-2k)^n}{m^{dn}}=\left(1-\frac{2k}{m^d}\right)^n =\left(1-\frac{2h}{m}\right)^n.\end{align*} $$
$$ \begin{align*}\delta=\frac{\operatorname{\mathrm{vol}}\nolimits P_k}{\operatorname{\mathrm{vol}}\nolimits P} = \frac{(m^d-2k)^n}{m^{dn}}=\left(1-\frac{2k}{m^d}\right)^n =\left(1-\frac{2h}{m}\right)^n.\end{align*} $$
We have shown that
where
by (4.2).
Conclusion. By (4.8), (4.9), and (4.13), the harmonic measure
![]() $\omega =\omega ^X_{\Omega }$
of
$\omega =\omega ^X_{\Omega }$
of
![]() $\Omega $
satisfies the hypothesis of Lemma 2.2. Therefore,
$\Omega $
satisfies the hypothesis of Lemma 2.2. Therefore,
![]() $\overline {\dim }_H\,\omega \leq n-\lambda \rho /(\lambda +\rho )$
. As we let
$\overline {\dim }_H\,\omega \leq n-\lambda \rho /(\lambda +\rho )$
. As we let
![]() $\Omega \subsetneq \mathbb {R}^n$
be an arbitrary domain, this proves
$\Omega \subsetneq \mathbb {R}^n$
be an arbitrary domain, this proves
![]() $b_n\geq \lambda \rho /(\lambda +\rho )$
.
$b_n\geq \lambda \rho /(\lambda +\rho )$
.
Remark 4.3 Given n, m,
![]() $\eta $
, h, and d, assign
$\eta $
, h, and d, assign
Then
![]() $\gamma <V+\Pi $
, where
$\gamma <V+\Pi $
, where
![]() $\gamma $
is defined in (4.2). In particular,
$\gamma $
is defined in (4.2). In particular,
![]() $V+\Pi < 1$
implies
$V+\Pi < 1$
implies
![]() $\gamma <1$
.
$\gamma <1$
.
5 Proof of Theorem 1.1
Fix
![]() $n\geq 3$
. We first verify that
$n\geq 3$
. We first verify that
![]() $b_n>0$
. Fix a large integer
$b_n>0$
. Fix a large integer
![]() $m>\xi _m+2\sqrt {n}$
satisfying the stipulations below. By Corollary 3.2, a Bourgain-type estimate (4.1) holds with
$m>\xi _m+2\sqrt {n}$
satisfying the stipulations below. By Corollary 3.2, a Bourgain-type estimate (4.1) holds with
![]() $\alpha =C_n m^{n-2}$
and
$\alpha =C_n m^{n-2}$
and
![]() $\epsilon =1$
. Set
$\epsilon =1$
. Set
![]() $\eta =1/(3\alpha )$
,
$\eta =1/(3\alpha )$
,
![]() $h=1$
, and
$h=1$
, and
![]() $d=n$
. Then, certainly,
$d=n$
. Then, certainly,
![]() $\alpha \eta = 1/3 < (1-m^{-n})/(2-m^{-n})$
. We claim the quantity
$\alpha \eta = 1/3 < (1-m^{-n})/(2-m^{-n})$
. We claim the quantity
![]() $\gamma $
defined in (4.2) is less than
$\gamma $
defined in (4.2) is less than
![]() $1$
if m is sufficiently large. Indeed, on the one hand,
$1$
if m is sufficiently large. Indeed, on the one hand,
for large enough m. On the other hand,
![]() $\Pi =\eta ^{-1/2}(1-\eta )^{hm^{d-1}/2}=\eta ^{-1/2}(1-\eta )^{m^{n-1}/2}$
. Using the bound
$\Pi =\eta ^{-1/2}(1-\eta )^{hm^{d-1}/2}=\eta ^{-1/2}(1-\eta )^{m^{n-1}/2}$
. Using the bound
![]() $\ln (1-x)\leq -x$
for all
$\ln (1-x)\leq -x$
for all
![]() $0\leq x<1$
, we see that
$0\leq x<1$
, we see that
 $$ \begin{align*}\ln \Pi \leq \frac{1}{2}\ln(3C_n) + \frac{1}{2}(n-2)\ln(m) - \frac{m^{n-1}}{6C_n m^{n-2}}\rightarrow-\infty\quad\text{as}\ m\rightarrow\infty. \end{align*} $$
$$ \begin{align*}\ln \Pi \leq \frac{1}{2}\ln(3C_n) + \frac{1}{2}(n-2)\ln(m) - \frac{m^{n-1}}{6C_n m^{n-2}}\rightarrow-\infty\quad\text{as}\ m\rightarrow\infty. \end{align*} $$
Hence,
![]() $\Pi <1/2$
if m is sufficiently large. Thus,
$\Pi <1/2$
if m is sufficiently large. Thus,
![]() $\gamma <V+\Pi <1$
if m is sufficiently large. Therefore,
$\gamma <V+\Pi <1$
if m is sufficiently large. Therefore,
![]() $b_n>0$
by Theorem 4.1.
$b_n>0$
by Theorem 4.1.
Now, suppose that
![]() $n\geq n_{1/3}$
, where
$n\geq n_{1/3}$
, where
![]() $n_{1/3}$
is given by Corollary 3.3. Aiming for a quantitative lower bound on
$n_{1/3}$
is given by Corollary 3.3. Aiming for a quantitative lower bound on
![]() $b_n$
that is valid for all sufficiently large n, we may increase the value of n as convenient. Set
$b_n$
that is valid for all sufficiently large n, we may increase the value of n as convenient. Set
![]() $m=n$
. By Corollary 3.3, a Bourgain-type estimate (4.1) holds with
$m=n$
. By Corollary 3.3, a Bourgain-type estimate (4.1) holds with
![]() $\alpha =(1/3)(n\sqrt {2\pi e})^{n-2}$
and
$\alpha =(1/3)(n\sqrt {2\pi e})^{n-2}$
and
![]() $\epsilon =1/2$
. Set
$\epsilon =1/2$
. Set
![]() $\eta =(n\sqrt {2\pi e})^{-(n-2)}$
, which ensures that
$\eta =(n\sqrt {2\pi e})^{-(n-2)}$
, which ensures that
![]() $\alpha \eta =1/3<(1-m^{-n})/(2-m^{-n})$
. Set
$\alpha \eta =1/3<(1-m^{-n})/(2-m^{-n})$
. Set
![]() $h=1$
and
$h=1$
and
![]() $d=2n-3$
. On the one hand,
$d=2n-3$
. On the one hand,
On the other hand,
![]() $\Pi =\eta ^{-1/2}(1-\eta )^{n^{2n-4}/2}$
satisfies
$\Pi =\eta ^{-1/2}(1-\eta )^{n^{2n-4}/2}$
satisfies
 $$ \begin{align*} \ln\Pi &\leq \frac{1}{2}(n-2)\ln(n\sqrt{2\pi e})-\frac{1}{2}n^{2n-4}(n\sqrt{2\pi e})^{-(n-2)}\\ &=\frac{1}{2}(n-2)\ln(n\sqrt{2\pi e})-\frac{1}{2}\left(\frac{n}{\sqrt{2\pi e}}\right)^{n-2}. \end{align*} $$
$$ \begin{align*} \ln\Pi &\leq \frac{1}{2}(n-2)\ln(n\sqrt{2\pi e})-\frac{1}{2}n^{2n-4}(n\sqrt{2\pi e})^{-(n-2)}\\ &=\frac{1}{2}(n-2)\ln(n\sqrt{2\pi e})-\frac{1}{2}\left(\frac{n}{\sqrt{2\pi e}}\right)^{n-2}. \end{align*} $$
As the latter expression tends to
![]() $-\infty $
as n grows, we see that
$-\infty $
as n grows, we see that
![]() $\Pi <0.07$
for large n. Thus,
$\Pi <0.07$
for large n. Thus,
![]() $\gamma <V+\Pi < 0.9998$
and
$\gamma <V+\Pi < 0.9998$
and
![]() $\lambda \geq -\ln (0.9998)/\ln (n)$
for all sufficiently large n. By Theorem 4.1,
$\lambda \geq -\ln (0.9998)/\ln (n)$
for all sufficiently large n. By Theorem 4.1,
![]() $b_n\geq \lambda \rho /(\lambda +\rho )$
, where
$b_n\geq \lambda \rho /(\lambda +\rho )$
, where
![]() $\rho =0.914186(1-1/3)(1-n^{-n})n^{-2n(n-1)}/\ln (n)$
. Since
$\rho =0.914186(1-1/3)(1-n^{-n})n^{-2n(n-1)}/\ln (n)$
. Since
![]() $\rho $
is substantially smaller than
$\rho $
is substantially smaller than
![]() $\lambda $
for large n, it follows that
$\lambda $
for large n, it follows that
![]() $b_n\approx \rho $
. In particular, since
$b_n\approx \rho $
. In particular, since
![]() $0.914186(2/3)(1-n^{-n})>0.6$
, we may conclude that
$0.914186(2/3)(1-n^{-n})>0.6$
, we may conclude that
![]() $b_n\geq 0.6 n^{-2n(n-1)}/\ln (n)$
for all sufficiently large n. Therefore, since
$b_n\geq 0.6 n^{-2n(n-1)}/\ln (n)$
for all sufficiently large n. Therefore, since
![]() $b_n>0$
for all
$b_n>0$
for all
![]() $n\geq 3$
, the theorem holds: there exists
$n\geq 3$
, the theorem holds: there exists
![]() $c>0$
such that
$c>0$
such that
![]() $b_n\geq c\, n^{-2n(n-1)}/\ln (n)$
for all
$b_n\geq c\, n^{-2n(n-1)}/\ln (n)$
for all
![]() $n\geq 3$
.
$n\geq 3$
.
Remark 5.1 For the large n case, one could also choose
![]() $d=n-1+\theta (n-2)$
for any
$d=n-1+\theta (n-2)$
for any
![]() $\theta>0$
by making n large enough depending on
$\theta>0$
by making n large enough depending on
![]() $\theta $
. For simplicity, we chose
$\theta $
. For simplicity, we chose
![]() $\theta =1$
.
$\theta =1$
.
6 Proof of Theorem 1.2
When
![]() $n=3$
and
$n=3$
and
![]() $m=9$
, a Bourgain-type estimate (4.1) holds with
$m=9$
, a Bourgain-type estimate (4.1) holds with
![]() $\alpha =60.8979$
and
$\alpha =60.8979$
and
![]() $\epsilon =0.000001$
by Corollary 3.4. Assign
$\epsilon =0.000001$
by Corollary 3.4. Assign
![]() $\eta =0.0046$
,
$\eta =0.0046$
,
![]() $h=3$
, and
$h=3$
, and
![]() $d=4$
. With the aid of a calculator, one can see that
$d=4$
. With the aid of a calculator, one can see that
Thus, by Theorem 4.1,
![]() $b_3 \geq \lambda \rho /(\lambda +\rho )\geq 1.452\ldots \times 10^{-15}$
. See the Appendix for details.
$b_3 \geq \lambda \rho /(\lambda +\rho )\geq 1.452\ldots \times 10^{-15}$
. See the Appendix for details.
When
![]() $n=4$
and
$n=4$
and
![]() $m=11$
, a Bourgain-type estimate (4.1) holds with
$m=11$
, a Bourgain-type estimate (4.1) holds with
![]() $\alpha =1660.53$
by Corollary 3.5. When
$\alpha =1660.53$
by Corollary 3.5. When
![]() $\eta =0.00026$
,
$\eta =0.00026$
,
![]() $h=4$
, and
$h=4$
, and
![]() $d=5$
, one may check that
$d=5$
, one may check that
![]() $\gamma <0.9995$
. Thus, by Theorem 4.1,
$\gamma <0.9995$
. Thus, by Theorem 4.1,
![]() $b_4\geq \lambda \rho /(\lambda +\rho )\geq 2.199\ldots \times 10^{-26}$
. Once again, see the Appendix.
$b_4\geq \lambda \rho /(\lambda +\rho )\geq 2.199\ldots \times 10^{-26}$
. Once again, see the Appendix.
Remark 6.1 The authors do not claim that these bounds are sharp, but do believe that they are likely close to what the method can prove without further improvements to (3.2) or a more complicated case analysis in the proof of Theorem 4.1. Another small optimization available is to use Hölder’s inequality with conjugate exponents depending on
![]() $m,\eta ,h,d$
instead of the Cauchy–Schwarz inequality and
$m,\eta ,h,d$
instead of the Cauchy–Schwarz inequality and
![]() $p=q=1/2$
in the statement and proof of Lemma 2.2 and in the definition of
$p=q=1/2$
in the statement and proof of Lemma 2.2 and in the definition of
![]() $\gamma $
and the proof of Theorem 4.1.
$\gamma $
and the proof of Theorem 4.1.
7 Coda
The story is far from over. Now that explicit lower bounds on
![]() $b_3$
and
$b_3$
and
![]() $b_4$
and asymptotic lower bounds on
$b_4$
and asymptotic lower bounds on
![]() $b_n$
are known, one can test new methods and estimates against Bourgain’s method. The authors invite further activity to improve their estimates on (or compute!) the dimension of harmonic measure in
$b_n$
are known, one can test new methods and estimates against Bourgain’s method. The authors invite further activity to improve their estimates on (or compute!) the dimension of harmonic measure in
![]() $\mathbb {R}^n$
,
$\mathbb {R}^n$
,
![]() $n\geq 3$
.
$n\geq 3$
.
Table 1: Bounding Bourgain’s constant for harmonic measure:
![]() $b_n\geq \lambda \rho /(\lambda +\rho )\approx \rho $
when
$b_n\geq \lambda \rho /(\lambda +\rho )\approx \rho $
when
![]() $\rho \ll \lambda $
. Bold entries indicate optimal parameters.
$\rho \ll \lambda $
. Bold entries indicate optimal parameters.

A Wolfram Language code for estimating
 $b_3$
$b_3$
We wrote the following code in Mathematica 13 to estimate
![]() $b_3$
using Theorem 4.1 and Corollary 3.4. See Table 1 for a record of outputs. For each fixed
$b_3$
using Theorem 4.1 and Corollary 3.4. See Table 1 for a record of outputs. For each fixed
![]() $m\geq 5$
, the parameters
$m\geq 5$
, the parameters
![]() $\eta $
, h, and d were optimized by hand. To maximize
$\eta $
, h, and d were optimized by hand. To maximize
![]() $\rho $
, the first priority is to minimize d. To rule out small values of d, take
$\rho $
, the first priority is to minimize d. To rule out small values of d, take
![]() $\eta \approx \alpha ^{-1}(1-m^{-3})/(2-m^{-3})$
and check that
$\eta \approx \alpha ^{-1}(1-m^{-3})/(2-m^{-3})$
and check that
![]() $\gamma>1$
for each integer
$\gamma>1$
for each integer
![]() $1\leq h<m/2$
. Once the optimal value of the integer d is identified, the second priority is to minimize the real-valued parameter
$1\leq h<m/2$
. Once the optimal value of the integer d is identified, the second priority is to minimize the real-valued parameter
![]() $\eta $
. Using the current best guess for
$\eta $
. Using the current best guess for
![]() $\eta $
(keeping
$\eta $
(keeping
![]() $\gamma <1$
), adjust h to minimize
$\gamma <1$
), adjust h to minimize
![]() $\gamma $
. One can then test the value of
$\gamma $
. One can then test the value of
![]() $\gamma $
against smaller values of
$\gamma $
against smaller values of
![]() $\eta $
. If
$\eta $
. If
![]() $\gamma <1$
for some smaller value of
$\gamma <1$
for some smaller value of
![]() $\eta $
, update the best guess for
$\eta $
, update the best guess for
![]() $\eta $
and repeat (adjust h, test smaller values of
$\eta $
and repeat (adjust h, test smaller values of
![]() $\eta $
). Halt the search for
$\eta $
). Halt the search for
![]() $\eta $
once all smaller values of
$\eta $
once all smaller values of
![]() $\eta $
(up to some predetermined number of decimals) yield
$\eta $
(up to some predetermined number of decimals) yield
![]() $\gamma>1$
. Use the values of
$\gamma>1$
. Use the values of
![]() $\lambda $
and
$\lambda $
and
![]() $\rho $
associated with m,
$\rho $
associated with m,
![]() $\eta $
, h, and d to bound
$\eta $
, h, and d to bound
![]() $b_3$
from below by
$b_3$
from below by
![]() $\lambda \rho /(\lambda +\rho )$
.
$\lambda \rho /(\lambda +\rho )$
.

The code used to estimate
![]() $b_4$
(omitted) is similar. It can be reproduced by modifying the definition of bgAlpha using Corollary 3.5 instead of Corollary 3.4 and changing
$b_4$
(omitted) is similar. It can be reproduced by modifying the definition of bgAlpha using Corollary 3.5 instead of Corollary 3.4 and changing
![]() $n=3$
to
$n=3$
to
![]() $n=4$
in the definitions of bgMaxEta, bgV, bgEtaProd, and bgRho.
$n=4$
in the definitions of bgMaxEta, bgV, bgEtaProd, and bgRho.
Acknowledgment
The authors thank Max Engelstein for bringing the work [Reference Grebenkov, Lebedev, Filoche and Sapoval16] by Grebenkov et al. and [Reference Filoche, Grebenkov, Andrade and Sapoval14] by Filoche et al. to their attention. The authors would also like to thank Polina Perstneva and several anonymous referees for their critiques of an earlier draft of the paper.