Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-29T04:43:03.645Z Has data issue: false hasContentIssue false
  • English
  • Français

Lusternik-Schnirelmann Category and Algebraic R-Local Homotopy Theory

Published online by Cambridge University Press:  20 November 2018

H. Scheerer  and
D. Tanré
H. Scheerer
Affiliation:
Freie Universität Berlin, Mathematisches Institut, Arnimallee 2–6, D-14195 Berlin, Germany
D. Tanré
Affiliation:
U.F.R. de Mathématiques, URA CNRS 0751 D, Université des Sciences et Technologies de Lille-Flandres-Artois59655 Villeneuve d’Ascq Cedex, France
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we define the notion of 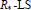${{R}_{*}}\text{-LS}$ category associated to an increasing system of subrings of $\mathbb{Q}$ and we relate it to the usual 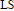$\text{LS}$-category. We also relate it to the invariant introduced by Félix and Lemaire in tame homotopy theory, in which case we give a description in terms of Lie algebras and of cocommutative coalgebras, extending results of Lemaire-Sigrist and Félix-Halperin.

Keywords

55P5055P62
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 50 , Issue 4 , 01 August 1998 , pp. 845 - 862
Copyright
Copyright © Canadian Mathematical Society 1998

References

1. Anick, D., R-local homotopy theory. Lecture Notes in Math. 1418, Springer-Verlag, 1990. 78–85.Google Scholar
2. Baues, H., Algebraic homotopy. Cambridge Stud. Adv. Math. 15(1983).Google Scholar
3. Doeraene, J.-P., LS-category in a model category. J. Pure Appl. Algebra 84(1993), 215–261.Google Scholar
4. Doeraene, J.-P. and Tanré, D., Axiome du cube et foncteurs de Quillen. Ann. Inst. Fourier. 45(1995), 1061–1077.Google Scholar
5. Dwyer, W. G., Tame homotopy theory. Topology 18(1979), 321–338.Google Scholar
6. Dwyer, W. G., The tame homotopy groups of a suspension. Geometric Applications in Homotopy Theory II, Proceedings, Evanston, 1977. Lecture Notes in Math. 658, Springer-Verlag, 1978. 165–168.Google Scholar
7. Félix, Y. and Halperin, S., RationalLS-category and its applications. Trans. Amer.Math. Soc. 273(1982), 1–37.Google Scholar
8. Félix, Y. and Lemaire, J.-M., On the mapping theorem for Lusternik-Schnirelmann category. Topology 24(1985), 41–43; 27(1987), 177.Google Scholar
9. Félix, Y., On the mapping theorem for Lusternik-Schnirelmann category II. Canad. J. Math. XL(1988), 1389–1398.Google Scholar
10. Gilbert, W. J., Some examples for weak category and conilpotency. Illinois J. Math. 12(1968), 421–432.Google Scholar
11. Hess, K., A proof of Ganea's conjecture for rational spaces. Topology 30(1991), 205–214.Google Scholar
12. Husemoller, D., Moore, J. C. and Stasheff, J., Differential homological algebra and homogeneous spaces. J. Pure Appl. Algebra 5(1974), 113–185.Google Scholar
13. James, I. M., On category in the sense of Lusternik-Schnirelmann. Topology 17(1978), 331–348.Google Scholar
14. Jessup, B., RationalLS category and a conjecture of Ganea. J. Pure Appl. Algebra 65(1990), 45–56.Google Scholar
15. Lemaire, J.-M. and Sigrist, F., Sur les invariants d’homotopie rationnelle liés à laLS-catégorie.Comment. Math. Helv. 56(1981), 103–122.Google Scholar
16. Lusternik, L. and Schnirelmann, L., Méthodes topologiques dans les problèmes variationnels. Hermann, Paris, 1934.Google Scholar
17. Scheerer, H. and Tanré, D., R-local homotopy theory. Bull. London Math. Soc. 22(1990), 591–598.Google Scholar
18. Scheerer, H., The Milnor-Moore theorem in tame homotopy theory. Manuscripta Math. 70(1991), 227–246.Google Scholar
19. Scheerer, H., Exploring W. G. Dwyer's tame homotopy theory. Publ. Matemàtiques 35(1991), 375–402.Google Scholar
20., Homotopie modérée et tempérée avec les coalgèbres. Applications aux espaces fonctionnels. Arch.Math. 59(1992), 130–145.Google Scholar
21., Fibrations àla Ganea. Bull. Soc. Math. Belg. 4(1997), 333–353.Google Scholar