Article contents
MAD Saturated Families and SANE Player
Published online by Cambridge University Press: 20 November 2018
Abstract
We throw some light on the question: is there a MAD family (a maximal family of infinite subsets of 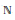 $\mathbb{N}$, the intersection of any two is finite) that is saturated (=completely separable i.e., any
$\mathbb{N}$, the intersection of any two is finite) that is saturated (=completely separable i.e., any 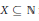 $X\,\subseteq \,\mathbb{N}$ is included in a finite union of members of the family or includes a member (and even continuum many members) of the family). We prove that it is hard to prove the consistency of the negation:
$X\,\subseteq \,\mathbb{N}$ is included in a finite union of members of the family or includes a member (and even continuum many members) of the family). We prove that it is hard to prove the consistency of the negation:
(i) if 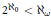 ${{2}^{{{\aleph }_{0}}}}\,<\,{{\aleph }_{\omega }}$, then there is such a family;
${{2}^{{{\aleph }_{0}}}}\,<\,{{\aleph }_{\omega }}$, then there is such a family;
(ii) if there is no such family, then some situation related to pcf holds whose consistency is large (and if 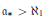 ${{a}_{*}}\,>\,{{\aleph }_{1}}$ even unknown);
${{a}_{*}}\,>\,{{\aleph }_{1}}$ even unknown);
(iii) if, e.g., there is no inner model with measurables, then there is such a family.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2011
References
- 13
- Cited by


