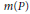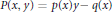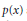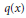Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Smyth, Chris J.
2002.
An explicit formula for the Mahler measure of a family of 3-variable polynomials.
Journal de théorie des nombres de Bordeaux,
Vol. 14,
Issue. 2,
p.
683.
Lalı́n, Matilde N.
2003.
Some examples of Mahler measures as multiple polylogarithms.
Journal of Number Theory,
Vol. 103,
Issue. 1,
p.
85.
Vandervelde, S.
2003.
A formula for the Mahler measure of axy+bx+cy+d.
Journal of Number Theory,
Vol. 100,
Issue. 1,
p.
184.
Lal�n, Matilde
2004.
Mahler Measure and Volumes in Hyperbolic Space.
Geometriae Dedicata,
Vol. 107,
Issue. 1,
p.
211.
Champanerkar, Abhijit
and
Kofman, Ilya
2005.
On the Mahler measure of Jones polynomials under twisting.
Algebraic & Geometric Topology,
Vol. 5,
Issue. 1,
p.
1.
Lalín, Matilde N.
2006.
Mahler measure of some n-variable polynomial families.
Journal of Number Theory,
Vol. 116,
Issue. 1,
p.
102.
Lalín, Matilde N.
2007.
An algebraic integration for Mahler measure.
Duke Mathematical Journal,
Vol. 138,
Issue. 3,
Gon, Yasuro
Kurokawa, Nobushige
and
Oyanagi, Hideo
2007.
Multiple q-Mahler measures and zeta functions.
Journal of Number Theory,
Vol. 124,
Issue. 2,
p.
328.
Vandervelde, Sam
2008.
The Mahler measure of parametrizable polynomials.
Journal of Number Theory,
Vol. 128,
Issue. 8,
p.
2231.
Lalín, Matilde N.
2008.
Mahler measures and computations with regulators.
Journal of Number Theory,
Vol. 128,
Issue. 5,
p.
1231.
Dijkgraaf, R.
and
Fuji, H.
2009.
The volume conjecture and topological strings.
Fortschritte der Physik,
Vol. 57,
Issue. 9,
p.
825.
Benferhat, Leila
2010.
Mahler Measure and Modular Elliptic Surfaces.
Quaestiones Mathematicae,
Vol. 33,
Issue. 2,
p.
231.
Harada, Shinya
2014.
Hasse–Weil zeta functions ofSL2-character varieties of arithmetic two-bridge link complements.
Finite Fields and Their Applications,
Vol. 27,
Issue. ,
p.
115.
Dimofte, Tudor
Gaiotto, Davide
and
Gukov, Sergei
2014.
Gauge Theories Labelled by Three-Manifolds.
Communications in Mathematical Physics,
Vol. 325,
Issue. 2,
p.
367.
Khoi, Vu The
2014.
Seifert volumes and dilogarithm identities.
Journal of Knot Theory and Its Ramifications,
Vol. 23,
Issue. 05,
p.
1450025.
Dimofte, Tudor
Gabella, Maxime
and
Goncharov, Alexander B.
2016.
K-decompositions and 3d gauge theories.
Journal of High Energy Physics,
Vol. 2016,
Issue. 11,
Champanerkar, Abhijit
Kofman, Ilya
and
Lalín, Matilde
2019.
Mahler measure and the Vol‐Det Conjecture.
Journal of the London Mathematical Society,
Vol. 99,
Issue. 3,
p.
872.
Guilloux, Antonin
and
Marché, Julien
2021.
Volume function and Mahler measure of exact polynomials.
Compositio Mathematica,
Vol. 157,
Issue. 4,
p.
809.
Gu, Jarry
and
Lalín, Matilde
2021.
The Mahler measure of a three-variable family and an application to the Boyd–Lawton formula.
Research in Number Theory,
Vol. 7,
Issue. 1,
Bao, Jiakang
He, Yang-Hui
and
Zahabi, Ali
2022.
Mahler Measure for a Quiver Symphony.
Communications in Mathematical Physics,
Vol. 394,
Issue. 2,
p.
573.