Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-10T21:45:37.115Z Has data issue: false hasContentIssue false
  • English
  • Français

Marginals with Finite Repulsive Cost

Part of: Existence theories Optimality conditions

Published online by Cambridge University Press:  07 May 2019

Ugo Bindini
Ugo Bindini*
Affiliation:
Scuola Normale Superiore, Piazza dei Cavalieri, 7, 56127 Pisa, Italy Email: ugo.bindini@sns.it
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider a multimarginal transport problem with repulsive cost, where the marginals are all equal to a fixed probability 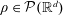$\unicode[STIX]{x1D70C}\in {\mathcal{P}}(\mathbb{R}^{d})$. We prove that, if the concentration of 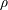$\unicode[STIX]{x1D70C}$ is less than 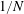$1/N$, then the problem has a solution of finite cost. The result is sharp, in the sense that there exists 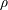$\unicode[STIX]{x1D70C}$ with concentration 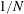$1/N$ for which the cost is infinite.

Keywords

multi-marginaloptimal transportrepulsive cost

MSC classification

Primary: 49J10: Free problems in two or more independent variables
Secondary: 49K10: Free problems in two or more independent variables
Type
Article
Information
Canadian Journal of Mathematics , Volume 72 , Issue 2 , April 2020 , pp. 373 - 391
Copyright
© Canadian Mathematical Society 2018

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ambrosio, L., Gigli, N., and Savaré, G., Gradient flows in metric spaces and in the space of probability measures. Birkhäuser, Verlag, Basel, 2005.Google Scholar
Bindini, U. and De Pascale, L., Optimal transport with Coulomb cost and the semiclassical limit of density functional theory. J. Éc. polytech. Math. 4(2017), 909–934. https://doi.org/10.5802/jep.59.Google Scholar
Buttazzo, G., Champion, T., and De Pascale, L., Continuity and estimates for multimarginal optimal transportation problems with singular costs. Appl. Math. Optim. 78(2018), 185–200. https://doi.org/10.1007/s00245-017-9403-7.Google Scholar
Buttazzo, G., De Pascale, L., and Gori-Giorgi, P., Optimal-transport formulation of electronic density-functional theory. Phys. Rev. A 85(2012), 062502.Google Scholar
Colombo, M., De Pascale, L., and Di Marino, S., Multimarginal optimal transport maps for 1-dimensional repulsive costs. Canad. J. Math. 67(2015), 350–368. https://doi.org/10.4153/CJM-2014-011-x.Google Scholar
Colombo, M. and Di Marino, S., Equality between Monge and Kantorovich multimarginal problems with Coulomb cost. Ann. Mat. Pura Appl. 194(2015), 307–320. https://doi.org/10.1007/s10231-013-0376-0.Google Scholar
Cotar, C., Friesecke, G., and Klüppelberg, C., Density functional theory and optimal transportation with Coulomb cost. Comm. Pure Appl. Math. 66(2013), 548–599. https://doi.org/10.1002/cpa.21437.Google Scholar
Cotar, C., Friesecke, G., and Klüppelberg, C., Smoothing of transport plans with fixed marginals and rigorous semiclassical limit of the Hohenberg-Kohn functional. Arch. Ration. Mech. Anal. 228(2018), 891–922. https://doi.org/10.1007/s00205-017-1208-y.Google Scholar
De Pascale, L., Optimal transport with Coulomb cost. Approximation and duality. ESAIM Math. Model. Numer. Anal. 49(2015), 1643–1657. https://doi.org/10.1051/m2an/2015035.Google Scholar
Di Marino, S., Gerolin, A., and Nenna, L., Optimal transportation theory for repulsive costs. In: Topoligal Optimization and Optimal Transport in the Applied Sciences. Radon Series on Computational and Applied Mathematics, 17, De Gruyter, Berli-Boston, 2017, pp. 204–256.. https://doi.org/10.1515/9783110430417-010.Google Scholar
Gangbo, W. and Swiech, A., Optimal maps for the multidimensional Monge–Kantorovich problem. Comm. Pure Appl. Math. 51(1998), 23–45. http://dx.doi.org/10.1002/(SICI)1097-0312(199801)51:1¡23::AID-CPA2¿3.0.CO;2-H.Google Scholar
Gori-Giorgi, P. and Seidl, M., Density functional theory for strongly-interacting electrons: perspectives for physics and chemistry. Phys. Chem. Chem. Phys. 12(2010), 14405–14419.Google Scholar
Gori-Giorgi, P., Seidl, M., and Vignale, G., Density-functional theory for strongly interacting electrons. Phys. Rev. Lett. 103(2009), 166402–166405.Google Scholar
Hohenberg, P. and Kohn, W., Inhomogeneous electron gas. Phys. Rev. 136(1964), B864–B871.Google Scholar
Levy, M., Universal variational functionals of electron densities, first-order density matrices, and natural spin-orbitals and solution of the v-representability problem. Proc. Nat. Acad. Sci. USA 76(1979), 6062–6065. https://doi.org/10.1073/pnas.76.12.6062.Google Scholar
Lewin, M., Semi-classical limit of the Levy-Lieb functional in density functional theory. C. R. Math. Acad. Sci. Paris 356(2018), no. 4, 449–455. https://doi.org/10.1016/j.crma.2018.03.002.Google Scholar
Lieb, E. H., Density functionals for Coulomb systems. Internat. J. Quantum Chemistry 24(1983), 243–277. https://doi.org/10.1002/qua.560240302.Google Scholar
Pass, B., On the local structure of optimal measures in the multi-marginal optimal transportation problem. Calc. Var. Partial Differential Equations 43(2012), 529–536. https://doi.org/10.1007/s00526-011-0421-z.Google Scholar