No CrossRef data available.
Article contents
Meridional rank and bridge number of knotted 2-spheres
Published online by Cambridge University Press: 27 December 2023
Abstract
The meridional rank conjecture asks whether the bridge number of a knot in 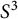 $S^3$ is equal to the minimal number of meridians needed to generate the fundamental group of its complement. In this paper, we investigate the analogous conjecture for knotted spheres in
$S^3$ is equal to the minimal number of meridians needed to generate the fundamental group of its complement. In this paper, we investigate the analogous conjecture for knotted spheres in 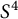 $S^4$. Towards this end, we give a construction to produce classical knots with quotients sending meridians to elements of any finite order in Coxeter groups and alternating groups, which detect their meridional ranks. We establish the equality of bridge number and meridional rank for these knots and knotted spheres obtained from them by twist-spinning. On the other hand, we show that the meridional rank of knotted spheres is not additive under connected sum, so that either bridge number also collapses, or meridional rank is not equal to bridge number for knotted spheres.
$S^4$. Towards this end, we give a construction to produce classical knots with quotients sending meridians to elements of any finite order in Coxeter groups and alternating groups, which detect their meridional ranks. We establish the equality of bridge number and meridional rank for these knots and knotted spheres obtained from them by twist-spinning. On the other hand, we show that the meridional rank of knotted spheres is not additive under connected sum, so that either bridge number also collapses, or meridional rank is not equal to bridge number for knotted spheres.
- Type
- Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of Canadian Mathematical Society
Footnotes
The first author was supported by the Max Planck Institute for Mathematics and the NSF grant DMS-1664567 during part of this research and is currently supported by the NSF-RTG grant NSF DMS-1745670. Research conducted for this paper is supported by the Pacific Institute for the Mathematical Sciences (PIMS). The research and findings may not reflect those of the Institute.



