Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-27T09:11:42.107Z Has data issue: false hasContentIssue false
  • English
  • Français

Moments of the Rank of Elliptic Curves

Published online by Cambridge University Press:  20 November 2018

Steven J. Miller  and
Siman Wong
Steven J. Miller
Affiliation:
Department of Mathematics and Statistics, Williams College, Williamstown, MA 01267, U.S.A. email: siman@math.umass.edu
Siman Wong
Affiliation:
Department of Mathematics and Statistics, University of Massachusetts, Amherst, MA 01003-4515, U.S.A email: sjm1@williams.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Fix an elliptic curve 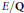$E/\mathbf{Q}$and assume the Riemann Hypothesis for the $L$-function 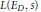$L({{E}_{D}},\,s)$ for every quadratic twist 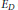${{E}_{D}}$ of 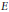$E$ by 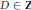$D\,\in \,\mathbf{Z}$. We combine Weil's explicit formula with techniques of Heath-Brown to derive an asymptotic upper bound for the weighted moments of the analytic rank of 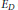${{E}_{D}}$. We derive from this an upper bound for the density of low-lying zeros of 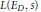$L({{E}_{D}},\,s)$ that is compatible with the randommatrixmodels of Katz and Sarnak. 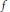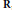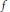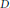We also show that for any unbounded increasing function $f$ on $\mathbf{R}$, the analytic rank and (assuming in addition the Birch and Swinnerton-Dyer conjecture) the number of integral points of ${{E}_{D}}$ are less than $f(D)$ for almost all $D$.

Keywords

11G0511G40elliptic curveexplicit formulaintegral pointlow-lying zerosquadratic twistrank
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 64 , Issue 1 , 01 February 2012 , pp. 151 - 182
Copyright
Copyright © Canadian Mathematical Society 2012

References

[1] Bektemirov, B., Mazur, B., Stein, W., and Watkins, M., Average ranks of elliptic curves: tension between data and conjecture. Bull. Amer. Math. Soc. (N. S.) 44(2007), no. 2, 233-254. http://dx. doi. org/10.1090/S0273-0979-07-01138-XGoogle Scholar
[2] Brumer, A., The average rank of elliptic curves. I. Invent. Math. 109(1992), no. 3, 445-472. http://dx. doi. org/10.1007/BF01232033Google Scholar
[3] Brumer, A. and McGuinness, O., The behavior of the Mordell-Weil group of elliptic curves. Bull. Amer. Math. Soc. (N. S.) 23(1990), no. 2, 375-382. http://dx. doi. org/10.1090/S0273-0979-1990-15937-3Google Scholar
[4] Conrey, J. B., L-Functions and random matrices. In: Mathematics unlimited—2001 and beyond, Springer-Verlag, Berlin, 2001, pp. 331-352.Google Scholar
[5] Conrey, J. B., Pokharel, A., Rubinstein, M. O., and Watkins, M., Secondary terms in the number of vanishings of quadratic twists of elliptic curve L-functions. In: Ranks of elliptic curves and random matrix theory, London Math. Soc. Lecture Note Ser., 341, Cambridge University Press, Cambridge, 2007, pp. 215-232.Google Scholar
[6] Davenport, H., Multiplicative number theory. Third ed., Graduate Texts in Mathematics, 74, Springer-Verlag, New York, 2000.Google Scholar
[7] David, C., Fearnley, J., and Kisilevsky, H., On the vanishing of twisted L-functions of elliptic curves. Experiment. Math. 13(2004), no. 2, 185-198.Google Scholar
[8] Duenez, E. and Miller, S. J., The effect of convolving families of L-functions on the underlying group symmetries. Proc. London Math. Soc. 99(2009), no. 3, 787-820. doi:10.1112/plms/pdp018 http://dx. doi. org/10.1112/plms/pdp018Google Scholar
[9] Dusart, P., The k-th prime is greater than k(ln k + ln ln k — 1) for k _ 2. Math. Comp. 68(1999), no. 225, 411-415. http://dx. doi. org/10.1090/S0025-5718-99-01037-6Google Scholar
[10] Fermigier, S., Zéros des fonctions L de courbes elliptiques. Experiment. Math. 1(1992), no. 2, 167-173.Google Scholar
[11] Fermigier, S., Étude expérimentale du rang de familles de courbes elliptiques sur Q . Experiment. Math. 5(1996), no. 2, 119-130.Google Scholar
[12] Goes, J. and Miller, S. J., Towards an ‘average’ version of the Birch and Swinnerton-Dyer conjecture. J. Number Theory 130(2010), no. 10, 2341-2358. http://dx. doi. org/10.1016/j. jnt.2010.04.002Google Scholar
[13] Goldfeld, D., Conjectures on elliptic curves over quadratic fields. In: Number theory, Carbondale 1979 (Proc. Southern Illinois Conf., Southern Illinois Univ., Carbondale, Ill., 1979), Lecture Notes in Math., 751, Springer-Verlag, Berlin, 1979, pp. 108-118.Google Scholar
[14] Heath-Brown, D. R., The average rank of elliptic curves. Duke Math. J. 122(2004), no. 3, 591-623. http://dx. doi. org/10.1215/S0012-7094-04-12235-3Google Scholar
[15] Hughes, C. P. and Rudnick, Z., Linear statistics of low-lying zeros of L-functions. Q. J. Math. 54(2003), no. 3, 309-333. http://dx. doi. org/10.1093/qmath/hag021Google Scholar
[16] Iwaniec, H. and Kowalski, E., Analytic number theory. American Mathematical Society Colloquium Publications, 53, American Mathematical Society, Providence, RI, 2004.Google Scholar
[17] Silverman, J. H., Advanced topics in the arithmetic of elliptic curves. Graduate Texts in Mathematics, 151, Springer-Verlag, New York, 1994.Google Scholar
[18] Katz, N. M., Twisted L-functions and monodromy. Annals of Mathematics Studies, 150, Princeton University Press, Princeton, NJ, 2002.Google Scholar
[19] Katz, N. M. and Sarnak, P., Random matrices, Frobenius eigenvalues, and monodromy. American Mathematical Society Colloquium Publications, 45, American Mathematical Society, Providence, RI, 1999.Google Scholar
[20] Katz, N. M. and Sarnak, P., Zeros of zeta functions and symmetry. Bull. Amer. Math. Soc. (N. S.) 36(1999), no. 1, 1-26. http://dx. doi. org/10.1090/S0273-0979-99-00766-1Google Scholar
[21] Keating, J. P. and Snaith, N. C., Random matrices and L-functions. Random matrix theory. J. Phys. A 36(2003), no. 12, 2859-2881. http://dx. doi. org/10.1088/0305-4470/36/12/301Google Scholar
[22] Kowalski, E., Elliptic curves, rank in families and random matrices. In: Ranks of elliptic curves and random matrix theory, London Mathematical Society Lecture Note Series, 341, Cambridge University Press, Cambridge, 2007, pp. 7-52.Google Scholar
[23] Kowalski, E., On the rank of quadratic twists of elliptic curves over function fields. Int. J. Number Theory 2(2006), no. 2, 267-288. http://dx. doi. org/10.1142/S1793042106000528Google Scholar
[24] Lang, S., Elliptic curves: diophantine analysis. Grundlehren der Mathematischen Wissenschaften, 231, Springer-Verlag, Berlin-New York, 1978.Google Scholar
[25] Mazur, B., Tate, J., and Teitelbaum, J., On p-adic analogues of the conjectures of Birch and Swinnerton-Dyer. Invent. Math. 84(1986), no. 1, 1-48. http://dx. doi. org/10.1007/BF01388731Google Scholar
[26] Michel, P., Rang moyen de familles de courbes elliptiques et lois de Sato-Tate. Monatsh. Math. 120(1995), no. 2, 127-136. http://dx. doi. org/10.1007/BF01585913Google Scholar
[27] Miller, S. J., One- and two-level densities for rational families of elliptic curves: evidence for the underlying group symmetries. Compos. Math. 140(2004), no. 4, 952-992. http://dx. doi. org/10.1112/S0010437X04000582Google Scholar
[28] Mestre, J. F., Formules explicites et minorations de conducteurs de variétés algébriques. Compos. Math. 58(1986), no. 2, 209-232.Google Scholar
[29] Nekovář, J., On the parity of ranks of Selmer groups. II. C. R. Acad. Sci. Paris Sér. I Math. 332(2001), no. 2, 99-104.Google Scholar
[30] Rubin, K. and Silverberg, A., Ranks of elliptic curves. Bull. Amer. Math. Soc. 39(2002), no. 4, 455-474. http://dx. doi. org/10.1090/S0273-0979-02-00952-7Google Scholar
[31] Rubinstein, M., Low-lying zeros of L-functions and random matrix theory. Duke Math. J. 109(2001), no. 1, 147-181. http://dx. doi. org/10.1215/S0012-7094-01-10916-2Google Scholar
[32] Silverman, J., The arithmetic of elliptic curves. Graduate Texts in Mathematics, 106, Springer-Verlag, New York, 1986.Google Scholar
[33] Silverman, J., A quantitative version of Siegel's theorem: integral points on elliptic curves and Catalan curves. J. Reine Angew. Math. 378(1987), 60-100. http://dx. doi. org/10.1515/crll.1987.378.60Google Scholar
[34] Tenenbaum, G., Introduction à la théorie analytique et probabiliste des nombres. Second ed., Cours Spécialisés, 1., Société Mathématique de France, Paris, 1995.Google Scholar
[35] Watkins, M., Rank distribution in a family of cubic twists. In: Ranks of elliptic curves and random matrix theory, London Math. Soc. Lecture Note Series, 341, Cambridge University Press, Cambridge, 2007.Google Scholar
[36] Young, M. P., Low-lying zeros of families of elliptic curves. J. Amer. Math. Soc. 19(2006), no. 1, 205-250. http://dx. doi. org/10.1090/S0894-0347-05-00503-5Google Scholar
[37] Zagier, D. and Kramarz, G., Numerical investigations related to the L-series of certain elliptic curves. J. Indian Math. Soc. 52(1987), 51-69.Google Scholar