No CrossRef data available.
Article contents
Monocoreflective Subcategories in General Topology
Published online by Cambridge University Press: 20 November 2018
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let 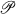 be a full subcategory of a category
be a full subcategory of a category  is said to be coreflective in
is said to be coreflective in  if for each object X in
if for each object X in 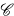 there exists an object
there exists an object 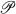 X in
X in 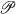 and a morphism
and a morphism 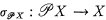 such that for each object P in
such that for each object P in 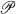 and each morphism f : P ⟶ X there exists a unique morphism
and each morphism f : P ⟶ X there exists a unique morphism 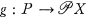 such that
such that 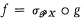 .
.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1977
References
1.
Bernstein, A. R., A new kind of compactness for topological spaces,
Fund. Math. 66 (1969/70), 185–193.Google Scholar
2.
Frohlich, O., Das Halbordnungssytem der topologischen Rdume auf einer Menge, Math. Ann. 156( 1964), 79–85.Google Scholar
3.
Gillman, L. and Jerison, M., Rings of continuous functions (Van Nostrand Princeton, N.J.
1960).Google Scholar
4.
Herrlich, H. and Strecker, G. E., Coreflective subcategories in general topology,
Fund. Math. 73 (1971), 199–218.Google Scholar
5.
Kennison, J. F., Reflective functions in general topology and elsewhere,
Trans. Amer. Math. Soc. 118 (1965), 303–315.Google Scholar
6.
Maclane, S., Categories for the working mathematician,
G. T. M. 5 (Springer-Verlag, New York, 1971).Google Scholar
7.
Porter, J. R. and Woods, R. G., Minimal extremally disconnected Hausdorff spaces, to appear, General Topology and its Applications.Google Scholar
8.
Steiner, A. K., The lattice of topologies: structure and complementation,
Trans. Amer. Math. Soc. 122 (1966), 379–398.Google Scholar
9.
Walker, R. C., The Stone-Cech compactification, Band 83 Ergebnisse der Math, und ihrer Grenz. (Springer-Verlag, New York, 1974).Google Scholar
10.
Woods, R. G., Topological extension properties,
Trans. Amer. Math. Soc. 210 (1975), 365–386.Google Scholar


