Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T18:23:31.088Z Has data issue: false hasContentIssue false
  • English
  • Français

Monoidal Functors, Acyclic Models and Chain Operads

Published online by Cambridge University Press:  20 November 2018

F. Guillén Santos ,
V. Navarro ,
P. Pascual  and
Agustí Roig
F. Guillén Santos
Affiliation:
Departament d’Àlgebra i Geometria, Universitat de Barcelona, 08007 Barcelona, Spain e-mail: fguillen@ub.edu, vicenc.navarro@ub.edu
V. Navarro
Affiliation:
Departament d’Àlgebra i Geometria, Universitat de Barcelona, 08007 Barcelona, Spain e-mail: fguillen@ub.edu, vicenc.navarro@ub.edu
P. Pascual
Affiliation:
Departament de Matemàtica Aplicada I, Universitat Politècnica de Catalunya, 08028 Barcelona, Spain e-mail: pere.pascual@upc.eduagustin.roig@upc.edu
Agustí Roig
Affiliation:
Departament de Matemàtica Aplicada I, Universitat Politècnica de Catalunya, 08028 Barcelona, Spain e-mail: pere.pascual@upc.eduagustin.roig@upc.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove that for a topological operad 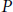$P$ the operad of oriented cubical singular chains, 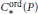$C_{*}^{^{\text{ord}}}(P)$, and the operad of simplicial singular chains, 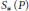${{S}_{*}}(P)$, are weakly equivalent. As a consequence, 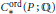$C_{*}^{^{\text{ord}}}(P;\,\mathbb{Q})$ is formal if and only if 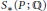${{S}_{*}}(P;\,\mathbb{Q})$ is formal, thus linking together some formality results which are spread out in the literature. The proof is based on an acyclic models theorem for monoidal functors. We give different variants of the acyclic models theorem and apply the contravariant case to study the cohomology theories for simplicial sets defined by 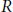$R$-simplicial differential graded algebras.

Keywords

18G8055N1018D50acyclic modelsoperadsmonoidal functorscohomology theories
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 60 , Issue 2 , 01 April 2008 , pp. 348 - 378
Copyright
Copyright © Canadian Mathematical Society 2008

References

[B95] Barr, M., Oriented singular homology Theory Appl. Categ. 1(1995), no. 1, 1–9 (electronic).Google Scholar
[B96] Barr, M., Acyclic models Canad. J. Math. 48(1996), no. 2, 258–273.Google Scholar
[B02] Barr, M., Acyclic models . CRM Monograph Series 17, American Mathematical Society, Providence, RI, 2002.Google Scholar
[BB] Barr, M. and Beck, J., Acyclic models and triples. In: Proc. Conf. Categorical Algebra, Springer, New York, 1966, pp. 336–343.Google Scholar
[BG] Bousfield, A. K. and Gugenheim, V. K. A. M., On PL de Rham theory and rational homotopy type. Mem. Amer.Math. Soc 8(1976), no. 179.Google Scholar
[C] Cartan, H., Théories cohomologiques. Invent. Math. 35(1976), 261–271.Google Scholar
[D] Dold, A., Lectures on Algebraic Topology . Die Grundlehren der Mathematischen Wissenschaften 200, Springer-Verlag, New York, 1972.Google Scholar
[DMO] Dold, A., Mac Lane, S., and Olbers, U., Projective classes and acyclic models. In: Reports of the Midwest Category Seminar. Springer, Berlin, 1967, pp. 78–91.Google Scholar
[EK] Eilenberg, S. and Kelly, G. M., Closed categories. In: Proc. Conference in Categorical Algebra, Springer, New York, 1966, pp. 421–562.Google Scholar
[EM1] Eilenberg, S. and Mac Lane, S., Acyclic models. Amer. J. Math. 75(1953), 189–199.Google Scholar
[EM2] Eilenberg, S. and Mac Lane, S., On the groups H(π, n). I. Ann. of Math. 58(1953), 55–106.Google Scholar
[FHT] Félix, Y., Halperin, S., and Thomas, J. C., Rational homotopy theory . Graduate Texts in Mathematics 205. Springer-Verlag, New York, 2001.Google Scholar
[GK] Getzler, E. and Kapranov, M., Modular operads. Compositio Math. 110(1998), no. 1, 65–126.Google Scholar
[GM] Gugenhein, V. K. A. M. and May, J. P., On the theory and applications of differential torsion products . Mem Amer.Math. Soc. 142. American Mathematical Society, Providence, RI, 1974.Google Scholar
[GMo] Gugenhein, V. K. A. M. and Moore, J. C., Acyclic models and fibre spaces. Trans. Amer.Math. Soc. 85(1957), 265–306.Google Scholar
[GN] Guillén, F. and Navarro Aznar, V., Un critère d’extension des foncteurs définis sur les schémas lisses. Publ. Math. Inst. Hautes Études Sci. 95(2002), 1–91.Google Scholar
[GNPR] Guillén Santos, F., Navarro, V., Pascual, P., and Roig, A., Moduli spaces and formal operads Duke Math. J. 129(2005), no. 2, 291–335.Google Scholar
[GZ] Gabriel, P. and Zisman, M., Calculus of fractions and homotopy theory. Ergebnisse der Mathematik und Ihrer Grenzgebiete 35, Springer-Verlag, New York, 1967.Google Scholar
[K1] Kleisli, H., Resolutions in additive and non-additive categories . Queen's Papers in Pure and Applied Mathematics 32. Queen's University, Kingston, ON, 1973.Google Scholar
[K2] Kleisli, H., On the construction of standard complexes. J. Pure Appl. Algebra 4(1974), 243–260.Google Scholar
[KS] Kelly, G. M. and Street, R., Review of elements of 2-categories . In: Category Seminar. Lecture Notes in Math. 420, Springer, Berlin, 1974, pp. 75–103.Google Scholar
[Ko] Kontsevich, M., Operads and motives in deformation quantization Lett. Math. Physics 48(1999), no. 1, 35–72.Google Scholar
[ML] Mac Lane, S., Categories for the working mathematician . Graduate Text in Mathematics 5, Springer-Verlag, New York, 1971.Google Scholar
[Maj] Majewski, M., Rational homotopical models and uniqueness. Mem Amer. Math. Soc. 143(2000), no. 682. Society, 2000.Google Scholar
[Man] Mandell, M. A., Cochain multiplications Amer. J. Math. 124(2002), no. 3, 547–566.Google Scholar
[MSS] Markl, M., Shnider, S., and Stasheff, J., Operads in Algebra, Topology and Physics . Mathematical Surveys and Monographs 96, American Mathematical Society, Providence, RI, 2002.Google Scholar
[Mas] Massey, W., Singular Homology Theory . Graduate Texts in Mathematics 70, Springer-Verlag, New York, 1980.Google Scholar
[Mu] Munkholm, H. J., Shm maps of differential graded algebras. J. Pure Appl. Algebra 9, (1976/77), 39–46.Google Scholar
[S] Swan, R. G., Thom's theory of differential forms on simplicial sets Topology 14(1975), no. 3, 271–273.Google Scholar
[T] Tamarkin, D., Formality of chain operad of little discs. Lett. Math. Physics 66(2003), no. 1-2, 65–72.Google Scholar