Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-28T12:48:39.579Z Has data issue: false hasContentIssue false
  • English
  • Français

Morse Index of Approximating Periodic Solutions for the Billiard Problem. Application to Existence Results

Published online by Cambridge University Press:  20 November 2018

Philippe Bolle
Philippe Bolle*
Affiliation:
CEREMADE Université Paris-Dauphine Place du Maréchal de Lattre de Tassigny 75775 Paris cedex 16 France
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper deals with periodic solutions for the billiard problem in a bounded open set of 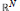${{\mathbb{R}}^{N}}$ which are limits of regular solutions of Lagrangian systems with a potential well. We give a precise link between the Morse index of approximate solutions (regarded as critical points of Lagrangian functionals) and the properties of the bounce trajectory to which they converge.

Keywords

34C2558E50
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 50 , Issue 3 , 01 June 1998 , pp. 497 - 524
Copyright
Copyright © Canadian Mathematical Society 1998

References

1. Babenko, I., Periodic trajectories in three dimensional Birkhoff billiards. Math. URSS Sbornik 71(1992), 1–13.Google Scholar
2. Benci, V., Normal modes of a Lagrangian system constrained in a potential well. Ann. Inst. H. Poincaré Anal. Non Linéaire 1(1984), 379–400.Google Scholar
3. Benci, V. and Giannoni, F., Periodic bounce trajectories with a low number of bounce points. Ann. Inst. H. Poincaré Anal. Non Linéaire (1) 6(1989), 73–93.Google Scholar
4. Birkhoff, G.D., Dynamical systems. Amer. Math. Soc. Colloq. Publ. 9, Amer. Math. Soc., Providence, RI, 1927.Google Scholar
5. Bos, W., Kritische Sehnen auf Riemannschen Elementarraumstücke. Math. Ann. 151(1963), 431–451.Google Scholar
6. Giannoni, F., Periodic bouncing solutions of dynamical conservative systems and their minimal periods. Nonlinear Anal. (3) 14(1990), 263–285.Google Scholar
7. Gluck, H. and Ziller, W., Existence of periodic motions of conservative systems. Ann. of Math. Stud. 103, Princeton University Press, Princeton, NJ, 1983.Google Scholar
8. Kozlov, V. and Treshchëv, D., Billiards. A Genetic introduction to the Dynamics of Systems with Impacts. Transl. Math. Monographs 98, Amer. Math. Soc., Providence, RI, 1991.Google Scholar
9. Ekeland, I. and Hofer, H., Convex Hamiltonian energy surfaces and their periodic trajectories. Comm. Math. Phys. 113(1987), 419–469.Google Scholar
10. Fadell, E.R. and Rabinowitz, P.H., Generalized cohomological index theories for Lie group actions with an application to bifurcation questions for Hamiltonian systems. Invent. Math. 45(1978), 139–174.Google Scholar
11. Marino, A. and Prodi, G., Metodi perturbativi nella teoria di Morse. Boll. Un. Math. Ital. (4) 11, Suppl. fasc. 3 (1975), 1–32.Google Scholar
12. Viterbo, C., Indice de Morse des points critiques obtenus par minimax. Ann. Inst. H. Poincaré Anal.Non Linéaire (3) 5(1988), 221–225.Google Scholar