Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-10T19:45:31.802Z Has data issue: false hasContentIssue false
  • English
  • Français

Moving Ergodic Theorems for Superadditive Processes

Published online by Cambridge University Press:  20 November 2018

S. E. Ferrando
S. E. Ferrando*
Affiliation:
Department of Mathematics, University of Toronto, Toronto, Ontario, M5S1A1 e-mail: ferrando@math. toronto. edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

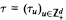Let be a semigroup of measure preserving transformations on a measure space (Ω, ℱ, μ). The main result of the paper is the proof of a.e. convergence for the moving averages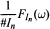 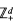where {FIn} is a superadditive process and {In} is a sequence of cubes in satisfying the "cone-condition". The identification of the limit is given. A moving local theorem is also proved.

Keywords

28D9947A35
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 47 , Issue 4 , 01 August 1995 , pp. 728 - 743
Copyright
Copyright © Canadian Mathematical Society 1995

References

1. Akcoglu, M.A. and Déniel, Y., Moving weighted averages, Canad. J. Math. 45(1993), 440–469.Google Scholar
2. Akcoglu, M.A. and Krengel, U., Ergodic theorems for superadditive processes, J. Reine Angew. Math. 323(1981), 53–67.Google Scholar
3. Akcoglu, M.A. and Sucheston, L., A ratio ergodic theorem for superadditive processes, Z.Wahrscheinlichkeitstheorie Verv. Gelbiete 44(1978), 269–278.Google Scholar
4. Below, A., Jones, R. and Rosenblatt, J., Convergence for moving averages, Ergodic Theory Dynamical Systems 10(1990), 43–62.Google Scholar
5. Jones, R.L. and Olsen, J., Multi-parameter moving averages, Almost Every Convergence II, Proceedings of the International Conference on Almost Everywhere Convergence in Probability and Ergodic Theory, Evanston, Illinois, (eds. Below, A. and Jones, R.), 127–148. 1992.Google Scholar
6. Krengel, U., Ergodic Theorems, Stud. Math., (1985).Google Scholar
7. Nagel, A. and Stein, E.M., On certain maximal functions and approach regions, Adv. in Math. 54(1984), 83–106.Google Scholar
8. Rosenblatt, J. and Weirdl, M., A new maximal inequality and its applications, Ergodic Theory Dynamical Systems 12(1992), 509–558.Google Scholar
9. Sueiro, J., A note on maximal operators of Hardy-Littlewood type, Math. Proc. Cambridge Philos. Soc. 102(1987), 131–134.Google Scholar
10. Wittmann, R., On a maximal inequality of Rosenblatt and Wierdl, preprint.Google Scholar