Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-28T02:22:47.270Z Has data issue: false hasContentIssue false
  • English
  • Français

Multiparameter Variational Eigenvalue Problems With Indefinite Nonlinearity

Published online by Cambridge University Press:  20 November 2018

Tetsutaro Shibata
Tetsutaro Shibata*
Affiliation:
The Division of Mathematical and Information Sciences, Faculty of Integrated Arts and Sciences, Hiroshima University, Higashi-Hiroshima, 739 Japan
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We consider the multiparameter nonlinear Sturm-Liouville problem

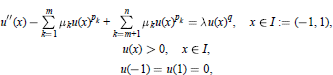
where 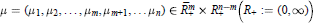are parameters. We assume that

1 ≤ q ≤ p1 < p2 < ... ≤ pn < 2q + 3.

We shall establish an asymptotic formula of variational eigenvalue λ = λ(μ, α) obtained by using Ljusternik-Schnirelman theory on general level set Nμ, α(α < 0 : parameter of level set). Furthermore,we shall give the optimal condition of {(μ, α)}, under which μi(m + 1 ≤ i ≤ n : fixed) dominates the asymptotic behavior of λ(μ, α).

Keywords

34B1534B25
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 49 , Issue 5 , 01 October 1997 , pp. 1066 - 1088
Copyright
Copyright © Canadian Mathematical Society 1997

References

1. Berestycki, H. and Lions, P.L., Nonlinear scalar field equations, I, Existence of a ground state, Arch. Rational Mech. Analysis 82(1983), 313–345.Google Scholar
2. Faierman, M., Two-parameter eigenvalue problems in ordinary differential equations, Longman House, Essex, UK.Google Scholar
3. Gidas, B.,Ni, W.M. and L.Nirenberg, Symmetry and related properties via the maximum principle, Commn. Math. Phys. 68(1979), 209–243.Google Scholar
4. Shibata, T., Asymptotic behavior of eigenvalues of two-parameter nonlinear Sturm-Liouville problems, J. Analyse Math. 66(1995), 277–294.Google Scholar
5. Shibata, T., Variational eigencurve and bifurcation for two-parameter nonlinear Sturm-Liouville equations, Topol. Methods Nonlinear Anal. 8(1996. 79–93.Google Scholar
6. Turyn, L., Sturm-Liouville problems with several parameters, J. Differential Equations 38(1980), 239–259.Google Scholar
7. Zeidler, E., Ljusternik-Schnirelman theory on general level sets, Math. Nachr. 129(1986), 235–259.Google Scholar