Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T14:53:13.740Z Has data issue: false hasContentIssue false
  • English
  • Français

Multiplication Formulas and Canonical Bases for Quantum Affine gln

Published online by Cambridge University Press:  20 November 2018

Jie Du  and
Zhonghua Zhao
Jie Du
Affiliation:
School of Mathematics and Statistics, University of New South Wales, Sydney 2052, Australia email: j.du@unsw.edu.au
Zhonghua Zhao
Affiliation:
Department of Mathematics, Beijing University of Chemical Technology, Beijing 100029, China email: zhaozh@mail.buct.edu.cn
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We will give a representation-theoretic proof for the multiplication formula in the Ringel-Hall algebra $\mathfrak{H}\vartriangle \,(n)$ of a cyclic quiver $\Delta \,(n)$. As a first application, we see immediately the existence of Hall polynomials for cyclic quivers, a fact established by J. Y. Guo and C. M. Ringel, and derive a recursive formula to compute them. We will further use the formula and the construction of a monomial basis for $\mathfrak{H}\vartriangle \,(n)$ given by Deng, Du, and Xiao together with the double Ringel-Hall algebra realisation of the quantum loop algebra 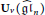${{U}_{v}}({{\widehat{\mathfrak{g}\mathfrak{l}}}_{n}})$ given by Deng, Du, and Fu to develop some algorithms and to compute the canonical basis for 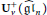$U_{v}^{+}({{\widehat{\mathfrak{g}\mathfrak{l}}}_{n}})$. As examples, we will show explicitly the part of the canonical basis associated with modules of Lowey length at most 2 for the quantum group ${{U}_{v}}({{\widehat{\mathfrak{g}\mathfrak{l}}}_{2}})$.

Keywords

16G2020G42Ringel-Hall algebraquantum groupcyclic quivermonomial basiscanonical basis
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 70 , Issue 4 , 01 August 2018 , pp. 773 - 803
Copyright
Copyright © Canadian Mathematical Society 2018

References

[1] Beilinson, A. A., Lusztig, G., and MacPherson, R., A geometric setting for the quantum deformation of GLn . Duke Math. J. 61(1990), no. 2, 655–677. http://dx.doi.org/10.1215/S0012-7094-90-06124-1 Google Scholar
[2] Bongartz, K., On degenerations and extensions of finite dimensional modules. Adv. Math. 121(1996), 245–287. http://dx.doi.Org/10.1006/aima.1996.0053 Google Scholar
[3] Deng, B. and Du, J., Monomial bases for quantum affine . Adv. Math. 191(2005), 276–304. http://dx.doi.Org/10.1016/j.aim.2004.03.008 Google Scholar
[4] Deng, B., Du, J., and Fu, Q., A double Hall algebra approach to affine quantum Schur-Weyl theory. London Mathematical Society Lecture Note Series, 401, Cambridge University Press, Cambridge, 2012. http://dx.doi.Org/10.1017/CBO9781139226660 Google Scholar
[5] Deng, B., Du, J., Parashall, B., and Wang, J., Finite dimensional algebras and quantum groups. Mathematical Surveys and Monographs, 150, American Mathematical Society, Providence, RI, 2008. http://dx.doi.Org/10.1090/surv/150 Google Scholar
[6] Deng, B., Du, J., and Xiao, J., Generic extensions and canonical bases for cyclic quivers. Canad. J. Math. 59(2007), no. 6, 1260–1283. http://dx.doi.Org/10.4153/CJM-2007-054-7 Google Scholar
[7] Drinfeld, V., A new realization ofYangians and quantized affine algebras. Sov. Math. Dokl. 36(1988), no. 2, 212–216.Google Scholar
[8] Du, J., IC bases and quantum linear groups. Proc. Sympos. Pure Math. 56(1994), 135–148.Google Scholar
[9] Du, J. and Fu, Q., A modified BLM approach to quantum affine . Math. Z. 266(2010), no. 4, 747–781. http://dx.doi.org/10.1007/s00209-009-0596-6 Google Scholar
[10] Du, J. and Fu, Q., Quantum affine via Hecke algebras. Adv. Math. 282(2015), 23–46. http://dx.doi.Org/10.1016/j.aim.2015.06.007 Google Scholar
[11] Du, J. and Fu, Q., The Integral Quantum loop algebra of . arxiv:1404.5679Google Scholar
[12] Guo, J. Y., The Hall polynomials of a cyclic serial algebra. Comm. Algebra. 23(1995), 743–751. http://dx.doi.org/10.1080/00927879508825245 Google Scholar
[13] Fan, Z., Lai, C., Li, Y., Luo, L., and Wang, W.. Affine flag varieties and quantum symmetric pairs. Memoirs of the AMS, to appear. arxiv:1602.04383Google Scholar
[14] Fan, Z. and Li, Y., Positivity of canonical bases under comultiplication. arxiv:1511.02434v3Google Scholar
[15] Ginzburg, V. and Vasserot, E., Langlands reciprocity for affine quantum groups of type An. Internat. Math. Res. Notices 1993, 67–85. http://dx.doi.Org/10.1155/S1073792893000078 Google Scholar
[16] Jantzen, J. C., Lectures on quantum groups. Graduate Studies in Mathematics, 6, American Mathematical Society, Providence, RI, 1995.Google Scholar
[17] Knuth, D. E., Subspaces, subsets, and partitions. J. Combinatorial Theory Ser. A 10(1971), 178–180.Google Scholar
[18] Lai, C. and Luo, L., An elementary construction of monomial bases of quantum affine . arxiv:1506.07263v1Google Scholar
[19] Lusztig, G., Canonical bases arising from quantized enveloping algebras. J. Amer. Math. Soc. 3(1990), no. 2, 447–498. http://dx.doi.org/10.1090/S0894-0347-1990-1035415-6 Google Scholar
[20] Lusztig, G., Affine quivers and canonical bases. Inst. Hautes Études Sci. Publ. Math. 76(1992), 111–163.Google Scholar
[21] Lusztig, G., Introduction to quantum groups. Progress in Mathematics, 110, Birkhauser, Boston, MA, 1993.Google Scholar
[22] Lusztig, G., Tight monomials in quantized enveloping algebras. In: Quantum deformations of algebras and their representations, Israel Math. Conf. Proc., 7, Bar-Ilan University, Ramat Gan, 1993, pp. 117–132.Google Scholar
[23] Lusztig, G., Aperiodicity in quantum affine . Asian J. Math. 3(1999), 147–177. http://dx.doi.org/10.4310/AJM.1999.v3.n1.a7 Google Scholar
[24] Reineke, M., Generic extensions and multiplicative bases of quantum groups at q = 0. Represent. Theory. 5(2001), 147–163. http://dx.doi.Org/10.1090/S1088-4165-01-00111-X Google Scholar
[25] Ringel, C. M., Hall algebras and quantum groups. Invent. Math. 101(1990), 583–592. http://dx.doi.org/10.1007/BF01231516 Google Scholar
[26] Lusztig, G., Hall algebras revisited. In: Quantum deformations of algebras and their representations, Israel Math. Conf. Proc, 7, Bar-Ilan University, Ramat Gan, 1993, pp. 171–176.Google Scholar
[27] Lusztig, G., The composition algebra of a cyclic quiver. Proc. London Math. Soc. 66(1993), 507–537. http://dx.doi.Org/10.1112/plms/s3-66.3.507 Google Scholar
[28] Schiffmann, O., Lectures on Hall algebras. In: Geometric methods in representation theory. II., Sémin. Congr., 24, Soc. Math. France, Paris, 2012, pp. 1–141.Google Scholar
[29] Varagnolo, M. and Vasserot, E., On the decomposition matrices of the quantized Schur algebra. Duke Math. J. 100(1999), 267–297. http://dx.doi.org/10.1215/S0012-7094-99-10010-X Google Scholar
[30] Xi, N., Canonical basis for type A3 . Comm. Algebra. 27(1999), no. 11, 5703–5710. http://dx.doi.org/10.1080/00927879908826784 Google Scholar
[31] Xi, N., Canonical basis for type B2 . J. Algebra. 214(1999), no. 1, 8–21. http://dx.doi.Org/10.1006/jabr.1998.7688 Google Scholar
[32] Xiao, J., Drinfeld double and Ringel-Green theory of Hall algebras. J. Algebra. 190(1997), no. 1, 100–144. http://dx.doi.Org/10.1006/jabr.1996.6887 Google Scholar
[33] Zwara, G., Degenerations for modules over representation-finite biserial algebras. J. Algebra. 198(1997), no. 2, 563–581. http://dx.doi.Org/10.1006/jabr.1997.7160 Google Scholar