Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-28T01:49:11.341Z Has data issue: false hasContentIssue false
  • English
  • Français

Multiplicity Results for Nonlinear Neumann Problems

Published online by Cambridge University Press:  20 November 2018

Michael Filippakis ,
Leszek Gasiński  and
Nikolaos S. Papageorgiou
Michael Filippakis
Affiliation:
Department of Mathematics, National Technical University, Zografou Campus, Athens 15780, Greece
Leszek Gasiński
Affiliation:
Jagiellonian University, Institute of Computer Science, ul. Nawojki 11, 30072 Cracow, Poland email: gasinski@softlab.ii.uj.edu.pl
Nikolaos S. Papageorgiou
Affiliation:
Department of Mathematics, National Technical University, Zografou Campus, Athens 15780, Greece email:npapg@math.ntua.gr
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we study nonlinear elliptic problems of Neumann type driven by the 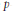$p$-Laplacian differential operator. We look for situations guaranteeing the existence of multiple solutions. First we study problems which are strongly resonant at infinity at the first (zero) eigenvalue. We prove five multiplicity results, four for problems with nonsmooth potential and one for problems with a 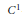${{C}^{1}}$-potential. In the last part, for nonsmooth problems in which the potential eventually exhibits a strict super-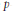$p$-growth under a symmetry condition, we prove the existence of infinitely many pairs of nontrivial solutions. Our approach is variational based on the critical point theory for nonsmooth functionals. Also we present some results concerning the first two elements of the spectrum of the negative 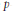$p$-Laplacian with Neumann boundary condition.

Keywords

35J2035J6035J85Nonsmooth critical point theorylocally Lipschitz functionClarke subdifferentialNeumann problemstrong resonancesecond deformation theoremnonsmooth symmetric mountain pass theoremp-Laplacian.
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 58 , Issue 1 , 01 February 2006 , pp. 64 - 92
Copyright
Copyright © Canadian Mathematical Society 2006

References

[1] Anane, A., Etude des Valeurs Propres et de la Resonance pour l’Operateur p-Laplacian. Thése de Doctorat, Univesite Libre de Bruxelles, Faculte des Sciences, 1987.Google Scholar
[2] Bartolo, P., Benci, V. and Fortunato, D., Abstract Critical Point Theorems and Applications to some Nonlinear Problems with “Strong” Resonance at Infinity. Nonlinear Anal. 7(1983), 981–1012.Google Scholar
[3] Binding, P., Drabek, P. and Huang, Y. X., Existence of Multiple Solutions of Critical Quasilinear Elliptic Neumann Problems. Nonlinear Anal. 42(2000), 613–629.Google Scholar
[4] Casas, E. and Fernandez, L. A., A Green's Formula for Quasilinear Elliptic Operators. J. Math. Anal. Appl. 142(1989), 62–73.Google Scholar
[5] Chang, K. C., Variational Methods for Nondifferentiable Functionals and their Applications to Partial Differential Equations. J. Math. Anal. Appl. 80(1981), 102–129.Google Scholar
[6] Chang, K. C., Infinite Dimensional Morse Theory and Multiple Solutions Problems. Birkhäuser, Boston, 1993.Google Scholar
[7] Clarke, F. H., Optimization and Nonsmooth Analysis, Willey, New York, 1983.Google Scholar
[8] Denkowski, Z., Migórski, S. and Papageorgiou, N. S., An Introduction to Nonlinear Analysis: Theory. Kluwer/Plenum, New York, 2003.Google Scholar
[9] Denkowski, Z., Migórski, S. and Papageorgiou, N. S., An Introduction to Nonlinear Analysis: Applications. Kluwer/Plenum, New York, 2003.Google Scholar
[10] Faraci, F., Multiplicity results for a Neumann Problem Involving the p-Laplacian. J. Math. Anal. Appl. 277(2003), 180–189.Google Scholar
[11] Harris, G. A., On Multiple Solutions of a Nonlinear Neumann Problem. J. Differential Equations 95(1992), 105–129.Google Scholar
[12] Hart, D. C., Lazer, A. C. and McKenna, P. J., Multiplicity of Solutions of Nonlinear Boundary Value Problems. SIAMJ. Math. Anal. 17(1986), 1332–1338.Google Scholar
[13] Hu, S. and Papageorgiou, N. S., Handbook of Multivalued Analysis. Volume II: Applications. Kluwer, Dordrecht, The Netherlands, 2000.Google Scholar
[14] John, O., Kufner, A. and Fučik, S., Functional Spaces. Noordhoff International Publishing, Leyden, The Netherlands, 1977.Google Scholar
[15] Kenmochi, N., Pseudomonotone Operators and Nonlinear Elliptic Boundary Value Problems. J. Math. Soc. Japan 27(1975), 121–149.Google Scholar
[16] Kourogenis, N. and Papageorgiou, N. S., Nonsmooth Critical Point Theory and Nonlinear Elliptic Equations at Resonance. J. Austral. Math. Soc. Ser. A 69(2000), 245–271.Google Scholar
[17] Struwe, M., Variational Methods. Springer-Verlag, Berlin, 1990.Google Scholar
[18] Szulkin, A., Minimax Principles for Lower Semicontinuous Functions and Applications to Nonlinear Boundary Value Problems. Ann. Inst. H. Poincaré. Anal. Non Linéaire 3(1986), 77–109.Google Scholar