Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-13T10:33:00.606Z Has data issue: false hasContentIssue false
  • English
  • Français

Navier Stokes Derivative Estimates in Three Dimensions with Boundary Values and Body Forces

Published online by Cambridge University Press:  20 November 2018

G. F. D. Duff
G. F. D. Duff*
Affiliation:
Department of Mathematics, University of Toronto, Toronto, Ontario M5S 1A1
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For a vector solution u(x, t) with finite energy of the Navier Stokes equations with body forces and boundary values on a region Ω ⊆ R3 for t > 0, conditions are established on the L6/5(Ω) and L2(Ω) norms of derivatives of the data that ensure the estimates 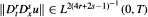and max 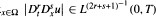, up to any given integer value of the weighted order 2r+s, where r or s = s1 + s2 + s3 > 0 and 0 < T < ∞.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 43 , Issue 6 , 01 December 1991 , pp. 1161 - 1212
Copyright
Copyright © Canadian Mathematical Society 1991

References

1. Adams, R.A. and Fournier, J.J., Cone conditions and properties of Sobolev spaces, J. Math. Anal. App. 61(1977), 713–734.Google Scholar
2. Caffarelli, L., Kohn, R. and Nirenberg, L., Partial regularity of suitable weak solutions of the Navier Stokes equations, Comm. Pure Appl. Math. 35(1982), 771–831.Google Scholar
3. Duff, G.F.D., Navier Stokes derivative estimates in three space dimensions with boundary values and body forces, Math C.R. Reports Acad. Sci. Canada 11(1989), 195–200.Google Scholar
4. Duff, G.F.D., Derivative estimates for the Navier Stokes equations in a three dimensional region, Acta. Math. 164(1990), 145–210.Google Scholar
5. Foias, C., Guillopé, C. and Temam, R., New a priori estimates for the Navier Stokes equations in dimension 3, Comm. Partial Differential Equations 6(1981), 329–359.Google Scholar
6. Heywood, J., The Navier Stokes equations—On the existence, regularity and decay of solutions, Indiana Univ. Math. J. 29(1980), 639–681.Google Scholar
7. Hardy, G.H., Littlewood, J.E. and Polya, G., Inequalities. Cambridge U.P., 1934, xii + 324 pp.Google Scholar
8. Khinchin, A., A course of mathematical analysis. Hindustan Pub. Delhi, 1960, xii + 668 pp.Google Scholar
9. Ladyzhenskaya, O.A., The mathematical theory of viscous incompressible flow. Gordon and Breach, New York, 2nd edition, 1969, xviii + 244 pp.Google Scholar
10. Leray, J., Sur le mouvement d'un liquide visqueux emplissant l'espace, Acta Math. 63(1934), 193–248.Google Scholar
11. McShane, E.J., Unified Integration, Academic Press, New York, 1983, xiii + 607 pp.Google Scholar
12. Scheffer, V., The Navier Stokes equations on a bounded domain, Comm. Math. Phys. 73(1980), 1–42.Google Scholar
13. Serrin, J.B., The initial value problem for the Navier Stokes equations, Nonlinear Problems, Univ. of Wisconsin Press, Madison, 1963,69–98.Google Scholar
14. Wheeden, R.L. and Zygmund, A., Measure and integral, An Introduction to Real Analysis. Dekker, New York, 1977.Google Scholar