Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-10T11:45:32.272Z Has data issue: false hasContentIssue false
  • English
  • Français

Necessary and Sufficient Conditions for Mean Convergence of Lagrange Interpolation for Erdős Weights

Published online by Cambridge University Press:  20 November 2018

S. B. Damelin  and
D. S. Lubinsky
S. B. Damelin
Affiliation:
Department of Mathematics University of the Witwatersrand P.O. Wits 2050 Republic of South Africa
D. S. Lubinsky
Affiliation:
Department of Mathematics University of the Witwatersrand P.O. Wits 2050 Republic of South Africa
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We investigate mean convergence of Lagrange interpolation at the zeros of orthogonal polynomials pn(W2, x) for Erdös weights W2 = e-2Q. The archetypal example is Wk,α = exp(—Qk,α), where

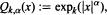
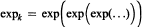α > 1, k ≥ 1, and is the k-th iterated exponential. Following is our main result: Let 1 < p < ∞, Δ ∊ ℝ, k > 0. Let Ln[f] denote the Lagrange interpolation polynomial to ƒ at the zeros of pn(W2, x) = pn(e-2Q, x). Then for

to hold for every continuous function ƒ: ℝ —> ℝ satisfying

it is necessary and sufficient that

Keywords

42C1542C0565D05Erdős weightsLagrange interpolationmean convergenceLp norms
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 48 , Issue 4 , 01 August 1996 , pp. 710 - 736
Copyright
Copyright © Canadian Mathematical Society 1996

References

1. Bonan, S.S., Weighted mean convergence of Lagrange interpolation, Ph. D. Thesis, Ohio State University, Columbus, Ohio, 1982.Google Scholar
2. Clunie, J., Kovari, T., On integral functions having prescribed asymptotic growth II, Canad. J., Math. 20(1968), 7–20.Google Scholar
3. Freud, G., Orthogonal polynomials, Pergamon Press/Akademiai Kiado, Budapest, 1970.Google Scholar
4. Knopfmacher, A. and Lubinsky, D.S., Mean convergence of Lagrange interpolation for Freud's weights with application to product integration rules, J. Comp. Appl., Math. 17(1987), 79–103.Google Scholar
5. Koosis, P., The Logarithmic Integral I, Cambridge University Press, Cambridge, 1988.Google Scholar
6. Levin, A.L. and Lubinsky, D.S., Christoffel functions, orthogonal polynomials, and Nevai's conjecture for Freud weights, Constr., Approx. 8(1992), 463–535.Google Scholar
7. Levin, A.L., Lubinsky, D.S., and Mthembu, T.Z., Christojfel functions and orthogonal polynomials for Erdos weights on (—∞, ∞), Rendiconti di Matematica di, Roma, 14(1994), 199–289.Google Scholar
8. Lubinsky, D.S., An update on orthogonal polynomials and weighted approximation on the real line, Acta Appl., Math. 33(1993), 121–164.Google Scholar
9. Lubinsky, D.S., An extension of the Erdos--Turan inequality for the sum of successive fundamental polynomials, Ann. Numer., Math. 2(1995), 305–309.Google Scholar
10. Lubinsky, D.S., The weighted Lp norms of orthonormal polynomials for Erdos weights, Comput. Math. Appl., to appear.Google Scholar
11. Lubinsky, D.S. and Matjila, D.M., Necessary and sufficient conditions for mean convergence of Lagrange interpolation for Freud weights, SIAM J. Math., Anal. 26(1995), 238–262.Google Scholar
12. Lubinsky, D.S. and Mthembu, T.Z., Lp Markov—Bernstein inequalities for Erdos weights, J. Approx., Theory 65(1991), 301–321.Google Scholar
13. Lubinsky, D.S., Mean convergence of Lagrange interpolation for Erdos weights, J. Comp. Appl., Math. 47(1993), 369–390.Google Scholar
14. Mhaskar, H.N. and Saff, E.B., Where does the sup-norm of a weighted polynomial live?, Constr., Approx. 1(1985), 71–91.Google Scholar
15. Mhaskar, H.N., Where does the Lp-norm of a weighted polynomial live?, Trans. Amer. Math., Soc. 303(1987), 109–124.Google Scholar
16. Nevai, P., Orthogonal Polynomials, Memoirs of the Amer. Math., Soc. 213(1979).Google Scholar
17. Nevai, P., Mean convergence of Lagrange interpolation II, J. Approx., Theory 30(1980), 263–276.Google Scholar
18. Nevai, P., Geza Freud: orthogonal polynomials and Christoff el functions, A Case Study, J. Approx., Theory 48(1986), 3–167.Google Scholar
19. Nevai, P. and Vertesi, P., Mean convergence ofHermite—Fejer interpolation, J. Math. Anal., Appl. 105(1985), 26–58.Google Scholar
20. Stein, E.M., Harmonic analysis: real variable methods, orthogonality and oscillatory integrals, Princeton University Press, Princeton, 1993.Google Scholar
21. Szabados, J. and Vertesi, P., Interpolation of Functions, World Scientific, Singapore, 1991.Google Scholar