Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-27T08:35:24.492Z Has data issue: false hasContentIssue false
  • English
  • Français

A New Result on Comma-Free Codes of Even Word-Length

Published online by Cambridge University Press:  20 November 2018

Betty Tang ,
Solomon W. Golomb  and
Ronald L. Graham
Betty Tang
Affiliation:
University of Southern California, Los Angeles, California
Solomon W. Golomb
Affiliation:
University of Southern California, Los Angeles, California
Ronald L. Graham
Affiliation:
AT&T Bell Laboratories, Murray Hill, New Jersey
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Comma-free codes were first introduced in [1] in 1957 as a possible genetic coding scheme for protein synthesis. The general mathematical setting of such codes was presented in [3], and the biochemical and mathematical aspects of the problem were later summarized and extended in [4].

Using the notation of [3], a set D of k-tuples or k-letter words, (a1a2 … ak), where

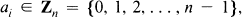
for fixed positive integers k and n, is said to be a comma-free dictionary if and only if, whenever (a1a2 … ak) and (b1b2 … bk) are in D, the “overlaps”

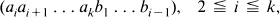
are not in D. This precludes codewords having a subperiod less than k; and two codewords which are cyclic permutations of one another cannot both be in D.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 39 , Issue 3 , 01 June 1987 , pp. 513 - 526
Copyright
Copyright © Canadian Mathematical Society 1987

References

1. Crick, F. H. C., Griffith, J. S. and Orgel, L. E., Codes without commas, Proc. Nat. Acad. Sci. 43 (1957), 416–421.Google Scholar
2. Eastman, W. L., On the construction of comma-free codes, IEEE Trans, on Information Theory, IT-11 (1965), 263–266.Google Scholar
3. Golomb, S. W., Gordon, B. and Welch, L. R., Comma-free codes, Can. J. Math. 10 (1958), 202–209.Google Scholar
4. Golomb, S. W., Welch, L. R. and Delbrück, M., Construction and properties of comma-free codes, Biol. Medd. Dan. Vid. Selsk. 23 (1958), 3–34.Google Scholar
5. Jiggs, B. H., Recent results in comma-free codes, Can. J. Math. 75 (1963), 178–187.Google Scholar
6. Scholtz, R. A., Maximal and variable word-length comma-free codes, IEEE Trans, on Information Theory, IT-15 (1969), 300–306.Google Scholar
7. van Lint, J. H., {0, 1, *} distance problems in combinatorics, Surveys in Combinatorics (1985), London Mathematical Society Lecture Note Series 103 (Cambridge University Press, 1985), 113–135.Google Scholar