Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-11T00:14:01.929Z Has data issue: false hasContentIssue false
  • English
  • Français

Newforms of Half-integral Weight: The Minus Space Counterpart

Part of: Discontinuous groups and automorphic forms

Published online by Cambridge University Press:  31 October 2019

Ehud Moshe Baruch  and
Soma Purkait
Ehud Moshe Baruch
Affiliation:
Department of Mathematics, Technion, Haifa, 32000, Israel Email: embaruch@math.technion.ac.il
Soma Purkait
Affiliation:
Department of Mathematics, Tokyo Institute of Technology, Japan Email: somapurkait@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

We study genuine local Hecke algebras of the Iwahori type of the double cover of 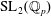$\operatorname{SL}_{2}(\mathbb{Q}_{p})$ and translate the generators and relations to classical operators on the space 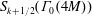$S_{k+1/2}(\unicode[STIX]{x1D6E4}_{0}(4M))$, 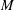$M$ odd and square-free. In [9] Manickam, Ramakrishnan, and Vasudevan defined the new space of 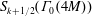$S_{k+1/2}(\unicode[STIX]{x1D6E4}_{0}(4M))$ that maps Hecke isomorphically onto the space of newforms of 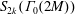$S_{2k}(\unicode[STIX]{x1D6E4}_{0}(2M))$. We characterize this newspace as a common 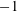$-1$-eigenspace of a certain pair of conjugate operators that come from local Hecke algebras. We use the classical Hecke operators and relations that we obtain to give a new proof of the results in [9] and to prove our characterization result.

Keywords

Hecke algebrahalf-integral weight formNiwa isomorphismKohnen plus space

MSC classification

Primary: 11F37: Forms of half-integer weight; nonholomorphic modular forms
Secondary: 11F12: Automorphic forms, one variable 11F70: Representation-theoretic methods; automorphic representations over local and global fields
Type
Article
Information
Canadian Journal of Mathematics , Volume 72 , Issue 2 , April 2020 , pp. 326 - 372
Copyright
© Canadian Mathematical Society 2019

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Atkin, A. O. L. and Lehner, J., Hecke operators on 𝛤0(m). Math. Ann. 185(1970), 134–160. https://doi.org/10.1007/BF01359701Google Scholar
Baruch, E. M. and Purkait, S., Hecke algebras, new vectors and newforms on 𝛤0(m). Math. Zeit. 287(2017), 705–733. https://doi.org/10.1007/s00209-017-1842-yGoogle Scholar
Baruch, E. M. and Purkait, S., Newforms of half-integral weight: the minus space of S k+1/2(𝛤0(8M)). Israel J. Math. 232(2019), 41–73. https://doi.org/10.1007/s11856-019-1873-7Google Scholar
Gelbart, S., Weil’s representation and the spectrum of the metaplectic group. Lecture Notes in Mathematics, 530, Springer-Verlag, Berlin, 1976.Google Scholar
Kohnen, W., Modular forms of half-integral weight on 𝛤0(4). Math. Ann. 248(1980), 249–266. https://doi.org/10.1007/BF01420529Google Scholar
Kohnen, W., Newforms of half-integral weight. J. Reine Angew. Math. 333(1982), 32–72. https://doi.org/10.1515/crll.1982.333.32Google Scholar
Kumar, N. and Purkait, S., A note on the Fourier coefficients of half-integral weight modular forms. Arch. Math. (Basel) 102(2014), no. 4, 369–378. https://doi.org/10.1007/s00013-014-0622-8Google Scholar
Loke, H. Y. and Savin, G., Representations of the two-fold central extension of [[()[]mml:mo lspace="1em" rspace="0em"[]()]]SL[[()[]/mml:mo[]()]]2(ℚ2). Pacific J. Math. 247(2010), 435–454. https://doi.org/10.2140/pjm.2010.247.435Google Scholar
Manickam, M., Ramakrishnan, B., and Vasudevan, T., On the theory of newforms of half-integral weight. J. Number Theory 34(1990), 210–224. https://doi.org/10.1016/0022-314X(90)90151-GGoogle Scholar
Niwa, S., On Shimura’s trace formula. Nagoya Math. J. 66(1977), 183–202.Google Scholar
Purkait, S., On Shimura’s decomposition. Int. J. Number Theory 9(2013), 1431–1445. https://doi.org/10.1142/S179304211350036XGoogle Scholar
Purkait, S., Hecke operators in half-integral weight. J. Théor. Nombres Bordeaux 26(2014), 233–251.Google Scholar
Savin, G., On unramified representations of covering groups. J. Reine Angew. Math. 566(2004), 111–134. https://doi.org/10.1515/crll.2004.001Google Scholar
Shimura, G., On modular forms of half integral weight. Ann. of Math. 97(1973), 440–481. https://doi.org/10.2307/1970831Google Scholar
Shimura, G., The critical values of certain zeta functions associated with modular forms of half-integral weight. J. Math. Soc. Japan 33(1981), 649–672. https://doi.org/10.2969/jmsj/03340649Google Scholar
Ueda, M., On twisting operators and newforms of half-integral weight. Nagoya Math J. 131(1993), 135–205. https://doi.org/10.1017/S002776300000458XGoogle Scholar
Ueda, M. and Yamana, S., On newforms for Kohnen plus spaces. Math. Z. 264(2010), 1–13. https://doi.org/10.1007/s00209-008-0449-8Google Scholar
Waldspurger, J.-L., Sur les coefficients de Fourier des formes modulaires de poids demi-entier. J. Math. Pures Appl. (9) 60(1981), 375–484.Google Scholar