Hostname: page-component-7f64f4797f-kjzhn Total loading time: 0 Render date: 2025-11-07T05:00:49.883Z Has data issue: false hasContentIssue false
  • English
  • Français

Nonadjacent Radix-τ Expansions of Integers in Euclidean Imaginary Quadratic Number Fields

Published online by Cambridge University Press:  20 November 2018

Ian F. Blake ,
V. Kumar Murty  and
Guangwu Xu
Ian F. Blake
Affiliation:
Department of Electrical and Computer Engineering, University of Toronto, Toronto, ON, M5S 3G4 e-mail: ifblake@comm.utoronto.ca
V. Kumar Murty
Affiliation:
Department of Mathematics, University of Toronto, Toronto, ON, M5S 3G3 e-mail: murty@math.toronto.edu
Guangwu Xu
Affiliation:
Department of Electrical Engineering and Computer Science, University of Wisconsin-Milwaukee, Milwuakee, WI 53211, U.S.A. e-mail: gxu4uwm@uwm.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In his seminal papers, Koblitz proposed curves for cryptographic use. For fast operations on these curves, these papers also initiated a study of the radix- $\tau $ expansion of integers in the number fields 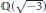$\mathbb{Q}\left( \sqrt{-3} \right)$ and 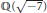$\mathbb{Q}\left( \sqrt{-7} \right)$ . The (window) nonadjacent form of $\tau $ -expansion of integers in 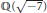$\mathbb{Q}\left( \sqrt{-7} \right)$ was first investigated by Solinas. For integers in 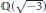$\mathbb{Q}\left( \sqrt{-3} \right)$ , the nonadjacent form and the window nonadjacent form of the $\tau $ -expansion were studied. These are used for efficient point multiplications on Koblitz curves. In this paper, we complete the picture by producing the (window) nonadjacent radix- $\tau $ expansions for integers in all Euclidean imaginary quadratic number fields.

Keywords

Primary: 11A63secondary: 11R0411Y1611Y4014G50algebraic integerradix expressionwindow nonadjacent expansionalgorithmpoint multiplication of elliptic curvescryptography

Information

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 60 , Issue 6 , 01 December 2008 , pp. 1267 - 1282
Copyright
Copyright © Canadian Mathematical Society 2008

References

[1] Blake, I., Seroussi, G., and Smart, N., Elliptic Curves in Cryptography. Cambridge University Press, 1999.Google Scholar
[2] Blake, I., Murty, V. K., and Xu, G., A note on window τ-NAF algorithm. Inform. Process. Lett. 95(2005), no. 5, 496–502.Google Scholar
[3] Blake, I., Murty, V. K., and Xu, G., Efficient algorithms for Koblitz curves over fields of characteristic three. J. Discrete Algorithms 3(2005), no. 1, 113–124.Google Scholar
[4] Boneh, D. and Franklin, M., Identity-based encryption from theWeil pairing. In: Advances in Cryptology–CRYPTO 2001 . Lecture Notes in Computer Science 2139, Springer, Berlin, 2001, pp. 213–239.Google Scholar
[5] Hankerson, D., Menezes, A., and Vanstone, S., Guide to Elliptic Curve Cryptography. Springer-Verlag, New York, 2004.Google Scholar
[6] Koblitz, N., CM-curves with good cryptographic properties.In: Advances in Cryptology–CRYPTO ’91. Lecture Notes in Computer Science 576, Springer, Berlin 1992, pp. 279–287.Google Scholar
[7] Koblitz, N., An elliptic curves implementation of the finite field digital signature algorithm. Advances in Cryptology–CRYPTO ‘98. Lecture Notes in Computer Science 1462, Springer, Berlin, 1998, 327–337.Google Scholar
[8] Koblitz, N., p-adic Numbers, p-adic Analysis, and Zeta-Functions. Second edition. Graduate Texts in Mathematics 58, Springer-Verlag, New York, 1984.Google Scholar
[9] Meier, W. and Staffelbach, O., Efficient multiplication on certain nonsupersingular elliptic curves. Advances in Cryptology–CRYPTO ‘92. Lecture Notes in Computer Science 740, Springer, Berlin, 1993, pp. 333–344.Google Scholar
[10] Muir, J. A. and Stinson, D. R., Minimality and other properties of the width-w nonadjacent form. Math. Comp. 75(2006), no. 253, 369–384.Google Scholar
[11] Müller, V., Fast multiplication on elliptic curves over small fields of characteristic two. J. Cryptology 11(1998), no. 4, 219–234.Google Scholar
[12] Murty, M. R., Introduction to p-Adic Analytic Number Theory. AMS/IP Studies in Advanced Mathematics 27, AmericanMathematical Society, Providence, RI, 2002.Google Scholar
[13] Smart, N., Elliptic curve cryptosystems over small fields of odd characteristic. J. Cryptology 12(1999), no. 2, 141–151.Google Scholar
[14] Solinas, J., Efficient arithmetic on Koblitz curves. Des. Codes Cryptogr. 19(2000), no. 2-3, 195–249.Google Scholar