No CrossRef data available.
Article contents
Noncommutative rational Clark measures
Published online by Cambridge University Press: 27 July 2022
Abstract
We characterize the noncommutative Aleksandrov–Clark measures and the minimal realization formulas of contractive and, in particular, isometric noncommutative rational multipliers of the Fock space. Here, the full Fock space over 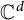 $\mathbb {C} ^d$ is defined as the Hilbert space of square-summable power series in several noncommuting (NC) formal variables, and we interpret this space as the noncommutative and multivariable analogue of the Hardy space of square-summable Taylor series in the complex unit disk. We further obtain analogues of several classical results in Aleksandrov–Clark measure theory for noncommutative and contractive rational multipliers.
$\mathbb {C} ^d$ is defined as the Hilbert space of square-summable power series in several noncommuting (NC) formal variables, and we interpret this space as the noncommutative and multivariable analogue of the Hardy space of square-summable Taylor series in the complex unit disk. We further obtain analogues of several classical results in Aleksandrov–Clark measure theory for noncommutative and contractive rational multipliers.
Noncommutative measures are defined as positive linear functionals on a certain self-adjoint subspace of the Cuntz–Toeplitz algebra, the unital 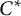 $C^*$-algebra generated by the left creation operators on the full Fock space. Our results demonstrate that there is a fundamental relationship between NC Hardy space theory, representation theory of the Cuntz–Toeplitz and Cuntz algebras, and the emerging field of noncommutative rational functions.
$C^*$-algebra generated by the left creation operators on the full Fock space. Our results demonstrate that there is a fundamental relationship between NC Hardy space theory, representation theory of the Cuntz–Toeplitz and Cuntz algebras, and the emerging field of noncommutative rational functions.
Keywords
MSC classification
- Type
- Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of The Canadian Mathematical Society
Footnotes
The first author was supported by NSF grant DMS-1900364. The second author was supported by NSERC grant 2020-05683.



