Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-13T03:33:12.314Z Has data issue: false hasContentIssue false
  • English
  • Français

Nongaussian Limit Distributions of Lacunary Trigonometric Series

Published online by Cambridge University Press:  20 November 2018

I. Berkes
I. Berkes*
Affiliation:
Mathematical Institute of the Hungarian Academy of Sciences, H-1053 Budapest, Reáltanoda u. 13-15, Hungary
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

It is a well known fact that for rapidly increasing nkthe sequence 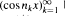, behaves like a sequence of independent random variables; in particular 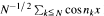has a limiting Gaussian distribution as N → ∞. Under a certain critical speed 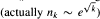this result breaks down and 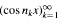becomes strongly dependent. The purpose of this paper is to investigate the asymptotic behavior of normed sums 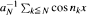in the strongly dependent domain; specifically, we construct a large class of nongaussian limit distributions of such sums.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 43 , Issue 5 , 01 October 1991 , pp. 948 - 959
Copyright
Copyright © Canadian Mathematical Society 1991

References

1. Berkes, I., An almost sure invariance principle for lacunary trigonometric series, Acta Math. Acad. Sci. Hung. 26 (1975), 209–220.Google Scholar
2. Berkes, I., On the central limit theorem for lacunary trigonometric series, Anal. Math 4 (1978), 159–180.Google Scholar
3. Erdős, P., On trigonometric sums with gaps, Magyar Tud. Akad. Mat. Kut. Int. Közl. 7 (1962), 37–42.Google Scholar
4. Erdős, P. and Gál, I. S., On the law of the iterated logarithm, Proc. Nederl. Akad. Wetensch. Ser. A, 58 (1955), 65–84.Google Scholar
5. Gnedenko, B.V. and Kolmogorov, A.N., Limit distributions for sums of independent random variables. Addison-Wesley, Cambridge, 1954.Google Scholar
6. Kac, M., Probability methods in some problems of analysis and number theory, Bull. Amer. Math. Soc. 55 (1949), 641–665.Google Scholar
7. Philipp, W. and Stout, W. F., Almost sure invariance principles for sums of weakly dependent random variables, Memoirs of the AMS, 161 (1975).Google Scholar
8. Ramachandran, B., On characteristic functions and moments, Sankhya A 31 No 1 (1969), 1–12.Google Scholar
9. Salem, R. and Zygmund, A., On lacunary trigonometric series, Proc. Nat. Acad. Sci. USA 33 (1947), 333- 338.Google Scholar
10. Takahashi, S., On the law of the iterated logarithm for lacunary trigonometric series, Tohoku Math. Journ. 24 (1972),319–329.Google Scholar
11. Takahashi, S., On the law of the iterated logarithm for lacunary trigonometric series II, Tohoku Math. Journ. 27 (1975),391–403.Google Scholar
12. Takahashi, S., On lacunary trigonometric series II, Proc. Japan Acad. 44 (1968), 766–770.Google Scholar
13. Takahashi, S., Almost sure invariance principles for lacunary trigonometric series, Tohoku Math. Journ. 31 (1979),439–451.Google Scholar
14. Weiss, M., On the law of the iterated logarithm for lacunary trigonometric series, Trans. Amer. Math. Soc. 91 (1959), 444–469.Google Scholar