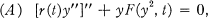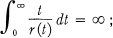Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kitamura, Yuichi
and
Kusano, Takaŝi
1978.
Nonlinear oscillation of a fourth order elliptic equation.
Journal of Differential Equations,
Vol. 30,
Issue. 2,
p.
280.
Naito, Manabu
1978.
On positive solutions of fourth order nonlinear differential inequalities.
Annali di Matematica Pura ed Applicata,
Vol. 117,
Issue. 1,
Grammatikopulos, M. K.
1979.
Influence of deviating arguments on the behavior of the bounded solutions of nonlinear differential equations.
Ukrainian Mathematical Journal,
Vol. 30,
Issue. 4,
p.
357.
Onose, Hiroshi
1979.
Nonlinear oscillation of fourth order functional differential equations.
Annali di Matematica Pura ed Applicata,
Vol. 119,
Issue. 1,
p.
259.
Grammatikopoulos, M. K.
1979.
A criterion for the existence of bounded nonoscillatory solutions for nonlinear retarded differential equatory.
Annali di Matematica Pura ed Applicata,
Vol. 120,
Issue. 1,
p.
25.
Elias, Uri
and
Kreith, Kurt
1980.
Nonlinear differential systems with monotone solutions.
Hiroshima Mathematical Journal,
Vol. 10,
Issue. 3,
Granata, Antonio
1980.
Canonical Factorizations of Disconjugate Differential Operators.
SIAM Journal on Mathematical Analysis,
Vol. 11,
Issue. 1,
p.
160.
Kitamura, Yuichi
1980.
Characterization of oscillation of fourth order functional differential equations with deviating arguments.
Annali di Matematica Pura ed Applicata,
Vol. 124,
Issue. 1,
p.
345.
Kreith, Kurt
1980.
Extremal solutions for a class of nonlinear differential equations.
Proceedings of the American Mathematical Society,
Vol. 79,
Issue. 3,
p.
415.
Edelson, Allan L.
1982.
Nonlinear Phenomena in Mathematical Sciences.
p.
343.
Swanson, C. A.
and
Gilbert, Robert
1983.
Bounded Positive Solutions of Quasilinear Schrödinger Equations.
Applicable Analysis,
Vol. 14,
Issue. 3,
p.
179.
Kreith, K.
and
Swanson, C. A.
1983.
Ordinary Differential Equations and Operators.
Vol. 1032,
Issue. ,
p.
298.
Edelson, Allan L.
and
Schuur, Jerry D.
1986.
Increasing solutions of.
Nonlinear Analysis: Theory, Methods & Applications,
Vol. 10,
Issue. 2,
p.
195.
Iraniparast, N.
1987.
Qualitative behaviour of solutions of the Goursat problem for hyperbolic differential equations.
Computers & Mathematics with Applications,
Vol. 13,
Issue. 9-11,
p.
889.
Edelson, Allan L.
1989.
Entire solutions of singular elliptic equations.
Journal of Mathematical Analysis and Applications,
Vol. 139,
Issue. 2,
p.
523.
Gopalsamy, K.
Wen, Lizhi
Chen, Yong‐Shao
and
He, Xue‐Zhong
1993.
Necessary and Sufficient Conditions for a Fourth Order Functional Differential Equation to be Oscillatory.
Mathematische Nachrichten,
Vol. 164,
Issue. 1,
p.
23.
Zhang, Bing Gen
and
Cheng, Sui Sun
1995.
On a class of nonlinear difference equations.
Journal of Difference Equations and Applications,
Vol. 1,
Issue. 4,
p.
391.
Kamo, K.-I.
and
Usami, H.
2002.
Oscillation theorems for fourth-order quasilinear ordinary differential equations.
Studia Scientiarum Mathematicarum Hungarica,
Vol. 39,
Issue. 3-4,
p.
385.
Takaŝi, Kusano
and
Tanigawa, Tomoyuki
2006.
On the structure of positive solutions of a class of fourth order nonlinear differential equations.
Annali di Matematica Pura ed Applicata,
Vol. 185,
Issue. 4,
p.
521.
Kamo, Ken-ichi
and
Usami, Hiroyuki
2011.
Nonlinear oscillations of fourth order quasilinear ordinary differential equations.
Acta Mathematica Hungarica,
Vol. 132,
Issue. 3,
p.
207.