Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-13T05:42:21.876Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-Orientable Surfaces and Dehn Surgeries

Published online by Cambridge University Press:  20 November 2018

D. Matignon  and
N. Sayari
D. Matignon
Affiliation:
Université d’Aix-Marseille I, C.M.I. 39, rue Joliot Curie, F-13453 Marseille Cedex 13, France e-mail: matignon@cmi.univ-mrs.fr
N. Sayari
Affiliation:
Université de Moncton, Département de Mathematiques et de Statistique, Moncton, New Brunswick, E1A 3E9 e-mail: sayarin@umoncton.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 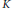$K$ be a knot in 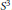${{S}^{3}}$ . This paper is devoted to Dehn surgeries which create 3-manifolds containing a closed non-orientable surface 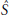$\hat{S}$ . We look at the slope 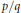$p/q$ of the surgery, the Euler characteristic 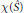$\mathcal{X}(\hat{S})$ of the surface and the intersection number $s$ between 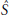$\hat{S}$ and the core of the Dehn surgery. We prove that if 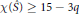$\mathcal{X}(\hat{S})\,\ge \,15\,-3q$, then 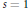$s\,=\,1$. Furthermore, if 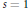$s\,=\,1$ then 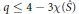$q\,\le \,4\,-\,3\,\mathcal{X}(\hat{S})$ or 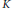$K$ is cabled and 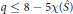$q\,\le \,8\,-5\mathcal{X}(\hat{S})$ . As consequence, if 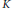$K$ is hyperbolic and 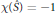$\mathcal{X}(\hat{S})\,=\,-1$ , then 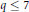$q\,\le \,7$.

Keywords

57M2557N1057M15Non-orientable surfaceDehn surgeryIntersection graphs
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 56 , Issue 5 , 01 October 2004 , pp. 1022 - 1033
Copyright
Copyright © Canadian Mathematical Society 2004

References

[1] Culler, M., Gordon, C. McA., Luecke, J. and Shalen, P. B., Dehn surgery on knots. Ann.Math. 125(1987), 237–300.Google Scholar
[2] Delman, C. and Roberts, R., Alternating knots satisfy strong property P. Comment.Math. Helv. 74(1999), 376–397.Google Scholar
[3] Eudave-Muñoz, M., Non-hyperbolic manifolds obtained by Dehn surgery on hyperbolic knots. Geometric Topology, Athens, GA, 1993, 35–61, Amer. Math. Soc. IP Stud. Adv. Math. 2.1, Amer. Math. Soc., Providence, RI, 1997.Google Scholar
[4] Gabai, D., Foliations and the topology of 3-manifolds, III. J. Differential Geom. 26(1987), 479–536.Google Scholar
[5] Gonzàlez-Acuña, F. and Short, H., Knot surgery and primeness. Math. Proc. Cambridge Philos. Soc. 99(1986), 89–102.Google Scholar
[6] Gordon, C. McA., Boundary slopes of punctured tori in 3-manifolds. Trans. Amer. Math. Soc. 350(1998), 1713–1790.Google Scholar
[7] Gordon, C. McA., Combinatorial methods in Dehn surgery. Series on Knots and Everything 15, World Scientific Publishing, River Edge, NJ, 1997, pp. 263–290.Google Scholar
[8] Gordon, C. McA. and Litherland, R. A., Incompressible planar surfaces in 3-manifolds. Topology Appl. 18(1984), 181–144.Google Scholar
[9] Gordon, C. McA. and Luecke, J., Dehn surgeries on knots creating essential tori, I. Comm. Anal. Geom. 3(1995), 597–644.Google Scholar
[10] Gordon, C. McA. and Luecke, J., Dehn surgeries on knots creating essential tori, II. Comm. Anal. Geom. 8(2000) 671–725.Google Scholar
[11] Gordon, C. McA. and Luecke, J., Non-integral, toroidal Dehn surgeries. preprint.Google Scholar
[12] Gordon, C. McA. and Luecke, J., Only integral surgeries can yield reducible manifolds. Math. Proc. Cambridge Philos. Soc. 102(1987), 97–101.Google Scholar
[13] Gordon, C. McA. and Luecke, J., Reducible manifolds and Dehn surgery. Topology (2) 35(1996), 385–409.Google Scholar
[14] Hayashi, C. and Motegi, K., Only single twists on unknots can produce composite knots. Trans. Amer. Math. Soc. 349(1997), 151–164.Google Scholar
[15] Ichihara, K., Ohtouge, M. and Teragaito, M., Boundary slopes of non-orientable Seifert surfaces for knots. Topology Appl. 122(2002), 467–478.Google Scholar
[16] Matignon, D., P 2 -reducibility of 3-manifolds. Kobe J. Math. 14(1997), 33–47.Google Scholar
[17] Rolfsen, D., Knots and Links. Mathematics Lecture Series 7, Publish or Perish, Berkeley, California, 1976.Google Scholar