Hostname: page-component-7bb8b95d7b-pwrkn Total loading time: 0 Render date: 2024-09-20T12:44:14.805Z Has data issue: false hasContentIssue false
  • English
  • Français

Non-tame Mice from Tame Failures of the Unique Branch Hypothesis

Published online by Cambridge University Press:  20 November 2018

Grigor Sargsyan  and
Nam Trang
Grigor Sargsyan
Affiliation:
Department of Mathematics, Rutgers University, New Brunswick, NJ, 08854 USA. e-mail: grigor@math.rutgers.edu
Nam Trang
Affiliation:
Department of Mathematical Sciences, Carnegie Mellon University, Pittsburgh, PA, 15213 USA. e-mail: namtrang@andrew.cmu.edu
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we show that the failure of the unique branch hypothesis 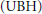$\left( \text{UBH} \right)$ for tame trees implies that in some homogenous generic extension of 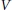$V$ there is a transitive model 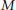$M$ containing Ord 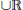$\cup \mathbb{R}$ such that 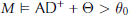$M\,\vDash \,\text{A}{{\text{D}}^{+}}\,+\,\Theta \,>\,{{\theta }_{0}}$. In particular, this implies the existence (in 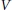$V$) of a non-tame mouse. The results of this paper significantly extend J. R. Steel's earlier results for tame trees.

Keywords

03E1503E4503E60mouseinner model theorydescriptive set theoryhod mousecore model inductionUBH
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 66 , Issue 4 , 01 August 2014 , pp. 903 - 923
Copyright
Copyright © Canadian Mathematical Society 2014

Footnotes

*

The first author's work was supported by NSF Grant No DMS-1201348.

References

[1] Jech, T., Set theory. The third millennium ed., revised and expanded, Springer Monographs in Mathematics, Springer-Verlag, Berlin, 2003.Google Scholar
[2] Ketchersid, R. O., Toward ADℝ from the continuum hypothesis and an ω1-dense ideal. Ph.D. Thesis, University of California, Berkeley, ProQuest LLC, Ann Arbor, MI, 2000.Google Scholar
[3] Martin, D. A. and Steel, J. R., Iteration trees. J. Amer. Math. Soc. 7(1994), no. 1, 1–73. http://dx.doi.org/10.1090/S0894-0347-1994-1224594-7 CrossRefGoogle Scholar
[4] Mitchell, W. J. and Steel, J. R., Fine structure and iteration trees. Lecture Notes in Logic, 3, Springer-Verlag, Berlin, 1994.Google Scholar
[5] Neeman, I., Inner models in the region of a Woodin limit of Woodin cardinals. Ann. Pure Appl. Logic 116(2002), no. 1–3, 67–155. http://dx.doi.org/10.1016/S0168-0072(01)00103-8 CrossRefGoogle Scholar
[6] Sargsyan, G., Descriptive inner model theory. Bull. Symbolic Logic, to appear. http://math.rutgers.edu/_gs481. http://dx.doi.org/10.2178/bsl.1901010 CrossRefGoogle Scholar
[7] Sargsyan, G., On the strength of PFAI. http://math.rutgers.edu/_gs481. Google Scholar
[8] Sargsyan, G., A tale of hybrid mice. http://math.rutgers.edu/_gs481/. Google Scholar
[9] Schindler, R. and Steel, J. R., The core model induction. http://math.berkeley.edu/_steel. Google Scholar
[10] Schlutzenberg, F. and Trang, N., Scales in LpΣ(ℝ). http://math.cmu.edu/_namtrang. Google Scholar
[11] Steel, J. R., PFA implies ADL(ℝ). J. Symbolic Logic 70(2005), no. 4, 1255–1296. http://dx.doi.org/10.2178/jsl/1129642125 CrossRefGoogle Scholar
[12] Steel, J. R., Derived models associated to mice. In: Computational prospects of infinity. Part I. Tutorials, Lect. Notes Ser. Inst.Math. Sci. Natl. Univ. Singap., 14,World Sci. Publ., Hackensack, NJ, 2008, pp. 105–193. http://dx.doi.org/10.1142/97898127940550003 Google Scholar
[13] Steel, J. R., Scales in K(ℝ). In: Games, scales, and Suslin cardinals. The Cabal Seminar. Vol. I, Lect. Notes Log., 31, Assoc. Symbol. Logic, Chicago, IL, 2008, pp. 176–208. http://dx.doi.org/10.1017/CBO9780511546488.011 CrossRefGoogle Scholar
[14] Steel, J. R., Scales in K(ℝ) at the end of a weak gap. J. Symbolic Logic, 73(2008), no. 2, 369–390. http://dx.doi.org/10.2178/jsl/1208359049 CrossRefGoogle Scholar
[15] Steel, J. R., The derived model theorem. In: Logic Colloquium 2006, Lect. Notes Log., Assoc. Symbol. Logic, Chicago, IL, 2009, pp. 280–327. http://dx.doi.org/10.1017/CBO9780511605321.014 CrossRefGoogle Scholar
[16] Steel, J. R., Core models with more Woodin cardinals. J. Symbolic Logic, 67(2002), no. 3, 1197–1226. http://dx.doi.org/10.2178/jsl/1190150159 CrossRefGoogle Scholar
[17] Woodin, W. H., Suitable extender models I. J. Math. Log. 10(2010), no. 1–2, 101–339. http://dx.doi.org/10.1142/S021906131000095X CrossRefGoogle Scholar