Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-15T01:42:33.527Z Has data issue: false hasContentIssue false
  • English
  • Français

A Note on Buchsbaum Rings and Localizations of Graded Domains

Published online by Cambridge University Press:  20 November 2018

U. Daepp  and
A. Evans
U. Daepp
Affiliation:
Michigan State University, East Lansing, Michigan
A. Evans
Affiliation:
Vassar College, Poughkeepsie, New York
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let R = ⊕i ≧0Ri be a graded integral domain, and let p ∈ Proj (R) be a homogeneous, relevant prime ideal. Let R(P) = {r/t| r ∈ Ri, t ∈ Ri\p} be the geometric local ring at p and let Rp = {r/t| r ∈ R, t ∈ R\p} be the arithmetic local ring at p. Under the mild restriction that there exists an element r1 ∈ R1\p, W. E. Kuan [2], Theorem 2, showed that r1 is transcendental over R(P) and

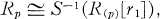
where S is the multiplicative system R\p. It is also demonstrated in [2] that R(P) is normal (regular) if and only if Rp is normal (regular). By looking more closely at the relationship between R(P) and R(P), we extend this result to Cohen-Macaulay (abbreviated C M.) and Gorenstein rings.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 32 , Issue 5 , 01 October 1980 , pp. 1244 - 1249
Copyright
Copyright © Canadian Mathematical Society 1980

References

1. Grothendieck, A., Local cohomology, Springer Lecture Notes 41 (Berlin, Heidelberg, 1967).Google Scholar
2. Kuan, W. E., Some results on normality of a graded ring, Pacific J. Math. 64 (1976), 455–463.Google Scholar
3. Lech, C., Inequalities related to certain couples of local rings, Acta. Math. 112 (1964), 69–89.Google Scholar
4. Matlis, E., The multiplicity and reduction number of a one dimensional local ring, Proc. London Math. Soc. (3) 26 (1973), 273–288.Google Scholar
5. Matsumura, H., Commutative algebra (W. A. Benjamin, New York, 1970).Google Scholar
6. Northcott, D. G., Ideal theory (Cambridge Univ. Press, 1953).CrossRefGoogle Scholar
7. Northcott, D. G., An introduction to homologuai algebra (Cambridge Univ. Press, 1962).Google Scholar
8. Peskine, C. and Szpiro, L., Dimension projective finie et cohomologie local, IHES Publ. Math. 42.Google Scholar
9. Stuckrad, J., Über die kohomologische Charakterisierung von Buchsbaum-Moduln, Math. Nachr. (to appear).CrossRefGoogle Scholar
10. Stückrad, J. and Vogel, W., Eine Verallgemeinerung der Cohen-Macaulay Ringe und Anwendungen auf ein Problem der Multiplizitdtstheorie, J. Math. Kyoto Univ. 13–3 (1973), 513–528.Google Scholar
11. Stückrad, J. and Vogel, W., Über das Amsterdamer Programm von IV. Gröbner, Monatshefte für Math. 78 (1974), 433–445.Google Scholar
12. Vogel, W., A non-zero divisor characterization of Buchsbaum modules, Preprint.CrossRefGoogle Scholar
13. Watanabe, K., Ishikawa, T., Tachibana, S., and Otsuka, K., On tensor products of Gorenstem rings, J. Math. Kyoto Univ., 9–3 (1969), 413–423.Google Scholar