No CrossRef data available.
Article contents
A Note on Certain Spaces with Bases (mod K)
Published online by Cambridge University Press: 20 November 2018
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
In this note all spaces are assumed to be regular T1 spaces and all undefined terms and notations may be found in [8], In particular let cl(A) denote the closure of the set A and let Z+ denote the set of natural numbers.
Definition 1. Let X be a topological space and  a covering of X by compact sets. An open covering
a covering of X by compact sets. An open covering 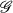 of X is said to be a basis (mod K) if whenever
of X is said to be a basis (mod K) if whenever 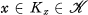 and an open set V contains Kx, then there exists
and an open set V contains Kx, then there exists  such that
such that 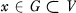 . In such a case X is written as the ordered triple
. In such a case X is written as the ordered triple 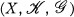 .
.
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1975
References
1.
Arhangel'skiï, A. V., On a class of spaces containing all metric and all locally bicompact spaces,
Sov. Math. Dokl. 4 (1963), 1051–1055.Google Scholar
2.
Bennett, H. R. and Lutzer, D. J., A note on weak 0-refinability,
General Topology and Appl. 2 (1972), 49–54.Google Scholar
5.
Burke, D. K., A nondevelopable locally compact Hausdorff space with a G'diagonal,
General Topology and Appl. 2 (1972), 287–292.Google Scholar
6.
Céder, J. G., Some generalizations of metric spaces,
Pacific J. Math. 11 (1961), 105–126.Google Scholar
7.
Creede, G. D. D., Concerning semi-stratifiable spaces,
Pacific J. Math. 32 (1970), 47–54.Google Scholar
9.
Heath, R. W., Arcwise connectedness in semi-metric spaces,
Pacific J. Math. 12 (1962), 1301–1319.Google Scholar
11.
Martin, H. W., Metrization and submetrization of topological spaces, Ph.D. Thesis, University of Pittsburgh, 1973.Google Scholar
12.
Michael, E., On Nagamïs espaces and some related matters, Proc. Wash. S. Univ. Conf., 1970, 13–18.Google Scholar
13.
Morita, K. and Hanai, S., Closed mappings and metric spaces,
Proc. Jap. Acad. 32 (1956), 10–14.Google Scholar
15.
Stone, A. H., Metrizability of decomposition spaces, Proc. Amer. Math. Soc. 7 (1956), 690–700.Google Scholar
16.
Worrell, J. M. and Wicke, H. H., Characterizations of developable topological spaces,
Can. J. Math. 17 (1965), 820–830.Google Scholar

