Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-01-13T00:57:04.750Z Has data issue: false hasContentIssue false
  • English
  • Français

A Note on Non-Distributive Sublattices of Degrees and Hyperdegrees

Published online by Cambridge University Press:  20 November 2018

S. K. Thomason
S. K. Thomason*
Affiliation:
Simon Fraser University, Burnaby, B.C. University of California, Berkeley, California
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In (1, §§ 2.3 and 2.4) we proved that certain distributive lattices are simultaneously lattice-embeddable in the degrees of recursive unsolvability and in the hyperdegrees. Let ℒ be the non-distributive lattice {0,1, a0, a1,…}, where ai ∪ aj = 1 and ai ∩ aj = 1 whenever i ≠ j. We shall prove the following theorem.

THEOREM. The lattice ℒ is simultaneously lattice-embeddable in the degrees and hyperdegrees.

For A ⊆ N, let deg(A) and hyp(A) be the degree and hyperdegree of A, respectively. To prove the theorem we must construct hyperarithmetically incomparable sets A0, A1, … such that for Δ = deg, hypand for all distinct i, j:

1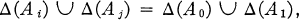

2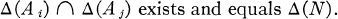

Now, if each 〈Ai, Aj〉 were a generic pair in the sense of (1), then (2) would hold.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 21 , 1969 , pp. 147 - 148
Copyright
Copyright © Canadian Mathematical Society 1969

References

1. Thomason, S. K., The forcing method and the upper semi-lattice of hyperdegrees, Trans. Amer. Math. Soc. 129 (1967), 38–57.Google Scholar