Article contents
A Note on the mod 2 Cohomology of BŜOn〈l6〉
Published online by Cambridge University Press: 20 November 2018
Extract
Recall BSOn is the classifying space for the special orthogonal group of rank n. It is well known that the mod 2 cohomology ring of BSOn is given as follows:
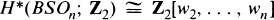
where wi is the i-th mod 2 Stiefel-Whitney class. For the 3-connective cover of BSOn, BSpinn, Quillen in [4] has determined H*(BSpinn) completely for all n. Let BŜOn〈8〉, BŜOn〈16〉 be the classifying spaces for n-plane spin bundle ξ satisfying w4(ξ) = 0 and w4(ξ) = w8(ξ) = 0 respectively. This note follows the method of A. Borel [2] and gives the mod 2 cohomology ring of BŜOn〈8〉 and BŜOn〈16〉 for small n. In particular we answer the question “when is H*(BŜOn〈8〉; Z2), or H*(BŜOn〈16〉; Z2) a polynomial algebra?”
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1985
References
- 6
- Cited by


