Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-15T18:53:16.627Z Has data issue: false hasContentIssue false
  • English
  • Français

The Number of 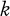-Coloured Graphs

Published online by Cambridge University Press:  20 November 2018

David A. Klarner
David A. Klarner*
Affiliation:
McMaster University, Hamilton, Ontario; Technical University, Eindhoven, The Netherlands
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we describe an algorithm for finding the number of non-isomorphic 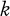-coloured graphs with n nodes and e edges. We use Pόlya's fundamental enumeration theorem (in a form similar to that given by de Bruijn (see 1)) which reduces the problem to finding the cycle index for a certain permutation group. Harary (3) followed this same program for bi-coloured graphs, but failed to find the cycle index of the relevant group for general 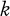-coloured graphs.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 20 , 1968 , pp. 1344 - 1352
Copyright
Copyright © Canadian Mathematical Society 1968

Footnotes

This paper was written while the author was a post-doctoral fellow at McMaster University, Hamilton, Ontario, Canada, 1967.

References

1. Beckenbach, Edwin F. (editor), Applied combinatorial mathematics, Chapter 5, “Pôlya's theory of counting”, by de Bruijn, N. G. pp. 144–184 (Wiley, New York, 1964).Google Scholar
2. de Bruijn, N. G. Generalization of Pôlya's fundamental theorem in enumerative combinatorial analysis, Nederl. Akad. Wetensch. Proc. Ser. A 62 Indag. Math. 21 (1959), 59–69.Google Scholar
3. Harary, F., On the number of bi-colored graphs, Pacific J. Math. 8 (1958), 743–755.Google Scholar
4. Read, R. C., The number of k-coloured graphs on labelled nodes, Can. J. Math. 12 (1960), 410–414.Google Scholar
5. Robinson, R. W., Enumeration of colored graphs, J. Combinatorial Theory 4 (1968), 181–190.Google Scholar
6. Wright, E. M., Counting coloured graphs. I, Can. J. Math. 13 (1961), 683–693.Google Scholar
7. Wright, E. M., Counting coloured graphs. II, Can. J. Math. 16 (1964), 128–135.Google Scholar