No CrossRef data available.
Published online by Cambridge University Press: 20 November 2018
(1.1) The conjugate function on locally compact abelian groups. Let G be a locally compact abelian group with character group Ĝ. Let μ denote a Haar measure on G such that μ(G) = 1 if G is compact. (Unless stated otherwise, all the measures referred to below are Haar measures on the underlying groups.) Suppose that Ĝ contains a measurable order P: P + P ⊆P; PU(-P)= Ĝ; and P⋂(—P) =﹛0﹜. For ƒ in ℒ2(G), the conjugate function of f (with respect to the order P) is the function 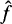 whose Fourier transform satisfies the identity
whose Fourier transform satisfies the identity 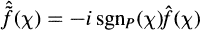 for almost all χ in Ĝ, where sgnP(χ)= 0, 1, or —1, according as χ =0, χ ∈ P\\﹛0﹜, or χ ∈ (—P)\﹛0﹜.
for almost all χ in Ĝ, where sgnP(χ)= 0, 1, or —1, according as χ =0, χ ∈ P\\﹛0﹜, or χ ∈ (—P)\﹛0﹜.