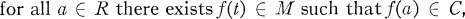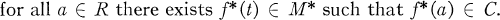Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Chacron, M
1970.
On a theorem of Procesi.
Journal of Algebra,
Vol. 15,
Issue. 2,
p.
225.
Bell, H. E.
1975.
Some commutativity results for rings with two-variable constraints.
Proceedings of the American Mathematical Society,
Vol. 53,
Issue. 2,
p.
280.
Chacron, M.
1976.
A commutativity theorem for rings.
Proceedings of the American Mathematical Society,
Vol. 59,
Issue. 2,
p.
211.
Bell, Howard E.
1977.
A Commutativity Theorem for Near-Rings.
Canadian Mathematical Bulletin,
Vol. 20,
Issue. 1,
p.
25.
Chacron, M
1977.
Algebraic Φ-rings extensions of bounded index.
Journal of Algebra,
Vol. 44,
Issue. 2,
p.
370.
Bell, H. E.
1980.
On commutativity of periodic rings and near-rings.
Acta Mathematica Academiae Scientiarum Hungaricae,
Vol. 36,
Issue. 3-4,
p.
293.
Richoux, Anthony
1980.
A Commutativity Theorem for Division Rings.
Canadian Mathematical Bulletin,
Vol. 23,
Issue. 2,
p.
241.
Bell, Howard E.
1981.
On quasi-periodic rings.
Archiv der Mathematik,
Vol. 36,
Issue. 1,
p.
502.
McKenzie, Ralph
1982.
Residually small varieties ofK-algebras.
Algebra Universalis,
Vol. 14,
Issue. 1,
p.
181.
Cherubini, A.
and
Varisco, A.
1986.
Rings satisfying certain conditions either on subsemigroups or on endomorphisms.
Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics,
Vol. 40,
Issue. 2,
p.
194.
Bell, Howard E.
Janjić, Milan
and
Psomopoulos, Evagelos
1990.
On Rings with Powers Commuting on Subsets.
Results in Mathematics,
Vol. 18,
Issue. 1-2,
p.
1.
Hirano, Yasuyuki
1991.
Some characterizations of π-regular rings with no infinite trivial subring.
Proceedings of the Edinburgh Mathematical Society,
Vol. 34,
Issue. 1,
p.
1.
Bell, Howard E.
and
Klein, Abraham A.
1992.
On rings with engel cycles, II.
Results in Mathematics,
Vol. 21,
Issue. 3-4,
p.
265.
Bell, Howard E.
1994.
ON PSEUDO-COMMUTATMTY AND COMMUTATIVITY IN RINGS.
Quaestiones Mathematicae,
Vol. 17,
Issue. 2,
p.
173.
Spiegel, Eugene
1999.
Algebraic radicals and incidence algebras.
Journal of Discrete Mathematical Sciences and Cryptography,
Vol. 2,
Issue. 2-3,
p.
197.
Bell*, Howard E.
and
Klein, Abraham A.
2001.
COMBINATORIAL COMMUTATIVITY AND FINITENESS CONDITIONS FOR RINGS.
Communications in Algebra,
Vol. 29,
Issue. 7,
p.
2935.
Bell, Howard E.
2002.
A Near-Commutativity Property for Rings.
Results in Mathematics,
Vol. 42,
Issue. 1-2,
p.
28.
Bell, Howard E.
and
Klein, Abraham A.
2008.
Extremely noncommutative elements in rings.
Monatshefte für Mathematik,
Vol. 153,
Issue. 1,
p.
19.
Bell, H. E.
and
Klein, A. A.
2009.
On almost-quasi-commutative rings.
Acta Mathematica Hungarica,
Vol. 122,
Issue. 1-2,
p.
121.
Chen, Huanyin
Kose, Handan
and
Kurtulmaz, Yosum
2014.
EXTENSIONS OF STRONGLY π-REGULAR RINGS.
Bulletin of the Korean Mathematical Society,
Vol. 51,
Issue. 2,
p.
555.