Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Chomsky, N.
and
Schützenberger, M.P.
1959.
Computer Programming and Formal Systems.
Vol. 26,
Issue. ,
p.
118.
Uchiyama, Saburô
1960.
On the Thue-Siegel-Roth theorem, III.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 36,
Issue. 1,
Fenna, D.
1961.
Rational approximation with series.
Journal of the Australian Mathematical Society,
Vol. 2,
Issue. 1,
p.
107.
Chomsky, N.
and
Schützenberger, M.P.
1963.
Computer Programming and Formal Systems.
Vol. 35,
Issue. ,
p.
118.
Armitage, J.V
1968.
The Thue-Siegel-Roth theorem in characteristic p.
Journal of Algebra,
Vol. 9,
Issue. 2,
p.
183.
Osgood, Charles F.
1973.
An effective lower bound on the “Diophantine approximation” of algebraic functions by rational functions.
Mathematika,
Vol. 20,
Issue. 1,
p.
4.
Osgood, Charles F
1975.
Effective bounds on the “diophantine approximation” of algebraic functions over fields of arbitrary characteristic and applications to differential equations.
Indagationes Mathematicae (Proceedings),
Vol. 78,
Issue. 2,
p.
105.
Osgood, Charles F.
1977.
Contributions to Algebra.
p.
321.
Mahler, K
1982.
Fifty years as a mathematician.
Journal of Number Theory,
Vol. 14,
Issue. 2,
p.
121.
Sieburg, Hans -Bernd
1984.
Algebraically independent values of Liouville-von Neumann series overQV-fields.
Archiv der Mathematik,
Vol. 43,
Issue. 3,
p.
229.
Voloch, J. F.
1988.
Diophantine approximation in positive characteristic.
Periodica Mathematica Hungarica,
Vol. 19,
Issue. 3,
p.
217.
Lasjaunias, Alain
1997.
Diophantine Approximation and Continued Fraction Expansions of Algebraic Power Series in Positive Characteristic.
Journal of Number Theory,
Vol. 65,
Issue. 2,
p.
206.
Lasjaunias, Alain
1999.
Continued Fractions for Algebraic Formal Power Series over a Finite Base Field.
Finite Fields and Their Applications,
Vol. 5,
Issue. 1,
p.
46.
Thakur, Dinesh S.
1999.
Diophantine Approximation Exponents and Continued Fractions for Algebraic Power Series.
Journal of Number Theory,
Vol. 79,
Issue. 2,
p.
284.
Lasjaunias, Alain
2002.
Finite Fields with Applications to Coding Theory, Cryptography and Related Areas.
p.
220.
Thakur, Dinesh S.
2004.
Algebra, Arithmetic and Geometry with Applications.
p.
757.
Chaichana, Tuangrat
and
Laohakosol, Vichian
2007.
Independence of continued fractions in the field of Laurent series.
Periodica Mathematica Hungarica,
Vol. 55,
Issue. 1,
p.
35.
Thakur, Dinesh S.
Wen, Zhi-Ying
Yao, Jia-Yan
and
Zhao, Liang
2011.
Transcendence in positive characteristic and special values of hypergeometric functions.
Journal für die reine und angewandte Mathematik (Crelles Journal),
Vol. 2011,
Issue. 657,
Ayadi, K.
Hbaib, M.
and
Mahjoub, F.
2013.
Diophantine Approximation for Certain
Algebraic Formal Power Series in Positive
Characteristic.
Canadian Mathematical Bulletin,
Vol. 56,
Issue. 4,
p.
673.
Chen, Huei-Jeng
2013.
Distribution of Diophantine approximation exponents for algebraic quantities in finite characteristic.
Journal of Number Theory,
Vol. 133,
Issue. 11,
p.
3620.
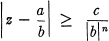 for every pair of integers a, b with b ≠ 0.
for every pair of integers a, b with b ≠ 0.