Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-14T05:16:39.545Z Has data issue: false hasContentIssue false
  • English
  • Français

On Branched Coverings of S3

Published online by Cambridge University Press:  20 November 2018

Gerhard Burde
Gerhard Burde*
Affiliation:
Mathematisches Seminar der Johann Wolfgang Goethe-Universität, Frankfurt, West Germany
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In [3] Fox studied a certain class of irregular coverings of S3 branched along some knot or link which turned out to be homotopy spheres. By a simple geometric construction, it is shown in this paper that these homotopy spheres are just 3-spheres, provided that the group of the knot or link k in question cannot be generated by a number of Wirtinger generators smaller than the minimal number of bridges of this knot or link. The knots and links with two bridges provide examples for such coverings. In the covering sphere there is a link 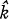covering k. With the help of braid automorphisms, 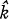can be determined. Figure 3 shows a link 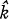in a 5-sheeted covering over k = 41. Links over 31 and 61 in 3-sheeted coverings were determined by Kinoshita [5] by a different method. The method used here is applicable to these cases and confirms his results.

Type
Research Article
Information
Canadian Journal of Mathematics , Volume 23 , Issue 1 , February 1971 , pp. 84 - 89
Copyright
Copyright © Canadian Mathematical Society 1971

References

1. Artin, E., Théorie der Zôpfe, Abh. Math. Sem. Hamburg Univ. 4 (1926), 47–72.Google Scholar
2. Burde, G., ZurThéorie der Zôpfe, Math. Ann. 151 (1963), 101–107.Google Scholar
3. Fox, R. H., Construction of simply connected 3-manifolds, Topology of 3-manifolds and related topics, Proc. The Univ. of Georgia Institute, 1961, pp. 213–216 (Prentice-Hall, Englewood Cliffs, N. J., 1962).Google Scholar
4. Fox, R. H., Metacyclic invariants of knots and links, Can. J. Math. 22 (1970), 193–201.Google Scholar
5. Kinoshita, S., On irregular branched covering spaces of a kind of knots, Notices Amer. Math. Soc. 14 (1967), 924.Google Scholar
6. Reidemeister, K., Knoten und Verkettungen, Math. Z. 29 (1929), 713–729.Google Scholar
7. Reidemeister, K., Knotentheorie, Ergebnisse der Mathematik und ihrerGrenzgebiete, Band 1 (Springer- Verlag, Berlin-Gôttingen-Heidelberg, 1932).Google Scholar
8. Reidemeister, K., Knoten und Geflechte, Nachr.Akad.Wiss.Gôttingen Math.-Phys. Kl. II 5 (1960), 105–115.Google Scholar
9. Schubert, H., Knoten mit zwei Brucken, Math. Z. 65 (1956), 133–170 Google Scholar