Article contents
On Cabled Knots and Vassiliev Invariants (Not) Contained in Knot Polynomials
Published online by Cambridge University Press: 20 November 2018
Abstract
It is known that the Brandt–Lickorish–Millett–Ho polynomial 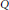 $Q$ contains Casson's knot invariant. Whether there are (essentially) other Vassiliev knot invariants obtainable from
$Q$ contains Casson's knot invariant. Whether there are (essentially) other Vassiliev knot invariants obtainable from 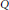 $Q$ is an open problem. We show that this is not so up to degree 9. We also give the (apparently) first examples of knots not distinguished by 2-cable HOMFLY polynomials which are not mutants. Our calculations provide evidence of a negative answer to the question whether Vassiliev knot invariants of degree
$Q$ is an open problem. We show that this is not so up to degree 9. We also give the (apparently) first examples of knots not distinguished by 2-cable HOMFLY polynomials which are not mutants. Our calculations provide evidence of a negative answer to the question whether Vassiliev knot invariants of degree 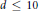 $d\,\le \,10$ are determined by the HOMFLY and Kauffman polynomials and their 2-cables, and for the existence of algebras of such Vassiliev invariants not isomorphic to the algebras of their weight systems.
$d\,\le \,10$ are determined by the HOMFLY and Kauffman polynomials and their 2-cables, and for the existence of algebras of such Vassiliev invariants not isomorphic to the algebras of their weight systems.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2007
References
- 10
- Cited by


