Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-27T09:43:33.910Z Has data issue: false hasContentIssue false
  • English
  • Français

On certain Tannakian categories of integrable connections over Kähler manifolds

Part of: Abelian varieties and schemes Cycles and subschemes Global differential geometry Modules, bimodules and ideals

Published online by Cambridge University Press:  21 April 2021

Indranil Biswas ,
João Pedro dos Santos ,
Sorin Dumitrescu  and
Sebastian Heller
Indranil Biswas*
Affiliation:
School of Mathematics, Tata Institute of Fundamental Research, Homi Bhabha Road, Mumbai400005, India
João Pedro dos Santos
Affiliation:
Sorbonne Université, Institut de Mathématiques de Jussieu–Paris Rive Gauche, 4 place Jussieu, Case 247, 75252Paris Cedex 5, France e-mail: joao_pedro.dos_antos@yahoo.com
Sorin Dumitrescu
Affiliation:
Université Côte d’Azur, CNRS, LJAD, France e-mail: dumitres@unice.fr
Sebastian Heller
Affiliation:
Institut für Differentialgeometrie, Leibniz Universität Hannover, Welfengarten 1, 30167Hannover, Germany e-mail: seb.heller@gmail.com
*
e-mail: indranil@math.tifr.res.in
Get access Rights & Permissions [Opens in a new window]

Abstract

Given a compact Kähler manifold X, it is shown that pairs of the form 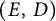$(E,\, D)$ , where E is a trivial holomorphic vector bundle on X, and D is an integrable holomorphic connection on E, produce a neutral Tannakian category. The corresponding pro-algebraic affine group scheme is studied. In particular, it is shown that this pro-algebraic affine group scheme for a compact Riemann surface determines uniquely the isomorphism class of the Riemann surface.

Keywords

Integrable holomorphic connectionHiggs bundleneutral Tannakian categorycomplex torusTorelli theorem

MSC classification

Primary: 53C07: Special connections and metrics on vector bundles (Hermite-Einstein-Yang-Mills)
Secondary: 14C34: Torelli problem 16D90: Module categories ; module theory in a category-theoretic context; Morita equivalence and duality 14K20: Analytic theory; abelian integrals and differentials
Type
Article
Information
Canadian Journal of Mathematics , Volume 74 , Issue 4 , August 2022 , pp. 1034 - 1061
Check for updates
Copyright
© Canadian Mathematical Society 2021

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

The first- and third-named authors were partially supported by the French government through the UCAJEDI Investments in the Future project managed by the National Research Agency (ANR) with the reference number ANR2152IDEX201. The first-named author is partially supported by a J. C. Bose Fellowship, and school of mathematics, TIFR, is supported by 12-R&D-TFR-5.01-0500. The fourth-named author is supported by the DFG grant HE 6829/3-1 of the DFG priority program SPP 2026 Geometry at Infinity.

References

Arbarello, E., Cornalba, M., Griffiths, P. A., and Harris, J., Geometry of algebraic curves. Vol. I , Grundlehren der Mathematischen Wissenschaften, 267, Springer-Verlag, New York, 1985.CrossRefGoogle Scholar
Atiyah, M. F., On the Krull–Schmidt theorem with application to sheaves. Bull. Soc. Math. France 84(1956), 307–317.CrossRefGoogle Scholar
Atiyah, M. F., Complex analytic connections in fibre bundles. Trans. Amer. Math. Soc. 85(1957), 181–207.CrossRefGoogle Scholar
Biswas, I. and Dumitrescu, S., The monodromy map from differential systems to character variety is generically immersive. Preprint, 2021. arXiv:2002.05927 Google Scholar
Biswas, I., Dumitrescu, S., and Heller, S., Irreducible flat $\ SL\left(2,\mathbb{R}\right)$ -connections on the trivial holomorphic bundle . J. Math. Pures Appl. 149(2021), 1–27.CrossRefGoogle Scholar
Biswas, I. and Gómez, T. L., Connections and Higgs fields on a principal bundle. Ann. Glob. Anal. Geom. 33(2008), 19–46.CrossRefGoogle Scholar
Biswas, I., Hai, P. H., and dos Santos, J. P., On the fundamental group schemes of certain quotient varieties. Tohoku Math. J. Preprint, 2020. arXiv:1809.06755v2.CrossRefGoogle Scholar
Biswas, I. and Subramanian, S., Flat holomorphic connections on principal bundles over a projective manifold. Trans. Amer. Math. Soc. 356(2004), 3995–4018.CrossRefGoogle Scholar
Borel, A., Grivel, P.-P., Kaup, B., Haefliger, A., Malgrange, B., and Ehlers, F., Algebraic D-modules . Perspectives in Mathematics, 2, Academic Press, Inc., Boston, MA, 1987.Google Scholar
Bourbaki, N., Algebra. I. Chapters 1–3 . Elements of Mathematics (Berlin), Springer-Verlag, Berlin, 1989.Google Scholar
Calsamiglia, G., Deroin, B., Heu, V., and Loray, F., The Riemann–Hilbert mapping for $\ sl(2)$ -systems over genus two curves . Bull. Soc. Math. Fr. 147(2019), 159–195.CrossRefGoogle Scholar
Corlette, K., Flat $\ G$ -bundles with canonical metrics . J. Diff. Geom. 28(1988), 361–382.Google Scholar
Deligne, P., Milne, J. S., Ogus, A., and Shih, K.-Y., Hodge cycles, motives, and Shimura varieties . Lecture Notes in Mathematics, 900, Springer-Verlag, Berlin and New York, 1982.CrossRefGoogle Scholar
Esnault, H., Hai, P. H., and Sun, X., On Nori’s fundamental group scheme . In: Kapranov, M., Manin, Y. I., Moree, P., Kolyada, S., and Potyagailo, L. (eds.), Geometry and dynamics of groups and spaces, Progress in Mathematics, 265, Birkhäuser, Basel, 2008, pp. 377–398.CrossRefGoogle Scholar
Fischer, G., Complex analytic geometry . Lecture Notes in Mathematics, 538, Springer-Verlag, Berlin and New York, 1976.CrossRefGoogle Scholar
Freyd, P., Abelian categories. An introduction to the theory of functors . Harper’s Series in Modern Mathematics, Harper & Row Publishers, New York 1964.Google Scholar
Griffiths, P. and Harris, J., Principles of algebraic geometry . Wiley Classics Library, John Wiley & Sons, Inc., New York, 1994, Reprint of the 1978 original.CrossRefGoogle Scholar
Hochschild, G., Basic theory of algebraic groups and Lie algebras . Graduate Texts in Mathematics, 75, Springer-Verlag, New York and Berlin, 1981.CrossRefGoogle Scholar
Huckleberry, A. T. and Margulis, G. A., Invariant analytic hypersurfaces. Invent. Math. 71(1983), 235–240.CrossRefGoogle Scholar
Katz, N. M., An overview of Deligne’s work on Hilbert’s twenty-first problem . In: Mathematical developments arising from Hilbert problems, (Felix E. Browder) Proceedings of Symposia in Pure Mathematics, Vol. XXVIII, Northern Illinois University, DeKalb, IL, 1974, American Mathematical Society, Providence, RI, 1976, pp. 537–557.CrossRefGoogle Scholar
Kobayashi, S., Differential geometry of complex vector bundles . Publications of the Mathematical Society of Japan, 15, Kanô Memorial Lectures, 5, Princeton University Press, Princeton, NJ, 1987.CrossRefGoogle Scholar
Lübke, M. and Teleman, A., The Kobayashi–Hitchin correspondence . World Scientific Publishing Co. Inc., River Edge, NJ, 1995.CrossRefGoogle Scholar
Nori, M. V., The fundamental group–scheme. Proc. Ind. Acad. Sci. (Math. Sci.) 91(1982), 73–122.CrossRefGoogle Scholar
Raynaud, M., Anneaux locaux henséliens . Lecture Notes in Mathematics, 169, Springer-Verlag, Berlin and New York, 1970.CrossRefGoogle Scholar
Saavedra Rivano, N., Catégories Tannakiennes . Lecture Notes in Mathematics, 265, Springer-Verlag, Berlin and New York, 1972.CrossRefGoogle Scholar
Séminaire Henri Cartan, 13th year: 1960/61. Familles d’espaces complexes et fondements de la géométrie analytique. Fasc. 1 et 2: Exp. 1–21 , 2nd corrected ed. Secrétariat de mathématique de l'Ecole Normale Supérieure, Paris, 1962.Google Scholar
Seshadri, C. S., Space of unitary vector bundles on a compact Riemann surface. Ann. of Math. 85(1967), 303–336.CrossRefGoogle Scholar
Simpson, C. T., Constructing variations of Hodge structure using Yang–Mills theory and applications to uniformization. J. Amer. Math. Soc. 1(1988), 867–918.CrossRefGoogle Scholar
Simpson, C. T., Higgs bundles and local systems. Inst. Hautes Études Sci. Publ. Math. 75(1992), 5–95.CrossRefGoogle Scholar
Uhlenbeck, K. and Yau, S.-T., On the existence of Hermitian–Yang–Mills connections in stable vector bundles. Comm. Pure Appl. Math. 39(1986), 257–293.CrossRefGoogle Scholar
Waterhouse, W. C., Introduction to affine group schemes . Graduate Texts in Mathematics, 66, Springer-Verlag, New York and Berlin, 1979.CrossRefGoogle Scholar