Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Miyazaki, Hiroshi
1952.
A note on paracompact spaces.
Tohoku Mathematical Journal,
Vol. 4,
Issue. 1,
Arens, Richard
1953.
Extension of Coverings, of Pseudometrics, and of
Linear-Space-Valued Mappings.
Canadian Journal of Mathematics,
Vol. 5,
Issue. ,
p.
211.
Morita, Kiiti
1954.
On spaces having the weak topology with respect to closed coverings, II.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 30,
Issue. 8,
Nagami, Keiô
1954.
Baire Sets, Borel Sets and Some Typical Semi-Continuous Functions.
Nagoya Mathematical Journal,
Vol. 7,
Issue. ,
p.
85.
Iséki, Kiyoshi
1954.
A note on countably paracompact spaces.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 30,
Issue. 5,
Gillman, Leonard
and
Henriksen, Melvin
1954.
Concerning rings of continuous functions.
Transactions of the American Mathematical Society,
Vol. 77,
Issue. 2,
p.
340.
Ball, B. J.
1954.
Countable paracompactness in linearly ordered spaces.
Proceedings of the American Mathematical Society,
Vol. 5,
Issue. 2,
p.
190.
Nagami, Keiô
1955.
Paracompactness and Strong Screenability.
Nagoya Mathematical Journal,
Vol. 8,
Issue. ,
p.
83.
Michael, Ernest
1955.
Point-Finite And Locally Finite Coverings.
Canadian Journal of Mathematics,
Vol. 7,
Issue. ,
p.
275.
Ellen Rudin, Mary
1955.
Countable Paracompactness and Souslin's Problem.
Canadian Journal of Mathematics,
Vol. 7,
Issue. ,
p.
543.
McAuley, Louis F.
1956.
Paracompactness and an example due to F. B. Jones.
Proceedings of the American Mathematical Society,
Vol. 7,
Issue. 6,
p.
1155.
Kasahara, Shouro
1956.
Note on the Lebesgue property in uniform spaces, II.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 32,
Issue. 4,
Mansfield, M. J.
1957.
Some generalizations of full normality.
Transactions of the American Mathematical Society,
Vol. 86,
Issue. 2,
p.
489.
Mansfield, M. J.
1957.
On Countably Paracompact Normal Spaces.
Canadian Journal of Mathematics,
Vol. 9,
Issue. ,
p.
443.
Hayashi, Yoshiaki
1957.
On Dowker's problem.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 33,
Issue. 7,
Michael, E.
1957.
Another note on paracompact spaces.
Proceedings of the American Mathematical Society,
Vol. 8,
Issue. 4,
p.
822.
Aquaro, Giovanni
1959.
Ricovrimenti aperti e strutture uniformi sopra uno spazio topologico.
Annali di Matematica Pura ed Applicata,
Vol. 47,
Issue. 1,
p.
319.
Morita, Kiiti
1961.
Note on paracompactness.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 37,
Issue. 1,
Suzuki, Jingoro
1963.
Some properties of completely normal and collectionwise normal spaces.
Proceedings of the Japan Academy, Series A, Mathematical Sciences,
Vol. 39,
Issue. 4,
1964.
Vol. 16,
Issue. ,
p.
175.
 is called a refinement of a covering U if every open set of X is contained in some open set of
is called a refinement of a covering U if every open set of X is contained in some open set of 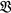 . The space X is called countably paracompact if every countable covering has a locally finite refinement.
. The space X is called countably paracompact if every countable covering has a locally finite refinement.