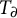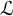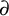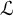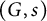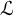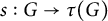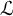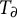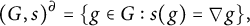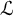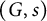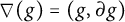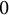1 Introduction
1.1 Background and motivation
Let us begin with some motivation and background for the general reader.
The notion of an algebraic D-group is due in full generality to Buium [Reference Buium4] and belongs entirely to algebraic geometry. It can be described as follows: let
![]() $(K,\partial )$
be a field of characteristic
$(K,\partial )$
be a field of characteristic
![]() $0$
equipped with a derivation
$0$
equipped with a derivation
![]() $\partial :K\to K$
. Then a (connected) algebraic D-group over
$\partial :K\to K$
. Then a (connected) algebraic D-group over
![]() $(K,\partial )$
is a (connected) algebraic group G over K, together with a lifting of
$(K,\partial )$
is a (connected) algebraic group G over K, together with a lifting of
![]() $\partial $
to a derivation
$\partial $
to a derivation
![]() $\partial ': O_{K}(G) \to O_{K}(G)$
of the structure sheaf
$\partial ': O_{K}(G) \to O_{K}(G)$
of the structure sheaf
![]() $O_{K}(G)$
of K, commuting with (or respecting) co-multiplication. When G is affine, we can replace the structure sheaf by the coordinate ring of G. There are other equivalent descriptions (as given later). One can think of an algebraic D-group as an algebraic group over a differential field, which is equipped with a certain kind of order-one differential equation. When the base field is
$O_{K}(G)$
of K, commuting with (or respecting) co-multiplication. When G is affine, we can replace the structure sheaf by the coordinate ring of G. There are other equivalent descriptions (as given later). One can think of an algebraic D-group as an algebraic group over a differential field, which is equipped with a certain kind of order-one differential equation. When the base field is
![]() $(\mathbb {C}(t), d/dt)$
, a geometric description of an algebraic D-group is a family
$(\mathbb {C}(t), d/dt)$
, a geometric description of an algebraic D-group is a family
![]() ${\mathcal G}\to S$
of complex algebraic groups over the affine line (with finitely many points removed), together with a suitable “Ehresmann connection,” namely lift of the vector field on S corresponding to
${\mathcal G}\to S$
of complex algebraic groups over the affine line (with finitely many points removed), together with a suitable “Ehresmann connection,” namely lift of the vector field on S corresponding to
![]() $d/dt$
to a vector field on the total space
$d/dt$
to a vector field on the total space
![]() ${\mathcal G}$
, respecting multiplication in the obvious sense. One of the main points of [Reference Buium4] is to show that the category of algebraic D-groups over K is the “same” as the category of finite-dimensional differential algebraic groups over K in the sense of Kolchin [Reference Kolchin12]. An algebraic D-group,
${\mathcal G}$
, respecting multiplication in the obvious sense. One of the main points of [Reference Buium4] is to show that the category of algebraic D-groups over K is the “same” as the category of finite-dimensional differential algebraic groups over K in the sense of Kolchin [Reference Kolchin12]. An algebraic D-group,
![]() $(G,s)$
over
$(G,s)$
over
![]() $(K,\partial )$
is associated with the solution set of the corresponding differential equation in a “universal” differential field
$(K,\partial )$
is associated with the solution set of the corresponding differential equation in a “universal” differential field
![]() $(L,\partial )$
extending K (which will be a subgroup of
$(L,\partial )$
extending K (which will be a subgroup of
![]() $G(L)$
). Moreover, Buium [Reference Buium4] has an exhaustive study of these finite-dimensional differential algebraic groups, yielding an account of (cases of) function field Mordell–Lang in characteristic
$G(L)$
). Moreover, Buium [Reference Buium4] has an exhaustive study of these finite-dimensional differential algebraic groups, yielding an account of (cases of) function field Mordell–Lang in characteristic
![]() $0$
. This was built on by Hrushovski [Reference Hrushovski8] using model-theoretic methods and generalized to positive characteristic.
$0$
. This was built on by Hrushovski [Reference Hrushovski8] using model-theoretic methods and generalized to positive characteristic.
The connection with model theory is that finite-dimensional differential groups, in the sense of Kolchin above, are precisely the finite-dimensional groups definable in differentially closed fields
![]() $(K, +, \cdot , \partial )$
, and various nontrivial model-theoretic results come into play (see [Reference Bouscaren2]). Moreover, algebraic groups over algebraically closed fields K are precisely definable groups in algebraically closed fields
$(K, +, \cdot , \partial )$
, and various nontrivial model-theoretic results come into play (see [Reference Bouscaren2]). Moreover, algebraic groups over algebraically closed fields K are precisely definable groups in algebraically closed fields
![]() $(K,+,\cdot )$
(see [Reference van den Dries22]).
$(K,+,\cdot )$
(see [Reference van den Dries22]).
The purpose of this paper is to generalize the relationships between algebraic groups, algebraic D-groups, and finite-dimensional differential algebraic groups, to other categories, sometimes provided by model theory. In one of these categories, Nash groups replace algebraic groups. The category of Nash groups lies properly in between the categories of real algebraic groups and (real) Lie groups. The model-theoretic connection is that these are precisely the groups definable in real closed fields. Likewise p-adic Nash groups, also treated in this paper are those definable in p-adically closed fields. So, among other things, we introduce the notion of a Nash D-group over a real closed differential field, likewise for p-adic analogues, and relate them to finite-dimensional definable groups in real closed (p-adically closed) fields equipped with a “generic” derivation. We also consider the case of pseudo-finite fields K, where definable groups are, up to a quotient by a finite normal subgroup, a finite index subgroup of
![]() $G(K)$
, for G an algebraic group over K (see [Reference Hrushovski and Pillay9]).
$G(K)$
, for G an algebraic group over K (see [Reference Hrushovski and Pillay9]).
From this point on, the paper is somewhat more technical, and assumes some knowledge of basic model theory. We will be repeating in different formalisms, the notions discussed in the last paragraphs.
1.2 The setting and main result
In [Reference Peterzil, Pillay and Point15], we initiated a study of definable groups in closed ordered differential fields (see [Reference Singer20]), and more generally in differential expansions of o-minimal structures, p-adically closed fields, pseudo-finite fields of characteristic
![]() $0$
, or topological fields which are models of an open theory (as in [Reference Kovacsis and Point13]).
$0$
, or topological fields which are models of an open theory (as in [Reference Kovacsis and Point13]).
In all of the above settings, we start with a suitable theory T in a language
![]() ${\mathcal {L}}$
, where T expands the theory of fields. We add a symbol
${\mathcal {L}}$
, where T expands the theory of fields. We add a symbol
![]() $\partial $
to the language to get
$\partial $
to the language to get
![]() ${\mathcal {L}}_\partial ={\mathcal {L}}\cup \{\partial \}$
. The
${\mathcal {L}}_\partial ={\mathcal {L}}\cup \{\partial \}$
. The
![]() ${\mathcal {L}}_\partial $
-theory
${\mathcal {L}}_\partial $
-theory
![]() $T\cup $
“
$T\cup $
“
![]() $\partial $
is a (compatible) derivation” will have a model companion which we call
$\partial $
is a (compatible) derivation” will have a model companion which we call
![]() $T_\partial $
.
$T_\partial $
.
The main theorems in [Reference Peterzil, Pillay and Point15] said that in all of these cases, if
![]() $\Gamma $
is a finite-dimensional group in a model of
$\Gamma $
is a finite-dimensional group in a model of
![]() $T_\partial $
, then there is an
$T_\partial $
, then there is an
![]() ${\mathcal {L}}$
-definable group G and an
${\mathcal {L}}$
-definable group G and an
![]() ${\mathcal {L}}_{\partial }$
-definable group embedding of
${\mathcal {L}}_{\partial }$
-definable group embedding of
![]() $\Gamma $
into G.
$\Gamma $
into G.
Here, we mostly follow the setting suggested by Fornasiero and Kaplan [Reference Fornasiero and Kaplan6], where we start with an
![]() ${\mathcal {L}}$
-theory T of an o-minimal expansion of a real closed field K, expand it in the language
${\mathcal {L}}$
-theory T of an o-minimal expansion of a real closed field K, expand it in the language
![]() ${\mathcal {L}}_\partial $
to the theory
${\mathcal {L}}_\partial $
to the theory
![]() $T^*$
of a T-compatible derivation
$T^*$
of a T-compatible derivation
![]() $\partial $
, and let
$\partial $
, and let
![]() $T_\partial $
be the model companion of
$T_\partial $
be the model companion of
![]() $T^*$
.
$T^*$
.
In [Reference Buium4], Buium introduced the notion of an algebraic D-group, namely a pair
![]() $(G,s)$
, where G is an algebraic group and
$(G,s)$
, where G is an algebraic group and
![]() $s:G\to \tau (G)$
a rational group section into the prolongation of G. In the setting of DCF
$s:G\to \tau (G)$
a rational group section into the prolongation of G. In the setting of DCF
![]() $_0$
(differentially closed fields of characteristic zero), it was shown (see [Reference Pillay18, Corollary 4.2] and [Reference Buium4]) that every finite-dimensional definable group is definably isomorphic to
$_0$
(differentially closed fields of characteristic zero), it was shown (see [Reference Pillay18, Corollary 4.2] and [Reference Buium4]) that every finite-dimensional definable group is definably isomorphic to
(
![]() $\nabla (g)=(g,\partial g)$
).
$\nabla (g)=(g,\partial g)$
).
Our goal here is to obtain analogous tools and theorems in the setting of
![]() $T_\partial $
. We first associate to every
$T_\partial $
. We first associate to every
![]() ${\mathcal {L}}$
-definable
${\mathcal {L}}$
-definable
![]() $C^1$
-manifold V, with respect to K, its prolongation, the bundle
$C^1$
-manifold V, with respect to K, its prolongation, the bundle
![]() $\tau (V)$
. We then note, as in the algebraic case, that when G is an
$\tau (V)$
. We then note, as in the algebraic case, that when G is an
![]() ${\mathcal {L}}$
-definable group over a differentially closed subfield of K, then so is
${\mathcal {L}}$
-definable group over a differentially closed subfield of K, then so is
![]() $\tau (G)$
, and the projection
$\tau (G)$
, and the projection
![]() $\pi :\tau (G)\to G$
a group homomorphism. An
$\pi :\tau (G)\to G$
a group homomorphism. An
![]() ${\mathcal {L}}$
-definable D-group is then a pair
${\mathcal {L}}$
-definable D-group is then a pair
![]() $(G,s)$
with G an
$(G,s)$
with G an
![]() ${\mathcal {L}}$
-definable group and
${\mathcal {L}}$
-definable group and
![]() $s:G\to \tau (G)$
an
$s:G\to \tau (G)$
an
![]() ${\mathcal {L}}$
-definable group section. Our main theorem (see Theorem 4.6) is the following.
${\mathcal {L}}$
-definable group section. Our main theorem (see Theorem 4.6) is the following.
Theorem Let
![]() $\Gamma $
be a finite-dimensional
$\Gamma $
be a finite-dimensional
![]() ${\mathcal {L}}_\partial $
-definable group in a model of
${\mathcal {L}}_\partial $
-definable group in a model of
![]() $T_\partial $
. Then there exists an
$T_\partial $
. Then there exists an
![]() ${\mathcal {L}}$
-definable D-group
${\mathcal {L}}$
-definable D-group
![]() $(G,s)$
such that
$(G,s)$
such that
![]() $\Gamma $
is definably isomorphic to
$\Gamma $
is definably isomorphic to
When T is a model complete theory of large fields in the language of fields (plus maybe constants), Tressl [Reference Tressl21] shows that the theory of models of T equipped with a derivation has a model companion. He also gave a uniform (in T) axiomatization of the model companion. Here, we treat two special cases: the case of p-adically closed fields and of pseudo-finite fields. We develop the notions of
![]() $\tau (G)$
and
$\tau (G)$
and
![]() $(G,s)$
, for an
$(G,s)$
, for an
![]() ${\mathcal {L}}$
-definable group G and prove the exact analogue of the above theorem for
${\mathcal {L}}$
-definable group G and prove the exact analogue of the above theorem for
![]() $T_\partial $
-definable groups (see Theorem 4.12). Along the way, we prove a p-adic analogue of an o-minimal theorem of Fornasiero and Kaplan (see Proposition A.1 in the Appendix).
$T_\partial $
-definable groups (see Theorem 4.12). Along the way, we prove a p-adic analogue of an o-minimal theorem of Fornasiero and Kaplan (see Proposition A.1 in the Appendix).
When K is a pseudo-finite field, we prove that every
![]() ${\mathcal {L}}_\partial $
-definable group
${\mathcal {L}}_\partial $
-definable group
![]() $\Gamma $
is virtually isogenous to
$\Gamma $
is virtually isogenous to
![]() $H_0\cap (H,s)^\partial $
, where
$H_0\cap (H,s)^\partial $
, where
![]() $(H,s)$
is an algebraic D-group over K and
$(H,s)$
is an algebraic D-group over K and
![]() $H_0$
a finite index subgroup of H (see Theorem 4.13).
$H_0$
a finite index subgroup of H (see Theorem 4.13).
Remark 1.1 The case of an arbitrary (not necessarily finite dimensional)
![]() ${\mathcal {L}}_\partial $
-definable group will be treated in a subsequent paper jointly with Silvain Rideau-Kikuchi.
${\mathcal {L}}_\partial $
-definable group will be treated in a subsequent paper jointly with Silvain Rideau-Kikuchi.
1.3 Preliminaries
We refer to Section 2 of [Reference Peterzil, Pillay and Point15] for all conventions and basic notions. Briefly, we always work in a sufficiently saturated structure and use the fact that o-minimal structures (and later, p-adically closed fields) are geometric structures in the sense of [Reference Hrushovski and Pillay9], to define
![]() $\dim _{\mathcal {L}}(a/k)$
as the
$\dim _{\mathcal {L}}(a/k)$
as the
![]() $acl_{\mathcal {L}}$
-dimension of a over k. The dimension of an
$acl_{\mathcal {L}}$
-dimension of a over k. The dimension of an
![]() ${\mathcal {L}}$
-definable set
${\mathcal {L}}$
-definable set
![]() $X\subseteq K^n$
is defined as the maximal
$X\subseteq K^n$
is defined as the maximal
![]() $\dim _{\mathcal {L}}(a/k)$
, for
$\dim _{\mathcal {L}}(a/k)$
, for
![]() $a\in X$
(or equivalently via cell decomposition). If we have
$a\in X$
(or equivalently via cell decomposition). If we have
![]() $\dim (a/B)=\dim X$
, for
$\dim (a/B)=\dim X$
, for
![]() $a\in X$
an
$a\in X$
an
![]() ${\mathcal {L}}$
-definable set over B (written also as
${\mathcal {L}}$
-definable set over B (written also as
![]() ${\mathcal {L}}(B)$
-definable), then we say that a is generic in X over B. A definable
${\mathcal {L}}(B)$
-definable), then we say that a is generic in X over B. A definable
![]() $Y\subseteq X$
is said to be large in X if
$Y\subseteq X$
is said to be large in X if
![]() $\dim (X\setminus Y)<\dim X$
(equivalently, Y contains every generic element of X over the parameters defining
$\dim (X\setminus Y)<\dim X$
(equivalently, Y contains every generic element of X over the parameters defining
![]() $X,Y$
).
$X,Y$
).
For a tuple
![]() $a=(a_1,\ldots , a_n)$
, we let
$a=(a_1,\ldots , a_n)$
, we let
![]() $\partial a=(\partial a_1,\ldots , \partial a_n)$
. To define the
$\partial a=(\partial a_1,\ldots , \partial a_n)$
. To define the
![]() ${\mathcal {L}}_\partial $
-dimension, for
${\mathcal {L}}_\partial $
-dimension, for
![]() $a\in K^n$
and
$a\in K^n$
and
![]() $k\subseteq K$
a differential subfield, we let
$k\subseteq K$
a differential subfield, we let
![]() $\dim _\partial (a/k)=\dim _{{\mathcal {L}}}(a,\partial a, \ldots , \partial ^n a,\ldots /k)$
(possibly infinite). The
$\dim _\partial (a/k)=\dim _{{\mathcal {L}}}(a,\partial a, \ldots , \partial ^n a,\ldots /k)$
(possibly infinite). The
![]() ${\mathcal {L}}_\partial $
-dimension of an
${\mathcal {L}}_\partial $
-dimension of an
![]() ${\mathcal {L}}_\partial $
-definable set
${\mathcal {L}}_\partial $
-definable set
![]() $X\subseteq K^n$
over k is the maximum
$X\subseteq K^n$
over k is the maximum
![]() $\dim _\partial (a/k)$
, as a varies in X.
$\dim _\partial (a/k)$
, as a varies in X.
2 Manifolds, tangent spaces, and tangent bundles
We fix an o-minimal expansion of a real closed field K in a language
![]() ${\mathcal {L}}$
. All definability in this section is in the o-minimal structure, allowing parameters.
${\mathcal {L}}$
. All definability in this section is in the o-minimal structure, allowing parameters.
We first recall the basic definition of a differentiable manifold and its tangent bundle in the o-minimal setting (for differentiability in this context, see [Reference van den Dries23, Section 7]).
Notation Let
![]() $U\subseteq K^r\times K^n$
be an open definable set, and
$U\subseteq K^r\times K^n$
be an open definable set, and
![]() $f:U\to K^m$
a definable
$f:U\to K^m$
a definable
![]() $C^1$
-map, written as
$C^1$
-map, written as
![]() $f(x,y)$
,
$f(x,y)$
,
![]() $f=(f_1,\ldots , f_m)$
. Given
$f=(f_1,\ldots , f_m)$
. Given
![]() $(a,b)\in U$
, we let
$(a,b)\in U$
, we let
![]() $(D_x f)_{(a,b)}:K^r\to K^m$
, and
$(D_x f)_{(a,b)}:K^r\to K^m$
, and
![]() $(D_y f)_{(a,b)}:K^n\to K^m$
denote the corresponding K-linear maps defined as follows:
$(D_y f)_{(a,b)}:K^n\to K^m$
denote the corresponding K-linear maps defined as follows:
![]() $(D_x f)_{(a,b)}$
is the
$(D_x f)_{(a,b)}$
is the
![]() $m\times r$
matrix of partial derivatives
$m\times r$
matrix of partial derivatives
 $$ \begin{align*}\left (\frac{\partial f_i}{\partial x_j}(a,b)\right )_{1\leq i\leq m, 1\leq j\leq r},\end{align*} $$
$$ \begin{align*}\left (\frac{\partial f_i}{\partial x_j}(a,b)\right )_{1\leq i\leq m, 1\leq j\leq r},\end{align*} $$
and
![]() $(D_y f)_{(a,b)}$
is the
$(D_y f)_{(a,b)}$
is the
![]() $m\times n$
matrix
$m\times n$
matrix
 $$ \begin{align*}\left (\frac{\partial f_i}{\partial y_t}(a,b)\right )_{ 1\leq i\leq m, 1\leq t\leq n}.\end{align*} $$
$$ \begin{align*}\left (\frac{\partial f_i}{\partial y_t}(a,b)\right )_{ 1\leq i\leq m, 1\leq t\leq n}.\end{align*} $$
Then,
![]() $(Df)_{(a,b)}$
is the
$(Df)_{(a,b)}$
is the
![]() $m\times (r+n)$
-matrix
$m\times (r+n)$
-matrix
For a
![]() $C^1$
map
$C^1$
map
![]() $f:V\to W$
between open subsets of
$f:V\to W$
between open subsets of
![]() $K^n$
and
$K^n$
and
![]() $K^m$
, respectively, we write
$K^m$
, respectively, we write
![]() $Df:V\times K^n\to W\times K^m$
, for the map
$Df:V\times K^n\to W\times K^m$
, for the map
where
![]() $(Df)_a\cdot u=(\sum _{i=1}^n \frac {\partial f_j}{\partial x_i} (a) u_i)_{j=1}^m.$
$(Df)_a\cdot u=(\sum _{i=1}^n \frac {\partial f_j}{\partial x_i} (a) u_i)_{j=1}^m.$
2.1 Definable manifolds and their tangent bundles
Definition 2.1 An
![]() ${\mathcal {L}}$
-definable
${\mathcal {L}}$
-definable
![]() $C^1$
manifold of dimension r, with respect to K, is a topological Hausdorff space M, together with a finite open cover
$C^1$
manifold of dimension r, with respect to K, is a topological Hausdorff space M, together with a finite open cover
![]() $M=\bigcup _{i=1}^n W_i$
, and homeomorphisms
$M=\bigcup _{i=1}^n W_i$
, and homeomorphisms
![]() $\phi _i:V_i\to W_i$
, where
$\phi _i:V_i\to W_i$
, where
![]() $V_i\subseteq K^r$
is a definable open set, such that
$V_i\subseteq K^r$
is a definable open set, such that
![]() $V_{i,j}=\phi _i^{-1}(W_i\cap W_j)$
is a definable open subset of
$V_{i,j}=\phi _i^{-1}(W_i\cap W_j)$
is a definable open subset of
![]() $V_i$
, and each map
$V_i$
, and each map
![]() $\phi _{i.j}=\phi _j^{-1}\circ \phi _i:V_{i,j}\to V_{j,i}$
is a definable
$\phi _{i.j}=\phi _j^{-1}\circ \phi _i:V_{i,j}\to V_{j,i}$
is a definable
![]() $C^1$
-map (between definable open subsets of
$C^1$
-map (between definable open subsets of
![]() $K^r$
).
$K^r$
).
The collection
![]() $\{(V_i,W_i,\phi _i)_{i\in I}\}$
is an atlas for M. We identify the manifold with the quotient of the disjoint union
$\{(V_i,W_i,\phi _i)_{i\in I}\}$
is an atlas for M. We identify the manifold with the quotient of the disjoint union
![]() $\bigsqcup _i V_i$
by the equivalence relation
$\bigsqcup _i V_i$
by the equivalence relation
![]() $a \sim _M b \Leftrightarrow b=\phi _{i,j}(a).$
We say that the manifold is defined over A if the sets and functions in the atlas are all defined over A.
$a \sim _M b \Leftrightarrow b=\phi _{i,j}(a).$
We say that the manifold is defined over A if the sets and functions in the atlas are all defined over A.
If we omit the
![]() $C^1$
requirement from the transition maps, then the manifold is called a definable topological (or
$C^1$
requirement from the transition maps, then the manifold is called a definable topological (or
![]() $C^0$
) manifold.
$C^0$
) manifold.
If
![]() $M, N$
are
$M, N$
are
![]() ${\mathcal {L}}$
-definable
${\mathcal {L}}$
-definable
![]() $C^1$
(or
$C^1$
(or
![]() $C^0$
)-manifolds, then so is
$C^0$
)-manifolds, then so is
![]() $M\times N$
, with the natural atlas.
$M\times N$
, with the natural atlas.
Definition 2.2 For M an
![]() ${\mathcal {L}}$
-definable
${\mathcal {L}}$
-definable
![]() $C^1$
-manifold of dimension r given as above, we let the tangent space of M,
$C^1$
-manifold of dimension r given as above, we let the tangent space of M,
![]() $T(M)$
be the quotient of
$T(M)$
be the quotient of
![]() $\bigsqcup _{i=1}^n V_i\times K^r$
by the equivalence relation, denoted by
$\bigsqcup _{i=1}^n V_i\times K^r$
by the equivalence relation, denoted by
![]() $\sim _{T(M)}$
, given via the maps:
$\sim _{T(M)}$
, given via the maps:
We then write
and denote (equivalence classes of) elements in
![]() $T(M)$
by
$T(M)$
by
![]() $[a,u]$
,
$[a,u]$
,
![]() $a\in \bigsqcup _i V_i$
,
$a\in \bigsqcup _i V_i$
,
![]() $u\in K^r$
.
$u\in K^r$
.
Note that if
![]() $M=U\subseteq K^r$
is a definable open set with the identity atlas, then
$M=U\subseteq K^r$
is a definable open set with the identity atlas, then
![]() ${T(M)=U\times K^r}$
.
${T(M)=U\times K^r}$
.
The following are easy to verify.
Lemma 2.3 Assume that M and N are
![]() ${\mathcal {L}}$
-definable,
${\mathcal {L}}$
-definable,
![]() $C^1$
-manifolds, given by atlases
$C^1$
-manifolds, given by atlases
![]() $(W_i,V_i,\phi _i)_{i\in I}$
and
$(W_i,V_i,\phi _i)_{i\in I}$
and
![]() $(U_j,Z_j,\psi _j)_{j\in J}$
. If
$(U_j,Z_j,\psi _j)_{j\in J}$
. If
![]() $f:M\to N$
is a
$f:M\to N$
is a
![]() $C^1$
-map (read through the charts), then there is a well-defined continuous map
$C^1$
-map (read through the charts), then there is a well-defined continuous map
![]() $Df:T(M)\to T(N)$
satisfying, whenever the elements are in the appropriate
$Df:T(M)\to T(N)$
satisfying, whenever the elements are in the appropriate
![]() $V_i$
and
$V_i$
and
![]() $U_j$
,
$U_j$
,
Proof In fact, the map
![]() $(a,u)\mapsto (f(a),D(\psi _j^{-1}\circ f\circ \phi _i)_{a}\cdot u)$
induces a well-defined map from
$(a,u)\mapsto (f(a),D(\psi _j^{-1}\circ f\circ \phi _i)_{a}\cdot u)$
induces a well-defined map from
![]() $T(M)$
into
$T(M)$
into
![]() $\bigsqcup _{j\in J} U_j\times K^{\dim N}$
. The quotient by
$\bigsqcup _{j\in J} U_j\times K^{\dim N}$
. The quotient by
![]() $\sim _{T(N)}$
gives the desired map.
$\sim _{T(N)}$
gives the desired map.
Lemma 2.4
-
(1) For
 $M,N\ {\mathcal {L}}$
-definable,
$M,N\ {\mathcal {L}}$
-definable,
 $C^1$
-manifolds,
$C^1$
-manifolds,
 $T(M\times N)=T(M)\times T(N)$
.
$T(M\times N)=T(M)\times T(N)$
. -
(2) (Chain rule) For
 $f:M\to N$
and
$f:M\to N$
and
 $h:N\to S$
two
$h:N\to S$
two
 ${\mathcal {L}}$
-definable
${\mathcal {L}}$
-definable
 $C^1$
-maps between
$C^1$
-maps between
 ${\mathcal {L}}$
-definable
${\mathcal {L}}$
-definable
 $C^1$
manifolds,
$C^1$
manifolds,
 $D(h\circ f)=D(h)\circ D(f)$
.
$D(h\circ f)=D(h)\circ D(f)$
.
Summarizing, we have the following lemma.
Lemma 2.5
![]() $(T,D)$
is a functor from the category of definable
$(T,D)$
is a functor from the category of definable
![]() $C^1$
-manifolds to the category of definable
$C^1$
-manifolds to the category of definable
![]() $C^0$
-manifolds. It, moreover, preserves products.
$C^0$
-manifolds. It, moreover, preserves products.
3 Adding a derivation
Let T be a complete, model complete theory of an o-minimal expansion of a real closed field K, in a language
![]() ${\mathcal {L}}$
. The following definition is due to Fornasiero and Kaplan [Reference Fornasiero and Kaplan6].
${\mathcal {L}}$
. The following definition is due to Fornasiero and Kaplan [Reference Fornasiero and Kaplan6].
Definition 3.1 A derivation
![]() $\partial :K\to K$
is called T-compatible if for every
$\partial :K\to K$
is called T-compatible if for every
![]() $\emptyset $
-definable
$\emptyset $
-definable
![]() $C^1$
map
$C^1$
map
![]() $f:U\to K$
, for
$f:U\to K$
, for
![]() $U\subseteq K^m$
open, for all
$U\subseteq K^m$
open, for all
![]() $a\in U$
, we have
$a\in U$
, we have
(Here,
![]() $\partial (a_1,\ldots , a_m)=(\partial a_1,\ldots , \partial a_m)^t$
.)
$\partial (a_1,\ldots , a_m)=(\partial a_1,\ldots , \partial a_m)^t$
.)
Note that if
![]() $a\in dcl(\emptyset )$
and
$a\in dcl(\emptyset )$
and
![]() $\partial $
is T-compatible, then
$\partial $
is T-compatible, then
![]() $\partial (a)=0$
.
$\partial (a)=0$
.
Fornasiero and Kaplan [Reference Fornasiero and Kaplan6] show that the
![]() ${\mathcal {L}}_\partial $
theory
${\mathcal {L}}_\partial $
theory
![]() $T\cup $
“
$T\cup $
“
![]() $\partial $
is a compatible derivation” has a model companion, which we call
$\partial $
is a compatible derivation” has a model companion, which we call
![]() $T_\partial $
. We assume from now on that
$T_\partial $
. We assume from now on that
![]() $\partial $
is a T-compatible derivation on K, and work in models of
$\partial $
is a T-compatible derivation on K, and work in models of
![]() $T_\partial $
. See [Reference Fornasiero and Kaplan6, Proposition 2.8 and Lemma 2.9] for instances where the compatibility condition holds.
$T_\partial $
. See [Reference Fornasiero and Kaplan6, Proposition 2.8 and Lemma 2.9] for instances where the compatibility condition holds.
We observe the following claim.
Claim 3.2 Assume that
![]() $M=\bigsqcup _i V_i/\sim _M$
is a
$M=\bigsqcup _i V_i/\sim _M$
is a
![]() $\emptyset $
-definable manifold. Then, for
$\emptyset $
-definable manifold. Then, for
![]() $a\in M$
,
$a\in M$
,
![]() $\partial a$
is a well-defined element of
$\partial a$
is a well-defined element of
![]() $T(M)_a$
. Namely, if
$T(M)_a$
. Namely, if
![]() $a_i\sim _{M} a_j$
, then
$a_i\sim _{M} a_j$
, then
![]() $(a_i,\partial a_i) \sim _{T(M)}(a_j,\partial a_j)$
.
$(a_i,\partial a_i) \sim _{T(M)}(a_j,\partial a_j)$
.
Proof This is easy to verify, using the compatibility of
![]() $\partial $
.
$\partial $
.
3.1 The definition of
 $f^{\partial }$
on an open set
$f^{\partial }$
on an open set
The following theorem of Fornasiero and Kaplan, which follows easily from their [Reference Fornasiero and Kaplan6, Lemma A.3], plays an important role here: in the Appendix, we prove the analogous result, Proposition A.1, for p-adically closed fields, and the proof could be modified to give an alternative proof in the o-minimal setting as well.
Fact 3.3 Assume that
![]() $g:W\to K^r$
is an
$g:W\to K^r$
is an
![]() ${\mathcal {L}}(\emptyset )$
-definable partial function on some open
${\mathcal {L}}(\emptyset )$
-definable partial function on some open
![]() $W\subseteq K^n\times K^m$
, and
$W\subseteq K^n\times K^m$
, and
![]() $b\in \pi _2(W)\subseteq K^m$
is
$b\in \pi _2(W)\subseteq K^m$
is
![]() $dcl_{{\mathcal {L}}}$
-independent. If
$dcl_{{\mathcal {L}}}$
-independent. If
![]() $g(x,b)$
is a
$g(x,b)$
is a
![]() $C^1$
-map on
$C^1$
-map on
![]() $W^b=\{a\in K^n:(a,b)\in W\}$
, then for every
$W^b=\{a\in K^n:(a,b)\in W\}$
, then for every
![]() $a\in W^b$
, the function g is a
$a\in W^b$
, the function g is a
![]() $C^1$
-function (of all variables) at
$C^1$
-function (of all variables) at
![]() $(a,b)$
.
$(a,b)$
.
As a corollary, one obtains the following.
Fact 3.4 If
![]() $f(x)$
is an
$f(x)$
is an
![]() ${\mathcal {L}}(A)$
-definable
${\mathcal {L}}(A)$
-definable
![]() $C^1$
-function on an open subset of
$C^1$
-function on an open subset of
![]() $K^n$
, then there is a
$K^n$
, then there is a
![]() $dcl_{{\mathcal {L}}(\emptyset )}$
-independent tuple
$dcl_{{\mathcal {L}}(\emptyset )}$
-independent tuple
![]() $b \subseteq A$
, and an
$b \subseteq A$
, and an
![]() ${\mathcal {L}}(\emptyset )$
-definable
${\mathcal {L}}(\emptyset )$
-definable
![]() $C^1$
-function
$C^1$
-function
![]() $g(x,y)$
on an open subset of
$g(x,y)$
on an open subset of
![]() $K^n\times K^{|b|}$
such that
$K^n\times K^{|b|}$
such that
![]() $f(x)=g(x,b)$
.
$f(x)=g(x,b)$
.
Definition 3.5 For
![]() $U\subseteq K^n$
open and
$U\subseteq K^n$
open and
![]() $f:U\to K^r$
an
$f:U\to K^r$
an
![]() ${\mathcal {L}}$
-definable
${\mathcal {L}}$
-definable
![]() $C^1$
-map (possibly over additional parameters), let
$C^1$
-map (possibly over additional parameters), let
Notice that if f is
![]() $\emptyset $
-definable, then
$\emptyset $
-definable, then
![]() $f^\partial (a)=0$
. For the following, see also [Reference Fornasiero and Kaplan6, Lemma 2.12].
$f^\partial (a)=0$
. For the following, see also [Reference Fornasiero and Kaplan6, Lemma 2.12].
Lemma 3.6 If
![]() $f:U\to K^r$
is an
$f:U\to K^r$
is an
![]() ${\mathcal {L}}$
-definable
${\mathcal {L}}$
-definable
![]() $C^1$
map, over a differential field k, then
$C^1$
map, over a differential field k, then
![]() $f^\partial $
is
$f^\partial $
is
![]() ${\mathcal {L}}$
-definable over k, and continuous on U.
${\mathcal {L}}$
-definable over k, and continuous on U.
Proof By Fact 3.4, we may write
![]() $f(x)=g(x,b)$
, for
$f(x)=g(x,b)$
, for
![]() $b\in K^m$
which is
$b\in K^m$
which is
![]() ${\mathcal {L}}(\emptyset )$
-independent, and g which is a
${\mathcal {L}}(\emptyset )$
-independent, and g which is a
![]() $C^1$
map,
$C^1$
map,
![]() ${\mathcal {L}}(\emptyset )$
-definable. By the compatibility of
${\mathcal {L}}(\emptyset )$
-definable. By the compatibility of
![]() $\partial $
,
$\partial $
,
It follows that
![]() $f^\partial (a)=\partial f(a)-(Df)_a\partial a=(D_yg)_{(a,b)}\partial b,$
and since
$f^\partial (a)=\partial f(a)-(Df)_a\partial a=(D_yg)_{(a,b)}\partial b,$
and since
![]() $b\in k$
, then so is
$b\in k$
, then so is
![]() $\partial b$
. Also, because g is a
$\partial b$
. Also, because g is a
![]() $C^1$
-function,
$C^1$
-function,
![]() $f^{\partial }$
is continuous.
$f^{\partial }$
is continuous.
Remark 3.7 When
![]() $p(x)=\sum _m a_m x^m$
is a polynomial over k, then
$p(x)=\sum _m a_m x^m$
is a polynomial over k, then
![]() $p^\partial (x)$
is a polynomial over k of the same degree:
$p^\partial (x)$
is a polynomial over k of the same degree:
For
![]() $a\in K^n$
, we let
$a\in K^n$
, we let
![]() $\nabla (a)=(a,\partial a)$
, and for
$\nabla (a)=(a,\partial a)$
, and for
![]() $r\in \mathbb N$
,
$r\in \mathbb N$
,
![]() $\nabla ^r(a)=(a,\partial a,\ldots , \partial ^r a).$
We also need the following.
$\nabla ^r(a)=(a,\partial a,\ldots , \partial ^r a).$
We also need the following.
Lemma 3.8 Assume that
![]() $k\subseteq K$
is a differential field,
$k\subseteq K$
is a differential field,
![]() $a\in K^m,c\in K^n$
, and
$a\in K^m,c\in K^n$
, and
![]() ${c\in dcl_{{\mathcal {L}}}(k,a)}$
. Then
${c\in dcl_{{\mathcal {L}}}(k,a)}$
. Then
![]() $\nabla (c)\in dcl_{{\mathcal {L}}}(k,\nabla (a))$
. If, in addition, c and a are
$\nabla (c)\in dcl_{{\mathcal {L}}}(k,\nabla (a))$
. If, in addition, c and a are
![]() ${\mathcal {L}}$
-interdefinable over k, then
${\mathcal {L}}$
-interdefinable over k, then
![]() $\nabla (a)$
and
$\nabla (a)$
and
![]() $\nabla (c)$
are
$\nabla (c)$
are
![]() ${\mathcal {L}}$
-interdefinable over k.
${\mathcal {L}}$
-interdefinable over k.
Proof Assume first that a is
![]() ${\mathcal {L}}$
-generic in
${\mathcal {L}}$
-generic in
![]() $K^m$
over k. Then,
$K^m$
over k. Then,
![]() $c=f(a)$
for f an
$c=f(a)$
for f an
![]() ${\mathcal {L}}$
-definable over k and
${\mathcal {L}}$
-definable over k and
![]() $C^1$
at a. We have
$C^1$
at a. We have
![]() $\partial f(a)=(Df)_a \partial a+f^\partial (a),$
where, by Lemma 3.6,
$\partial f(a)=(Df)_a \partial a+f^\partial (a),$
where, by Lemma 3.6,
![]() $f^\partial (x)$
is
$f^\partial (x)$
is
![]() ${\mathcal {L}}$
-definable over k. So, if we let
${\mathcal {L}}$
-definable over k. So, if we let
![]() $h(x,u)=(f(x),(Df)_x u+f^{\partial }(x))$
, then
$h(x,u)=(f(x),(Df)_x u+f^{\partial }(x))$
, then
![]() $h(\nabla (a))=\nabla (c)$
, so
$h(\nabla (a))=\nabla (c)$
, so
![]() $\nabla (c)\in dcl_{{\mathcal {L}}}(k,a)$
.
$\nabla (c)\in dcl_{{\mathcal {L}}}(k,a)$
.
Given a general
![]() $a\in K^m$
, we can write it, up to permutation of coordinates, as
$a\in K^m$
, we can write it, up to permutation of coordinates, as
![]() $(a_1,a_2)$
where
$(a_1,a_2)$
where
![]() $a_1\in K^{m_1}$
is
$a_1\in K^{m_1}$
is
![]() ${\mathcal {L}}$
-generic over k and
${\mathcal {L}}$
-generic over k and
![]() $a_2\in dcl_{{\mathcal {L}}}(a_1)$
. Then
$a_2\in dcl_{{\mathcal {L}}}(a_1)$
. Then
![]() $c\in dcl_{{\mathcal {L}}}(k,a_1)$
, so by what we saw,
$c\in dcl_{{\mathcal {L}}}(k,a_1)$
, so by what we saw,
![]() $\nabla (c)\in dcl_{{\mathcal {L}}}(k,\nabla (a_1))\subseteq dcl_{{\mathcal {L}}}(k,\nabla (a))$
.
$\nabla (c)\in dcl_{{\mathcal {L}}}(k,\nabla (a_1))\subseteq dcl_{{\mathcal {L}}}(k,\nabla (a))$
.
Finally, it clearly follows that if a and c are
![]() ${\mathcal {L}}$
-interdefinable over k, then so are
${\mathcal {L}}$
-interdefinable over k, then so are
![]() $\nabla (a)$
and
$\nabla (a)$
and
![]() $\nabla (c)$
.
$\nabla (c)$
.
3.2 Prolongation of functions on open sets
Here and below, we make use of Marker’s account [Reference Marker14] of prolongations in the algebraic setting.
Definition 3.9 For
![]() $U\subseteq K^r$
open and
$U\subseteq K^r$
open and
![]() $f:U\to K^n$
an
$f:U\to K^n$
an
![]() ${\mathcal {L}}$
-definable
${\mathcal {L}}$
-definable
![]() $C^1$
-map, we let
$C^1$
-map, we let
![]() $\tau (f):U\times K^r\to K^n\times K^n$
be defined as
$\tau (f):U\times K^r\to K^n\times K^n$
be defined as
Using Lemma 3.6 (the
![]() ${\mathcal {L}}$
-definability of
${\mathcal {L}}$
-definability of
![]() $f^\partial $
) and the
$f^\partial $
) and the
![]() ${\mathcal {L}}$
-definability of
${\mathcal {L}}$
-definability of
![]() $Df$
, we have the following lemma.
$Df$
, we have the following lemma.
Lemma 3.10 If f is a
![]() $C^1$
-map,
$C^1$
-map,
![]() ${\mathcal {L}}$
-definable over a differential field k, then
${\mathcal {L}}$
-definable over a differential field k, then
![]() $\tau (f)$
is continuous and
$\tau (f)$
is continuous and
![]() ${\mathcal {L}}$
-definable over the same k.
${\mathcal {L}}$
-definable over the same k.
Using the second equality in the definition of
![]() $\tau (f)$
and the chain rule for D, we immediately obtain the following lemma.
$\tau (f)$
and the chain rule for D, we immediately obtain the following lemma.
Lemma 3.11 If
![]() $f:U\to V$
and
$f:U\to V$
and
![]() $h:V\to W$
are definable
$h:V\to W$
are definable
![]() $C^1$
-functions on open sets, then
$C^1$
-functions on open sets, then
3.3 The definition of
 $\tau (M)$
and
$\tau (M)$
and
 $\tau (f)$
for definable manifolds
$\tau (f)$
for definable manifolds
Definition 3.12 Assume that
![]() $M=\bigsqcup _i V_i/\sim _M$
is an
$M=\bigsqcup _i V_i/\sim _M$
is an
![]() ${\mathcal {L}}$
-definable
${\mathcal {L}}$
-definable
![]() $C^1$
-manifold of dimension n. Then the prolongation of M is defined as
$C^1$
-manifold of dimension n. Then the prolongation of M is defined as
where
![]() $(a_i,u)\sim _{\tau (M)}(a_j,v)$
if
$(a_i,u)\sim _{\tau (M)}(a_j,v)$
if
![]() $\tau (\phi _{i,j})(a_i,u)=(a_j,v)$
.
$\tau (\phi _{i,j})(a_i,u)=(a_j,v)$
.
By Lemma 3.10,
![]() $\tau (M)$
is an
$\tau (M)$
is an
![]() ${\mathcal {L}}$
-definable
${\mathcal {L}}$
-definable
![]() $C^0$
-manifold.
$C^0$
-manifold.
The following is easy to verify.
Lemma 3.13 Assume that
![]() $M=\bigsqcup _i V_i/\sim _M$
is an
$M=\bigsqcup _i V_i/\sim _M$
is an
![]() ${\mathcal {L}}$
-definable
${\mathcal {L}}$
-definable
![]() $C^1$
-manifold. Then
$C^1$
-manifold. Then
In particular, the map
induces a well-defined
![]() ${\mathcal {L}}_{\partial }$
-definable bijection over
${\mathcal {L}}_{\partial }$
-definable bijection over
![]() $M$
, between
$M$
, between
![]() $T(M)$
and
$T(M)$
and
![]() $\tau (M)$
.
$\tau (M)$
.
Using the above lemma, we see that for
![]() $a\in M$
, the element
$a\in M$
, the element
![]() $(a,\partial a)\in \tau (M)$
is well defined (e.g., as
$(a,\partial a)\in \tau (M)$
is well defined (e.g., as
![]() $\sigma _M(a,0)$
). We thus have a well-defined map
$\sigma _M(a,0)$
). We thus have a well-defined map
![]() $\nabla :M\to \tau (M)$
, given in coordinates by
$\nabla :M\to \tau (M)$
, given in coordinates by
![]() $\nabla _M(a)=(a,\partial a)$
.
$\nabla _M(a)=(a,\partial a)$
.
Definition 3.14 Assume that M and N are
![]() ${\mathcal {L}}$
-definable
${\mathcal {L}}$
-definable
![]() $C^1$
-manifolds,
$C^1$
-manifolds,
![]() $f:M\to N$
an
$f:M\to N$
an
![]() ${\mathcal {L}}$
-definable
${\mathcal {L}}$
-definable
![]() $C^1$
map. Then the prolongation of f,
$C^1$
map. Then the prolongation of f,
![]() $\tau (f):\tau (M)\to \tau (N)$
, is defined by
$\tau (f):\tau (M)\to \tau (N)$
, is defined by
The following is easy to verify.
Lemma 3.15 Assume that M and N as above are given via the atlases
![]() $\{(V_i,W_i,\phi _i)_{i\in I}\}$
and
$\{(V_i,W_i,\phi _i)_{i\in I}\}$
and
![]() $\{(U_j,Z_j,\psi _j)\}$
, respectively, with
$\{(U_j,Z_j,\psi _j)\}$
, respectively, with
![]() $\dim M=r$
and
$\dim M=r$
and
![]() $\dim N=n$
. If
$\dim N=n$
. If
![]() $f:M\to N$
is an
$f:M\to N$
is an
![]() ${\mathcal {L}}$
-definable
${\mathcal {L}}$
-definable
![]() $C^1$
-map, then, for
$C^1$
-map, then, for
![]() $(a,u)\in V_i\times K^r$
, we have
$(a,u)\in V_i\times K^r$
, we have
Lemma 3.16 Let
![]() $M,N$
be
$M,N$
be
![]() ${\mathcal {L}}$
-definable
${\mathcal {L}}$
-definable
![]() $C^1$
-manifolds defined over a differential field k.
$C^1$
-manifolds defined over a differential field k.
-
(1) If
 $f:M\to N$
is
$f:M\to N$
is
 ${\mathcal {L}}$
-definable over k, then so is
${\mathcal {L}}$
-definable over k, then so is
 $\tau (f):\tau (M)\to \tau (N)$
, and
$\tau (f):\tau (M)\to \tau (N)$
, and
 $\tau (f)$
is continuous.
$\tau (f)$
is continuous. -
(2) If
 $f:M\to N$
and
$f:M\to N$
and
 $h:N\to S$
are
$h:N\to S$
are
 ${\mathcal {L}}$
-definable
${\mathcal {L}}$
-definable
 $C^1$
maps between
$C^1$
maps between
 ${\mathcal {L}}$
-definable
${\mathcal {L}}$
-definable
 $C^1$
-manifolds, then
$C^1$
-manifolds, then
 $\tau (h\circ f)=\tau (h)\circ \tau (f)$
.
$\tau (h\circ f)=\tau (h)\circ \tau (f)$
. -
(3) We have
 $\tau (M\times N)=\tau (M)\times \tau (N)$
. Moreover, if
$\tau (M\times N)=\tau (M)\times \tau (N)$
. Moreover, if
 $\pi _1:M\times N\to N$
and
$\pi _1:M\times N\to N$
and
 $\pi _1:\tau (M)\times \tau (N)\to \tau (M)$
are the projection maps on the first coordinates, then
$\pi _1:\tau (M)\times \tau (N)\to \tau (M)$
are the projection maps on the first coordinates, then
 $\tau (\pi _1)=\pi _1\circ \tau .$
$\tau (\pi _1)=\pi _1\circ \tau .$
-
(4) We have
 $\nabla _N \circ f=\tau (f)\circ \nabla _M$
.
$\nabla _N \circ f=\tau (f)\circ \nabla _M$
.
Proof (1) By Lemma 3.15, the result reduces to the
![]() ${\mathcal {L}}$
-definability of each
${\mathcal {L}}$
-definability of each
![]() $\tau (\psi _j^{-1}\circ f\circ \phi _i)$
, and therefore follows from Lemma 3.6. (2) follows from Lemma 3.11. (3) and (4) are easy to verify.
$\tau (\psi _j^{-1}\circ f\circ \phi _i)$
, and therefore follows from Lemma 3.6. (2) follows from Lemma 3.11. (3) and (4) are easy to verify.
As a corollary, we have the following lemma.
Lemma 3.17
![]() $\tau $
is a functor from the category of definable
$\tau $
is a functor from the category of definable
![]() $C^1$
-manifolds to definable
$C^1$
-manifolds to definable
![]() $C^0$
manifolds, which moreover preserves products.
$C^0$
manifolds, which moreover preserves products.
4
 ${\mathcal {L}}_\partial $
-definable groups
${\mathcal {L}}_\partial $
-definable groups
4.1 Prolongation of
 ${\mathcal {L}}$
-definable groups, D-groups, and Nash D-groups
${\mathcal {L}}$
-definable groups, D-groups, and Nash D-groups
Let G be an
![]() ${\mathcal {L}}$
-definable group of dimension m. By [Reference Pillay16], it admits the structure of an
${\mathcal {L}}$
-definable group of dimension m. By [Reference Pillay16], it admits the structure of an
![]() ${\mathcal {L}}$
-definable
${\mathcal {L}}$
-definable
![]() $C^0$
-manifold. Since we shall be using the particular construction, in its
$C^0$
-manifold. Since we shall be using the particular construction, in its
![]() $C^1$
-version, we repeat the details below for future use (see [Reference Pillay16, Lemmas 2.4 and Proposition 2.5]).
$C^1$
-version, we repeat the details below for future use (see [Reference Pillay16, Lemmas 2.4 and Proposition 2.5]).
Fact 4.1 There exist a group topology t on G, a large
![]() ${\mathcal {L}}$
-definable set
${\mathcal {L}}$
-definable set
![]() $W\subseteq G$
, a definable open
$W\subseteq G$
, a definable open
![]() $V\subseteq K^m$
, and an
$V\subseteq K^m$
, and an
![]() ${\mathcal {L}}$
-definable homeomorphism
${\mathcal {L}}$
-definable homeomorphism
![]() $\sigma $
from V (with the
$\sigma $
from V (with the
![]() $K^m$
-topology) and W (with the t-topology), and there are
$K^m$
-topology) and W (with the t-topology), and there are
![]() $g_1,\ldots , g_k\in G$
, such that:
$g_1,\ldots , g_k\in G$
, such that:
(i)
![]() $G=\bigcup _j g_j W$
.
$G=\bigcup _j g_j W$
.
(ii) The maps
![]() $\phi _i: V\to g_iW: x\mapsto g_i\sigma (x)$
endow
$\phi _i: V\to g_iW: x\mapsto g_i\sigma (x)$
endow
![]() $(G,t)$
with a definable
$(G,t)$
with a definable
![]() $C^1$
-atlas.
$C^1$
-atlas.
(iii) The group G is a
![]() $C^1$
-group with respect to this atlas, namely the group operations of G are
$C^1$
-group with respect to this atlas, namely the group operations of G are
![]() $C^1$
maps.
$C^1$
maps.
To be precise, [Reference Pillay16, Proposition 2.5] states the result in the
![]() $C^0$
category. However, as is commented in [Reference Pillay16, Remark 2.6], if the underlying o-minimal structure is the field
$C^0$
category. However, as is commented in [Reference Pillay16, Remark 2.6], if the underlying o-minimal structure is the field
![]() $(\mathbb R,<,+,\cdot )$
, then one can obtain an analytic atlas for G, making it an analytic group. If we work, as we do here, in an o-minimal structure over an arbitrary real closed field, where definable functions are piecewise
$(\mathbb R,<,+,\cdot )$
, then one can obtain an analytic atlas for G, making it an analytic group. If we work, as we do here, in an o-minimal structure over an arbitrary real closed field, where definable functions are piecewise
![]() $C^1$
[Reference van den Dries23, Theorem 6.3.2], then exactly the same proof would yield the above
$C^1$
[Reference van den Dries23, Theorem 6.3.2], then exactly the same proof would yield the above
![]() $C^1$
-atlas, making G a
$C^1$
-atlas, making G a
![]() $C^1$
-group. Moreover, every other definable
$C^1$
-group. Moreover, every other definable
![]() $C^1$
-atlas on G which makes it into a
$C^1$
-atlas on G which makes it into a
![]() $C^1$
group yields the same
$C^1$
group yields the same
![]() $C^1$
-structure, namely the identity map is a diffeomorphism of the two (this follows from the fact that definable functions are generically
$C^1$
-structure, namely the identity map is a diffeomorphism of the two (this follows from the fact that definable functions are generically
![]() $C^1$
). In addition, if G was definable over A, then since the notion of a
$C^1$
). In addition, if G was definable over A, then since the notion of a
![]() $C^1$
-atlas is first-order, one can obtain a corresponding
$C^1$
-atlas is first-order, one can obtain a corresponding
![]() $C^1$
-atlas for G which is also defined over A.
$C^1$
-atlas for G which is also defined over A.
Remark 4.2 The result above, from [Reference Pillay16], has already been used in several other settings (e.g. [Reference Pillay17]). As we shall be using it again in the p-adic setting, we point out that Fact 4.1 holds (with the exact same proof) under the following assumptions: the group
![]() $G\subseteq K^n$
, is definable is an
$G\subseteq K^n$
, is definable is an
![]() ${\mathcal {L}}$
-expansion of a topological field K (namely, a field with a definable basis for a Hausdorff, non-discrete, field topology), which is a geometric structure, and in addition admits a
${\mathcal {L}}$
-expansion of a topological field K (namely, a field with a definable basis for a Hausdorff, non-discrete, field topology), which is a geometric structure, and in addition admits a
![]() $C^1$
-cell decomposition.
$C^1$
-cell decomposition.
From now on, one we endow every
![]() ${\mathcal {L}}$
-definable group G with its canonical
${\mathcal {L}}$
-definable group G with its canonical
![]() $C^1$
-structure.
$C^1$
-structure.
By purely categorical reasons, using Lemmas 2.5 and 3.17, we have (see [Reference Marker14, Section 2] for the same construction in algebraic groups) the following lemma.
Lemma 4.3 Let G be a definable group, endowed with its canonical
![]() $C^1$
-structure, and let
$C^1$
-structure, and let
![]() $m:G\times G\to G$
be the group product. Then
$m:G\times G\to G$
be the group product. Then
are
![]() ${\mathcal {L}}$
-definable
${\mathcal {L}}$
-definable
![]() $C^0$
-groups (namely, topological groups with respect to an
$C^0$
-groups (namely, topological groups with respect to an
![]() ${\mathcal {L}}$
-definable
${\mathcal {L}}$
-definable
![]() $C^0$
-atlas)), and the function
$C^0$
-atlas)), and the function
![]() $[a,u]\mapsto a$
is in both cases an
$[a,u]\mapsto a$
is in both cases an
![]() ${\mathcal {L}}$
-definable group homomorphism from
${\mathcal {L}}$
-definable group homomorphism from
![]() $T(G)$
and
$T(G)$
and
![]() $\tau (G)$
onto G.
$\tau (G)$
onto G.
The map
![]() $a\mapsto [a,0]: G\to T(G)$
is an
$a\mapsto [a,0]: G\to T(G)$
is an
![]() ${\mathcal {L}}$
-definable group section and
${\mathcal {L}}$
-definable group section and
![]() $\nabla _G:G\to \tau (G)$
is an
$\nabla _G:G\to \tau (G)$
is an
![]() ${\mathcal {L}}_{\partial }$
-definable group section.
${\mathcal {L}}_{\partial }$
-definable group section.
Definition 4.4 Assume that G is an
![]() ${\mathcal {L}}$
-definable group, and
${\mathcal {L}}$
-definable group, and
![]() $s:G\to \tau (G)$
is an
$s:G\to \tau (G)$
is an
![]() ${\mathcal {L}}$
-definable group section. Then the pair
${\mathcal {L}}$
-definable group section. Then the pair
![]() $(G,s)$
is called an
$(G,s)$
is called an
![]() ${\mathcal {L}}$
-definable D-group.
${\mathcal {L}}$
-definable D-group.
Remark 4.5 When
![]() $T=RCF$
is the theory of real closed fields, every definable group admits the structure of a Nash group with respect to K. Namely, the underlying manifold and group operations are semialgebraic over K and either real analytic, when
$T=RCF$
is the theory of real closed fields, every definable group admits the structure of a Nash group with respect to K. Namely, the underlying manifold and group operations are semialgebraic over K and either real analytic, when
![]() $K=\mathbb R$
, or
$K=\mathbb R$
, or
![]() $C^\infty $
in general (see discussion in [Reference Hrushovski and Pillay10], based on [Reference Bochnak, Coste and Roy1]). In this case, every definable homomorphism between such groups is a Nash map; thus,
$C^\infty $
in general (see discussion in [Reference Hrushovski and Pillay10], based on [Reference Bochnak, Coste and Roy1]). In this case, every definable homomorphism between such groups is a Nash map; thus,
![]() $\pi :T(G)\to G$
and
$\pi :T(G)\to G$
and
![]() $\pi :\tau (G)\to G$
are Nash maps, and an
$\pi :\tau (G)\to G$
are Nash maps, and an
![]() ${\mathcal {L}}$
-definable section
${\mathcal {L}}$
-definable section
![]() $s:G\to \tau (G)$
is a Nash map. We call a D-group
$s:G\to \tau (G)$
is a Nash map. We call a D-group
![]() $(G,s)$
in this case a Nash D-group.
$(G,s)$
in this case a Nash D-group.
Our goal is to prove the following theorem.
Theorem 4.6 Let
![]() $T_\partial $
be the model companion of a complete, model complete, o-minimal theory T, with a T-compatible derivation
$T_\partial $
be the model companion of a complete, model complete, o-minimal theory T, with a T-compatible derivation
![]() $\partial $
. Assume that
$\partial $
. Assume that
![]() $\Gamma $
is an
$\Gamma $
is an
![]() ${\mathcal {L}}_{\partial }$
-definable group of finite
${\mathcal {L}}_{\partial }$
-definable group of finite
![]() ${\mathcal {L}}_\partial $
-dimension. Then there exists an
${\mathcal {L}}_\partial $
-dimension. Then there exists an
![]() ${\mathcal {L}}$
-definable D-group
${\mathcal {L}}$
-definable D-group
![]() $(G,s)$
and an
$(G,s)$
and an
![]() ${\mathcal {L}}_\partial $
-definable group embedding
${\mathcal {L}}_\partial $
-definable group embedding
![]() $\Gamma \to G$
whose image is
$\Gamma \to G$
whose image is
We first recall our result [Reference Peterzil, Pillay and Point15, Theorem 6.8]. We shall be using the following version.
Theorem 4.7 If
![]() $\Gamma $
is a finite-dimensional
$\Gamma $
is a finite-dimensional
![]() ${\mathcal {L}}_\partial $
-defined group in a model of
${\mathcal {L}}_\partial $
-defined group in a model of
![]() $T_\partial $
, then it can be
$T_\partial $
, then it can be
![]() ${\mathcal {L}}_{\partial }$
-definably embedded in an
${\mathcal {L}}_{\partial }$
-definably embedded in an
![]() ${\mathcal {L}}$
-definable group
${\mathcal {L}}$
-definable group
![]() $G\subseteq K^n$
such that:
$G\subseteq K^n$
such that:
(i) Every
![]() ${\mathcal {L}}$
-generic type
${\mathcal {L}}$
-generic type
![]() $p\vdash G$
is realized by some
$p\vdash G$
is realized by some
![]() $\gamma \in \Gamma $
.
$\gamma \in \Gamma $
.
(ii) There are
![]() ${\mathcal {L}}$
-definable sets
${\mathcal {L}}$
-definable sets
![]() $X_1,\ldots , X_r\subseteq G$
,
$X_1,\ldots , X_r\subseteq G$
,
![]() $G=\bigcup _{i=1}^r X_i$
, and
$G=\bigcup _{i=1}^r X_i$
, and
![]() ${\mathcal {L}}$
-definable functions
${\mathcal {L}}$
-definable functions
![]() $s_i:X_i\to K^n$
such that for each
$s_i:X_i\to K^n$
such that for each
![]() ${\mathcal {L}}$
-generic
${\mathcal {L}}$
-generic
![]() $a\in X_i$
,
$a\in X_i$
,
![]() $a\in \Gamma $
iff
$a\in \Gamma $
iff
![]() $\partial a=s_i(a).$
(Recall that for
$\partial a=s_i(a).$
(Recall that for
![]() $a=(a_1,\ldots , a_n)$
,
$a=(a_1,\ldots , a_n)$
,
![]() $\partial a=(\partial a_1,\ldots , \partial a_n)$
.
$\partial a=(\partial a_1,\ldots , \partial a_n)$
.
Note that as a corollary of above we may obtain
![]() $X^{\prime }_1,\ldots , X^{\prime }_k\subseteq G$
pairwise disjoint, all of the same dimension as
$X^{\prime }_1,\ldots , X^{\prime }_k\subseteq G$
pairwise disjoint, all of the same dimension as
![]() $\dim G$
, satisfying (ii), but instead of
$\dim G$
, satisfying (ii), but instead of
![]() $G=\bigcup X^{\prime }_i$
we have
$G=\bigcup X^{\prime }_i$
we have
![]() $\dim (G\setminus \bigcup X_i')<\dim G$
. Indeed, we replace the original
$\dim (G\setminus \bigcup X_i')<\dim G$
. Indeed, we replace the original
![]() $X_i$
by
$X_i$
by
![]() $X_i'=X_i\setminus \bigcup _{j<i} X_j$
and remove all
$X_i'=X_i\setminus \bigcup _{j<i} X_j$
and remove all
![]() $X_i'$
whose dimension is smaller than
$X_i'$
whose dimension is smaller than
![]() $\dim G$
.
$\dim G$
.
In fact, we shall prove a more precise version of Theorem 4.6.
Theorem Assume that
![]() $\Gamma $
and G satisfy (i) and (ii) of Theorem 4.7. If we endow G with its
$\Gamma $
and G satisfy (i) and (ii) of Theorem 4.7. If we endow G with its
![]() $C^1$
-structure, then there exists an
$C^1$
-structure, then there exists an
![]() ${\mathcal {L}}$
-definable
${\mathcal {L}}$
-definable
![]() $s:G\to \tau (G)$
, such that
$s:G\to \tau (G)$
, such that
![]() $\Gamma =(G, s)^\partial $
, where
$\Gamma =(G, s)^\partial $
, where
![]() $(G, s)^\partial =\{g\in G: s(g)=\nabla (g)\}.$
$(G, s)^\partial =\{g\in G: s(g)=\nabla (g)\}.$
We first prove a general fact about groups in geometric structures.
Proposition 4.8 Let G be a definable group in a geometric structure, and let
![]() $S\subseteq G$
be a definable subset. Assume that for every generic pair
$S\subseteq G$
be a definable subset. Assume that for every generic pair
![]() $(a,b)\in S\times S$
, we have
$(a,b)\in S\times S$
, we have
![]() $a\cdot b\in S$
and for every generic
$a\cdot b\in S$
and for every generic
![]() $a\in S$
we have
$a\in S$
we have
![]() $a^{-1}\in S$
.
$a^{-1}\in S$
.
Then there is a definable
![]() $S_0\subseteq S$
such that
$S_0\subseteq S$
such that
![]() $S_0\cdot S_0$
is a subgroup of G and
$S_0\cdot S_0$
is a subgroup of G and
![]() $S_0$
is a large subset of both S and
$S_0$
is a large subset of both S and
![]() $S_0\cdot S_0$
.
$S_0\cdot S_0$
.
Proof We let
By definability of dimension in geometric structures,
![]() $S_1$
is definable. By our assumptions,
$S_1$
is definable. By our assumptions,
![]() $S_1$
contains all generic elements of S; thus, by our assumptions,
$S_1$
contains all generic elements of S; thus, by our assumptions,
![]() $S_0:=S_1\cap S_1^{-1}$
is also large in S. We claim that
$S_0:=S_1\cap S_1^{-1}$
is also large in S. We claim that
![]() $S_0\cdot S_0$
is a subgroup of G.
$S_0\cdot S_0$
is a subgroup of G.
We need to prove that for every
![]() $a,b,c,d\in S_0$
, we have
$a,b,c,d\in S_0$
, we have
![]() $a b c^{-1} d^{-1}\in S_0\cdot S_0$
. We fix
$a b c^{-1} d^{-1}\in S_0\cdot S_0$
. We fix
![]() $g\in S$
generic over
$g\in S$
generic over
![]() $a,b,c,d$
, and consider
$a,b,c,d$
, and consider
Since
![]() $b\in S_0$
, the set
$b\in S_0$
, the set
![]() $\{t\in S: bt\in S\}$
is large in S, defined over b, and therefore contains g. Thus,
$\{t\in S: bt\in S\}$
is large in S, defined over b, and therefore contains g. Thus,
![]() $bg$
is in S and by our choice, it is in fact generic in S over
$bg$
is in S and by our choice, it is in fact generic in S over
![]() $a,c,d$
, so in particular belongs to
$a,c,d$
, so in particular belongs to
![]() $S_0$
. Thus,
$S_0$
. Thus,
![]() $a(bg)\in S$
, and again generic there over
$a(bg)\in S$
, and again generic there over
![]() $c,d$
, so belongs to
$c,d$
, so belongs to
![]() $S_0$
. Similarly,
$S_0$
. Similarly,
![]() $g^{-1}c^{-1}d^{-1}\in S_0$
, so
$g^{-1}c^{-1}d^{-1}\in S_0$
, so
![]() $abc^{-1}d^{-1}\in S_0\cdot S_0$
. Let
$abc^{-1}d^{-1}\in S_0\cdot S_0$
. Let
![]() $H:=S_0\cdot S_0$
.
$H:=S_0\cdot S_0$
.
To see that
![]() $S_0$
is a large subset of H, we fix
$S_0$
is a large subset of H, we fix
![]() $g\in S_0$
and
$g\in S_0$
and
![]() $h\in S$
generic over g (so
$h\in S$
generic over g (so
![]() $h\in S_0$
). Then
$h\in S_0$
). Then
![]() $g h, gh^{-1}\in S$
and generic there so in
$g h, gh^{-1}\in S$
and generic there so in
![]() $S_0$
. It follows that
$S_0$
. It follows that
![]() $g\in S_0\cdot S_0$
and
$g\in S_0\cdot S_0$
and
![]() $h\in S_0^{-1}\cdot S_0=S_0\cdot S_0$
.
$h\in S_0^{-1}\cdot S_0=S_0\cdot S_0$
.
Hence,
![]() $S_0\subseteq H$
and every generic
$S_0\subseteq H$
and every generic
![]() $h\in S$
over g is in H, so
$h\in S$
over g is in H, so
![]() $S_0$
is large in H.
$S_0$
is large in H.
We are now ready to prove Theorem 4.6.
We first apply Theorem 4.7 and the subsequent corollary and deduce the existence of pairwise disjoint
![]() ${\mathcal {L}}$
-definable
${\mathcal {L}}$
-definable
![]() $X_1,\ldots , X_r\subseteq G\subseteq K^n$
, each of dimension equal to
$X_1,\ldots , X_r\subseteq G\subseteq K^n$
, each of dimension equal to
![]() $m=\dim G$
, such that
$m=\dim G$
, such that
![]() $X=\bigsqcup _j X_j$
is a large subset of G and on each j, we have an
$X=\bigsqcup _j X_j$
is a large subset of G and on each j, we have an
![]() ${\mathcal {L}}$
-definable
${\mathcal {L}}$
-definable
![]() $s_j:X_j\to K^n$
, such that for g generic in
$s_j:X_j\to K^n$
, such that for g generic in
![]() $X_j$
, we have
$X_j$
, we have
![]() $g\in \Gamma \Leftrightarrow \partial g=s_j(g)$
. We let
$g\in \Gamma \Leftrightarrow \partial g=s_j(g)$
. We let
![]() $s:X \to K^n$
be the union of the
$s:X \to K^n$
be the union of the
![]() $s_j$
’s.
$s_j$
’s.
Next, we apply Fact 4.1, and fix an
![]() ${\mathcal {L}}$
-definable large
${\mathcal {L}}$
-definable large
![]() $W\subseteq G$
,
$W\subseteq G$
,
![]() $V\subseteq K^m$
open,
$V\subseteq K^m$
open,
![]() $\sigma :V\to W$
a homeomorphism, and
$\sigma :V\to W$
a homeomorphism, and
![]() $g_1,\ldots , g_k\in G$
, such that the maps
$g_1,\ldots , g_k\in G$
, such that the maps
![]() $\phi _i: V\to g_iW: x\mapsto g_i\sigma (x)$
endow G with a definable
$\phi _i: V\to g_iW: x\mapsto g_i\sigma (x)$
endow G with a definable
![]() $C^1$
-manifold structure, and make G into a
$C^1$
-manifold structure, and make G into a
![]() $C^1$
-group.
$C^1$
-group.
By intersecting W with the relative interior of X in G, we may assume that
![]() $W=X$
.
$W=X$
.
Claim 4.9 There exists an
![]() ${\mathcal {L}}$
-definable
${\mathcal {L}}$
-definable
![]() $\hat s:V\to K^m$
, such that for every
$\hat s:V\to K^m$
, such that for every
![]() ${\mathcal {L}}$
-generic
${\mathcal {L}}$
-generic
![]() $a\in V$
,
$a\in V$
,
![]() $\hat s(a)=\partial a \Leftrightarrow s(\sigma (a))=\partial \sigma (a)$
.
$\hat s(a)=\partial a \Leftrightarrow s(\sigma (a))=\partial \sigma (a)$
.
Proof Every
![]() $a\in V$
is
$a\in V$
is
![]() ${\mathcal {L}}$
-interdefinable with
${\mathcal {L}}$
-interdefinable with
![]() $\sigma (a)$
, so by Lemma 3.8,
$\sigma (a)$
, so by Lemma 3.8,
![]() $\nabla (a)$
and
$\nabla (a)$
and
![]() $\nabla (\sigma (a))$
are
$\nabla (\sigma (a))$
are
![]() ${\mathcal {L}}$
-interdefinable over k. By compactness, there exists an
${\mathcal {L}}$
-interdefinable over k. By compactness, there exists an
![]() ${\mathcal {L}}$
-definable (partial) bijection
${\mathcal {L}}$
-definable (partial) bijection
![]() $h:W\times K^n\to V\times K^m$
, such that for each generic
$h:W\times K^n\to V\times K^m$
, such that for each generic
![]() $a\in V$
,
$a\in V$
,
![]() $h(\nabla (\sigma a))=\nabla (a)$
. Let
$h(\nabla (\sigma a))=\nabla (a)$
. Let
where
![]() $\pi _2:V\times K^n\to K^n$
is the projection onto the second coordinate.
$\pi _2:V\times K^n\to K^n$
is the projection onto the second coordinate.
Now, if
![]() $s(\sigma (a))=\partial (a)$
, then
$s(\sigma (a))=\partial (a)$
, then
![]() $(\sigma (a),s(\sigma (a)))=\nabla (\sigma (a))$
, so
$(\sigma (a),s(\sigma (a)))=\nabla (\sigma (a))$
, so
The converse follows from the invertibility of h.
Going back to G, we now endow G with a finite
![]() $C^1$
-atlas
$C^1$
-atlas
![]() $(V_i,g_iW,\phi _i)_{i\in I}$
, where
$(V_i,g_iW,\phi _i)_{i\in I}$
, where
![]() $V_i=V$
for all i, and identify G with
$V_i=V$
for all i, and identify G with
![]() $\bigsqcup V_i/\sim _M$
. We also identify
$\bigsqcup V_i/\sim _M$
. We also identify
![]() $\Gamma $
with the group
$\Gamma $
with the group
![]() $\bigsqcup \phi _i^{-1}(\Gamma \cap g_iW)/\sim _M$
. Notice that each
$\bigsqcup \phi _i^{-1}(\Gamma \cap g_iW)/\sim _M$
. Notice that each
![]() $g_iW/\sim _M$
is large in G, and by Claim 4.9, there is an
$g_iW/\sim _M$
is large in G, and by Claim 4.9, there is an
![]() ${\mathcal {L}}$
-definable
${\mathcal {L}}$
-definable
![]() $\hat s:V\to K^m$
such that, for generic
$\hat s:V\to K^m$
such that, for generic
![]() $a\in V$
,
$a\in V$
,
![]() $\hat s(a) =\partial a$
if and only if
$\hat s(a) =\partial a$
if and only if
![]() $s(\sigma (a))=\partial \sigma (a)$
. Thus, by our assumption, for every generic
$s(\sigma (a))=\partial \sigma (a)$
. Thus, by our assumption, for every generic
![]() $g\in G$
,
$g\in G$
,
![]() $g\in \Gamma \Leftrightarrow \hat s(g)=\partial g$
. For simplicity, from now on, we use s instead of
$g\in \Gamma \Leftrightarrow \hat s(g)=\partial g$
. For simplicity, from now on, we use s instead of
![]() $\hat s$
and let
$\hat s$
and let
![]() $X=dom (s)$
, an
$X=dom (s)$
, an
![]() ${\mathcal {L}}$
-definable large subset of G.
${\mathcal {L}}$
-definable large subset of G.
Consider the
![]() ${\mathcal {L}}$
-definable
${\mathcal {L}}$
-definable
![]() $C^1$
-group
$C^1$
-group
![]() $\tau (G)$
as before, and the associated
$\tau (G)$
as before, and the associated
![]() ${\mathcal {L}}$
-definable homomorphism
${\mathcal {L}}$
-definable homomorphism
![]() $\pi :\tau (G)\to G$
, together with an
$\pi :\tau (G)\to G$
, together with an
![]() ${\mathcal {L}}_\partial $
-definable group section
${\mathcal {L}}_\partial $
-definable group section
![]() $\nabla _G:G\to \tau (G)$
. The map s can be replaced by
$\nabla _G:G\to \tau (G)$
. The map s can be replaced by
![]() $x\mapsto (x,s(x))$
, so we may think of it as a function from X into
$x\mapsto (x,s(x))$
, so we may think of it as a function from X into
![]() $\tau (X)=X\times K^m$
with
$\tau (X)=X\times K^m$
with
![]() $\pi \circ s(x)=x$
.
$\pi \circ s(x)=x$
.
In addition, we still have for every generic
![]() $g\in X$
,
$g\in X$
,
![]() $g\in \Gamma \Leftrightarrow s(g)=\nabla _G(g)$
. By our assumptions, every generic
$g\in \Gamma \Leftrightarrow s(g)=\nabla _G(g)$
. By our assumptions, every generic
![]() ${\mathcal {L}}$
-type of X contains an element of
${\mathcal {L}}$
-type of X contains an element of
![]() $\Gamma $
; hence, the
$\Gamma $
; hence, the
![]() ${\mathcal {L}}$
-definable set
${\mathcal {L}}$
-definable set
![]() $X_0=\{x\in X:s(x)\in \tau (X)\}$
is large in X, so without loss of generality,
$X_0=\{x\in X:s(x)\in \tau (X)\}$
is large in X, so without loss of generality,
![]() $X=X_0$
. Let S be the graph of
$X=X_0$
. Let S be the graph of
![]() $s|X_0$
.
$s|X_0$
.
We claim that S satisfies the assumptions of Proposition 4.8: indeed, assume that
![]() $(a,b)$
is generic in
$(a,b)$
is generic in
![]() $S^2$
. Namely,
$S^2$
. Namely,
![]() $a=(g,s(g))$
and
$a=(g,s(g))$
and
![]() $b=(h,s(h))$
, for
$b=(h,s(h))$
, for
![]() $(g,h)$
generic in
$(g,h)$
generic in
![]() $X\times X$
. We need to prove that
$X\times X$
. We need to prove that
![]() $a b\in S$
.
$a b\in S$
.
By [Reference Peterzil, Pillay and Point15, Lemma 6.7], applied to the function
![]() $(s,s):X\times X\to \tau (X\times X)$
, there exists
$(s,s):X\times X\to \tau (X\times X)$
, there exists
![]() $(x,y)\in X\times X$
, realizing the same
$(x,y)\in X\times X$
, realizing the same
![]() ${\mathcal {L}}$
-type as
${\mathcal {L}}$
-type as
![]() $(g,h)$
such that
$(g,h)$
such that
![]() $\nabla _{G\times G}(x,y)=(s(x),s(y))$
. But then, by our assumptions,
$\nabla _{G\times G}(x,y)=(s(x),s(y))$
. But then, by our assumptions,
![]() $(x,y)\in \Gamma \times \Gamma $
, so
$(x,y)\in \Gamma \times \Gamma $
, so
![]() $xy\in \Gamma $
. Because
$xy\in \Gamma $
. Because
![]() $xy$
is still
$xy$
is still
![]() ${\mathcal {L}}$
-generic in G, we have
${\mathcal {L}}$
-generic in G, we have
![]() $xy\in X$
. Thus, we have
$xy\in X$
. Thus, we have
(where the middle equality follows from the fact that
![]() $\nabla _G$
is a group homomorphism). Since
$\nabla _G$
is a group homomorphism). Since
![]() $tp_{{\mathcal {L}}}(x,y)=tp_{{\mathcal {L}}}(g,h)$
, we also have
$tp_{{\mathcal {L}}}(x,y)=tp_{{\mathcal {L}}}(g,h)$
, we also have
![]() $s(gh)=s(g)s(h)$
, hence
$s(gh)=s(g)s(h)$
, hence
![]() $a b=(gh,s(gh))$
, is in S.
$a b=(gh,s(gh))$
, is in S.
We similarly prove that for a generic in S, we have
![]() $a^{-1}\in S$
; thus, S satisfies, indeed, the assumption of Proposition 4.8.
$a^{-1}\in S$
; thus, S satisfies, indeed, the assumption of Proposition 4.8.
Hence, there exists an
![]() ${\mathcal {L}}$
-definable
${\mathcal {L}}$
-definable
![]() $S_0\subseteq S$
, such that
$S_0\subseteq S$
, such that
![]() $S_0$
is a large subset of the group
$S_0$
is a large subset of the group
![]() $H=S_0\cdot S_0$
. Since
$H=S_0\cdot S_0$
. Since
![]() $S_0$
is large in H, for every generic
$S_0$
is large in H, for every generic
![]() $(g,s(g))\in H$
, we have
$(g,s(g))\in H$
, we have
![]() $\pi ^{-1}(g)\cap H$
is a singleton, which implies that
$\pi ^{-1}(g)\cap H$
is a singleton, which implies that
![]() $ker(\pi |H)=\{1\}$
, and hence H is the graph of a function. Also, since the group
$ker(\pi |H)=\{1\}$
, and hence H is the graph of a function. Also, since the group
![]() $\pi (H)$
is large in G, it necessarily equals to G.
$\pi (H)$
is large in G, it necessarily equals to G.
We therefore found an
![]() ${\mathcal {L}}$
-definable group-section
${\mathcal {L}}$
-definable group-section
![]() $\hat s:G\to \tau (G)$
, making
$\hat s:G\to \tau (G)$
, making
![]() $(G,\hat s)$
into a D-group. In addition,
$(G,\hat s)$
into a D-group. In addition,
![]() $x\in \Gamma \Leftrightarrow \hat s(x)=\nabla _G(x)$
, for all x generic in G.
$x\in \Gamma \Leftrightarrow \hat s(x)=\nabla _G(x)$
, for all x generic in G.
It is left to see that
Let
![]() $X_0=\pi (S_0)$
and
$X_0=\pi (S_0)$
and
![]() $\Gamma _0=X_0\cap \Gamma $
. By the definition of S,
$\Gamma _0=X_0\cap \Gamma $
. By the definition of S,
![]() $\Gamma =\{x\in \pi (S):S(x)=\nabla _G(x)\}$
, so
$\Gamma =\{x\in \pi (S):S(x)=\nabla _G(x)\}$
, so
![]() $\Gamma _0=\{x\in X_0:\hat s(x)=\nabla _G(x)\}.$
We claim that
$\Gamma _0=\{x\in X_0:\hat s(x)=\nabla _G(x)\}.$
We claim that
![]() $\Gamma _0\cdot \Gamma _0=\Gamma $
.
$\Gamma _0\cdot \Gamma _0=\Gamma $
.
Indeed, let
![]() $\gamma \in \Gamma $
, and pick g generic in
$\gamma \in \Gamma $
, and pick g generic in
![]() $X_0$
over
$X_0$
over
![]() $\gamma $
. By the geometric axioms, there exists
$\gamma $
. By the geometric axioms, there exists
![]() $\gamma _1\equiv _{{\mathcal {L}}(\gamma )} g$
such that
$\gamma _1\equiv _{{\mathcal {L}}(\gamma )} g$
such that
![]() $\hat s(\gamma _1)=\nabla _G(\gamma _1)$
, namely
$\hat s(\gamma _1)=\nabla _G(\gamma _1)$
, namely
![]() $\gamma _1\in \Gamma _0$
. It follows that
$\gamma _1\in \Gamma _0$
. It follows that
![]() $\gamma \cdot \gamma _1^{-1}$
is
$\gamma \cdot \gamma _1^{-1}$
is
![]() ${\mathcal {L}}$
-generic in G over
${\mathcal {L}}$
-generic in G over
![]() $\gamma $
and hence in
$\gamma $
and hence in
![]() $X_0$
, namely in
$X_0$
, namely in
![]() $\Gamma _0$
. Hence,
$\Gamma _0$
. Hence,
![]() $\gamma \in \Gamma _0\cdot \Gamma _0$
.
$\gamma \in \Gamma _0\cdot \Gamma _0$
.
It follows that for all
![]() $\gamma \in \Gamma $
, we have
$\gamma \in \Gamma $
, we have
![]() $\hat s(\gamma )=\nabla _G(\gamma )$
. To see the converse, assume that
$\hat s(\gamma )=\nabla _G(\gamma )$
. To see the converse, assume that
![]() $\hat s(x)=\nabla _G(x)$
, and choose
$\hat s(x)=\nabla _G(x)$
, and choose
![]() $\gamma \in \Gamma _0$
generic over x. We then have
$\gamma \in \Gamma _0$
generic over x. We then have
![]() $\hat s(\gamma )=\nabla _G(\gamma )$
, and
$\hat s(\gamma )=\nabla _G(\gamma )$
, and
![]() $x\cdot \gamma $
generic in
$x\cdot \gamma $
generic in
![]() $X_0$
. Because
$X_0$
. Because
![]() $\hat s$
is a homomorphism,
$\hat s$
is a homomorphism,
It follows that
![]() $x\gamma \in \Gamma $
and hence so is x. This ends the proof of Theorem 4.6.
$x\gamma \in \Gamma $
and hence so is x. This ends the proof of Theorem 4.6.
4.2 The case of p-adically closed fields
Let K be a p-adically closed field, namely a field which is elementarily equivalent to a finite extension of
![]() $\mathbb Q_p$
. The field admits a definable valuation, which we may add to the field language and call this language
$\mathbb Q_p$
. The field admits a definable valuation, which we may add to the field language and call this language
![]() ${\mathcal {L}}$
.
${\mathcal {L}}$
.
We shall use multiplicative notation for the valuation map
![]() $|\,|:K\to \{0\}\cup vK$
. Namely,
$|\,|:K\to \{0\}\cup vK$
. Namely,
and
For
![]() $a=(a_1,\ldots ,a_n)\in K^n$
, we write
$a=(a_1,\ldots ,a_n)\in K^n$
, we write
![]() $\| h\|=\max \{|a_i|:i=1,\ldots ,n\}.$
Since K is a geometric structure, we use the
$\| h\|=\max \{|a_i|:i=1,\ldots ,n\}.$
Since K is a geometric structure, we use the
![]() $acl$
-dimension below.
$acl$
-dimension below.
Definition 4.10 For
![]() $U\subseteq K^m$
open, a map
$U\subseteq K^m$
open, a map
![]() $f:U\to K^n$
is called differentiable at
$f:U\to K^n$
is called differentiable at
![]() $a\in U$
if there exists a K-linear map
$a\in U$
if there exists a K-linear map
![]() $T:K^m\to K^n$
such that for all
$T:K^m\to K^n$
such that for all
![]() $\epsilon \in vK$
there is
$\epsilon \in vK$
there is
![]() $\delta \in vK$
, such that for all
$\delta \in vK$
, such that for all
![]() $h\in K^m$
, if
$h\in K^m$
, if
![]() $\|h\|<\delta $
, then
$\|h\|<\delta $
, then
The linear map T can be identified with
![]() $Df_a$
the
$Df_a$
the
![]() $n\times m$
matrix of partial derivatives of f. We identify
$n\times m$
matrix of partial derivatives of f. We identify
![]() $M_{n\times m}(K)$
with
$M_{n\times m}(K)$
with
![]() $K^{n\cdot m}$
. The function f is called continuously differentiable on U, or
$K^{n\cdot m}$
. The function f is called continuously differentiable on U, or
![]() $C^1$
, if it is differentiable on U and the map
$C^1$
, if it is differentiable on U and the map
![]() $x\mapsto Df_a$
is continuous.
$x\mapsto Df_a$
is continuous.
Differentiable maps satisfy the chain rule, by the usual proof (see, for example, [Reference Schneider19, Remark 4.1] for a proof in
![]() $\mathbb Q_p$
).
$\mathbb Q_p$
).
Toward our main result, we first note that p-adically closed fields satisfy the assumptions in Remark 4.2: indeed, these are geometric fields with a definable Hausdorff, non-discrete topology. Let us see that they admit
![]() $C^1$
-cell decomposition (we could not find a precise reference for that in the literature).
$C^1$
-cell decomposition (we could not find a precise reference for that in the literature).
First, one can read-off analytic cell decomposition in finite extensions of
![]() $\mathbb Q_p$
from Scowcroft and van den Dries [Reference van den Dries and Scowcroft24, Sections 4 and 5]. More explicitly, the result is stated in [Reference Cluckers, Comte and Loeser5, Theorem 3.3] (as mentioned there, the theorem works for the Macintyre language, as well as the subanalytic one). Since being
$\mathbb Q_p$
from Scowcroft and van den Dries [Reference van den Dries and Scowcroft24, Sections 4 and 5]. More explicitly, the result is stated in [Reference Cluckers, Comte and Loeser5, Theorem 3.3] (as mentioned there, the theorem works for the Macintyre language, as well as the subanalytic one). Since being
![]() $C^1$
is a definable property, one may conclude a
$C^1$
is a definable property, one may conclude a
![]() $C^1$
-cell decomposition for definable sets in arbitrary elementarily equivalent structures, i.e., p-adically closed fields.
$C^1$
-cell decomposition for definable sets in arbitrary elementarily equivalent structures, i.e., p-adically closed fields.
Thus, as we commented in Remark 4.2, the result of Fact 4.1 holds in this setting as well and in particular, every
![]() ${\mathcal {L}}$
-definable group admits an
${\mathcal {L}}$
-definable group admits an
![]() ${\mathcal {L}}$
-definable
${\mathcal {L}}$
-definable
![]() $C^1$
-manifold which makes it into a
$C^1$
-manifold which makes it into a
![]() $C^1$
-group.
$C^1$
-group.
We now endow K with a derivation, denoted by
![]() $\partial $
. By Tressl’s work (see [Reference Tressl21, Theorem 7.2]), the theory of p-adically closed fields with a derivation has a model companion
$\partial $
. By Tressl’s work (see [Reference Tressl21, Theorem 7.2]), the theory of p-adically closed fields with a derivation has a model companion
![]() $T_{\partial }$
. In our one derivation case, (Tressl deals with several commuting derivations), one can axiomatize
$T_{\partial }$
. In our one derivation case, (Tressl deals with several commuting derivations), one can axiomatize
![]() $T_{\partial }$
with the following geometric axioms (see, for instance, [Reference Peterzil, Pillay and Point15, Fact 5.7(ii)]): whenever
$T_{\partial }$
with the following geometric axioms (see, for instance, [Reference Peterzil, Pillay and Point15, Fact 5.7(ii)]): whenever
![]() $(V,s)$
is an irreducible D-variety over K with a smooth K-point and U is a Zariski open subset of V defined over K, then there is
$(V,s)$
is an irreducible D-variety over K with a smooth K-point and U is a Zariski open subset of V defined over K, then there is
![]() $a\in U(K)$
such that
$a\in U(K)$
such that
![]() $(a,s(a))=\nabla (a)$
. (Recall that a D-variety
$(a,s(a))=\nabla (a)$
. (Recall that a D-variety
![]() $(V,s)$
defined over K is a K-variety V equipped with a rational section s defined over K from V to
$(V,s)$
defined over K is a K-variety V equipped with a rational section s defined over K from V to
![]() $T(V)$
[Reference Peterzil, Pillay and Point15, Definition 2.4].)
$T(V)$
[Reference Peterzil, Pillay and Point15, Definition 2.4].)
Now, exactly as in the work of Fornasiero and Kaplan for real closed fields [Reference Fornasiero and Kaplan6, Lemmas 2.4 and 2.7 and Proposition 2.8], every nontrivial derivation is compatible with the theory of p-adically closed fields, namely compatible with every
![]() ${\mathcal {L}}(\emptyset )$
-definable
${\mathcal {L}}(\emptyset )$
-definable
![]() $C^1$
map, as in Definition 3.1. We briefly review the details.
$C^1$
map, as in Definition 3.1. We briefly review the details.
As in [Reference Fornasiero and Kaplan6, Lemma 2.4], it is enough to verify compatibility of
![]() $\emptyset $
-definable
$\emptyset $
-definable
![]() $C^1$
-functions in neighborhoods of
$C^1$
-functions in neighborhoods of
![]() $acl_{\mathcal {L}}$
-independent points in
$acl_{\mathcal {L}}$
-independent points in
![]() $K^n$
(we use here the fact that
$K^n$
(we use here the fact that
![]() $acl_{\mathcal {L}}=dcl_{\mathcal {L}}$
). By quantifier elimination, the graph of every
$acl_{\mathcal {L}}=dcl_{\mathcal {L}}$
). By quantifier elimination, the graph of every
![]() ${\mathcal {L}}(\emptyset )$
-definable function
${\mathcal {L}}(\emptyset )$
-definable function
![]() $g{\kern-1.2pt}:{\kern-1.2pt}U{\kern-1.2pt}\to{\kern-1.2pt} K$
, for
$g{\kern-1.2pt}:{\kern-1.2pt}U{\kern-1.2pt}\to{\kern-1.2pt} K$
, for
![]() $U{\kern-1.2pt}\subseteq{\kern-1.2pt} K^n$
open, is given implicitly by
$U{\kern-1.2pt}\subseteq{\kern-1.2pt} K^n$
open, is given implicitly by
![]() $\{(x,{\kern-1pt}y){\kern-1.2pt}:{\kern-1.2pt}x{\kern-1.2pt}\in{\kern-1.2pt} U\& f(x,{\kern-1pt}y){\kern-1.2pt}={\kern-1.2pt}0\}$
, for
$\{(x,{\kern-1pt}y){\kern-1.2pt}:{\kern-1.2pt}x{\kern-1.2pt}\in{\kern-1.2pt} U\& f(x,{\kern-1pt}y){\kern-1.2pt}={\kern-1.2pt}0\}$
, for
![]() $f(x,y)$
an irreducible polynomial over
$f(x,y)$
an irreducible polynomial over
![]() $\mathbb Z$
. Now, if
$\mathbb Z$
. Now, if
![]() $a\in U$
is
$a\in U$
is
![]() ${\mathcal {L}}$
-generic over
${\mathcal {L}}$
-generic over
![]() $\emptyset $
, then
$\emptyset $
, then
![]() $(\partial f/\partial y)(a,g(a))\neq 0$
and as in [Reference Fornasiero and Kaplan6, Lemma 2.7],
$(\partial f/\partial y)(a,g(a))\neq 0$
and as in [Reference Fornasiero and Kaplan6, Lemma 2.7],
![]() $\partial $
is compatible with g.
$\partial $
is compatible with g.
In order to develop the rest of the theory as in the o-minimal case, we prove in the Appendix (see Proposition A.1) that definable functions in p-adically closed fields satisfy the analogue of Fact 3.4.
Proposition 4.11 Given an
![]() ${\mathcal {L}}(\emptyset )$
-definable
${\mathcal {L}}(\emptyset )$
-definable
![]() $W\subseteq K^n\times K^m$
and an
$W\subseteq K^n\times K^m$
and an
![]() ${\mathcal {L}}(\emptyset )$
-definable
${\mathcal {L}}(\emptyset )$
-definable
![]() $g:W\to K$
, if
$g:W\to K$
, if
![]() $(a,b)\in W$
,
$(a,b)\in W$
,
![]() $\dim (b/\emptyset )=m$
,
$\dim (b/\emptyset )=m$
,
![]() $W^b$
is open and
$W^b$
is open and
![]() $g(x,b)$
is a
$g(x,b)$
is a
![]() $C^1$
-function on
$C^1$
-function on
![]() $W^b$
, then
$W^b$
, then
![]() $(a,b)\in Int(W)$
and g is a
$(a,b)\in Int(W)$
and g is a
![]() $C^1$
-function at
$C^1$
-function at
![]() $(a,b)$
.
$(a,b)$
.
Now, the category of K-differentiable manifolds M and their associated functors T and
![]() $\tau $
can be developed identically to Sections 1 and 2. This allows us to associate to every definable group G the definable groups
$\tau $
can be developed identically to Sections 1 and 2. This allows us to associate to every definable group G the definable groups
![]() $T(G)$
and
$T(G)$
and
![]() $\tau (G)$
, such that the natural projections onto G are group homomorphisms. If G is a
$\tau (G)$
, such that the natural projections onto G are group homomorphisms. If G is a
![]() $C^1$
-group, then
$C^1$
-group, then
![]() $T(G)$
and
$T(G)$
and
![]() $\tau (G)$
are
$\tau (G)$
are
![]() $C^0$
-groups.
$C^0$
-groups.
By a p-adic D-group, we mean a pair
![]() $(G,s)$
where G is an
$(G,s)$
where G is an
![]() ${\mathcal {L}}$
-definable
${\mathcal {L}}$
-definable
![]() $C^1$
-group and
$C^1$
-group and
![]() $s:G\to \tau (G)$
an
$s:G\to \tau (G)$
an
![]() ${\mathcal {L}}$
-definable homomorphic section (i.e.,
${\mathcal {L}}$
-definable homomorphic section (i.e.,
![]() $\pi \circ s=id$
).
$\pi \circ s=id$
).
As before, we define in models of
![]() $T_{\partial }$
, given a D-group
$T_{\partial }$
, given a D-group
![]() $(G,s)$
,
$(G,s)$
,
In order to prove our main theorem in the p-adically closed field, we let T be the theory of p-adically closed fields and let
![]() $\Gamma $
be a finite-dimensional
$\Gamma $
be a finite-dimensional
![]() ${\mathcal {L}}_\partial $
-definable group in
${\mathcal {L}}_\partial $
-definable group in
![]() $K\models T_\partial $
. Since p-adically closed fields are large geometric fields, we may apply [Reference Peterzil, Pillay and Point15, Theorem 5.11] to conclude that Theorem 4.7 holds in this setting as well. Namely,
$K\models T_\partial $
. Since p-adically closed fields are large geometric fields, we may apply [Reference Peterzil, Pillay and Point15, Theorem 5.11] to conclude that Theorem 4.7 holds in this setting as well. Namely,
![]() $\Gamma $
embeds into an
$\Gamma $
embeds into an
![]() ${\mathcal {L}}$
-definable group G, with the additional
${\mathcal {L}}$
-definable group G, with the additional
![]() ${\mathcal {L}}$
-definable
${\mathcal {L}}$
-definable
![]() $X_i$
’s as in the theorem. Now we repeat word-for-word the proof in the o-minimal setting (see also Remark 4.2) to conclude the following theorem.
$X_i$
’s as in the theorem. Now we repeat word-for-word the proof in the o-minimal setting (see also Remark 4.2) to conclude the following theorem.
Theorem 4.12 Let T be the theory of p-adically closed fields, and let
![]() $\Gamma $
be a finite-dimensional
$\Gamma $
be a finite-dimensional
![]() $L_{\partial }$
-definable group in
$L_{\partial }$
-definable group in
![]() $K\models T_{\partial }$
. Then there exists an
$K\models T_{\partial }$
. Then there exists an
![]() ${\mathcal {L}}$
-definable D-group
${\mathcal {L}}$
-definable D-group
![]() $(G,s)$
such that
$(G,s)$
such that
![]() $\Gamma $
is definably isomorphic to
$\Gamma $
is definably isomorphic to
![]() $(G,s)^\partial $
.
$(G,s)^\partial $
.
4.3 The case of pseudo-finite fields
Let
![]() ${\mathcal {L}}$
be the language of rings, and let
${\mathcal {L}}$
be the language of rings, and let
![]() $C=(c_{i,n})_{n\in \mathbb N, i<n}$
be an infinite countable set of new constants. Let T be the
$C=(c_{i,n})_{n\in \mathbb N, i<n}$
be an infinite countable set of new constants. Let T be the
![]() ${\mathcal {L}}(C)$
-theory of pseudo-finite fields of characteristic
${\mathcal {L}}(C)$
-theory of pseudo-finite fields of characteristic
![]() $0$
, namely the theory of pseudo-algebraically closed fields plus the scheme of axioms saying, for every
$0$
, namely the theory of pseudo-algebraically closed fields plus the scheme of axioms saying, for every
![]() $n\in \mathbb N$
, that there is a unique extension of degree n, and that the polynomial
$n\in \mathbb N$
, that there is a unique extension of degree n, and that the polynomial
is irreducible.
Since T is a model-complete theory of large fields, one can apply the Tressl machinery and so the theory of differential expansions of models of T has a model-companion [Reference Tressl21, Corollary 8.4], which has been axiomatized [Reference Tressl21, Theorem 7.2] (in case of expansions by a single derivation, one obtains a geometric axiomatization [Reference Brouette, Cousins, Pillay and Point3, Lemma 1.6]). Recall that since T has almost q.e. (see [Reference Brouette, Cousins, Pillay and Point3, Remark 1.4(2)]), the theory
![]() $T_\partial $
does too [Reference Brouette, Cousins, Pillay and Point3, Definition 1.5 and Lemma 2.3], [Reference Tressl21, Theorem 7.2(iii)].
$T_\partial $
does too [Reference Brouette, Cousins, Pillay and Point3, Definition 1.5 and Lemma 2.3], [Reference Tressl21, Theorem 7.2(iii)].
Let
![]() ${\mathcal U}$
be our sufficiently saturated model of
${\mathcal U}$
be our sufficiently saturated model of
![]() $T_\partial $
, a differential expansion of a pseudo-finite field, and let
$T_\partial $
, a differential expansion of a pseudo-finite field, and let
![]() $\bar {\mathcal U}\supseteq \mathcal U$
be a saturated model of DCF
$\bar {\mathcal U}\supseteq \mathcal U$
be a saturated model of DCF
![]() $_0$
extending it. We work over a small submodel
$_0$
extending it. We work over a small submodel
![]() $(K,\partial )\models T_\partial $
.
$(K,\partial )\models T_\partial $
.
We briefly review the construction of the algebraic prolongation
![]() $\tau (V)\subseteq \bar {\mathcal U}^n\times \bar {\mathcal U}^n$
of an irreducible algebraic variety (see [Reference Marker14] for details).
$\tau (V)\subseteq \bar {\mathcal U}^n\times \bar {\mathcal U}^n$
of an irreducible algebraic variety (see [Reference Marker14] for details).
Assume that the ideal
![]() $I(V)$
is generated by polynomials
$I(V)$
is generated by polynomials
![]() $p_1,\ldots , p_m$
, over K, and let
$p_1,\ldots , p_m$
, over K, and let
![]() $P:\bar {\mathcal U}^n\to \bar {\mathcal U}^m$
be the corresponding polynomial map
$P:\bar {\mathcal U}^n\to \bar {\mathcal U}^m$
be the corresponding polynomial map
![]() $P(x)=(p_1(x),\ldots , p_m(x))$
. The definition of
$P(x)=(p_1(x),\ldots , p_m(x))$
. The definition of
![]() $DP$
and
$DP$
and
![]() $\tau (P)$
is defined as before using the formal derivative of polynomials (see also Remark 3.7). Then
$\tau (P)$
is defined as before using the formal derivative of polynomials (see also Remark 3.7). Then
and
Both are algebraic varieties over K. For
![]() $a\in V(\bar {\mathcal U})$
,
$a\in V(\bar {\mathcal U})$
,
![]() $a\mapsto \partial a$
is a section of
$a\mapsto \partial a$
is a section of
![]() ${\pi :\tau (V)\to V}$
, and we have
${\pi :\tau (V)\to V}$
, and we have
So,
![]() $\tau (V)_a$
is an affine translate of the vector space
$\tau (V)_a$
is an affine translate of the vector space
![]() $T(V)_a\subseteq \bar {\mathcal U}^n$
. In particular,
$T(V)_a\subseteq \bar {\mathcal U}^n$
. In particular,
![]() $\dim (\tau (V)_a)=\dim V$
.
$\dim (\tau (V)_a)=\dim V$
.
As described in [Reference Marker14], the above constructions of
![]() $T(V)$
and
$T(V)$
and
![]() $\tau (V)$
can be extended to abstract, not necessarily affine, algebraic varieties (which are covered by finitely many affine algebraic varieties). Furthermore, if H is an algebraic group, then
$\tau (V)$
can be extended to abstract, not necessarily affine, algebraic varieties (which are covered by finitely many affine algebraic varieties). Furthermore, if H is an algebraic group, then
![]() $T(H)$
and
$T(H)$
and
![]() $\tau (H)$
are algebraic groups with the property that the map
$\tau (H)$
are algebraic groups with the property that the map
![]() $\nabla _{H}$
is now a group morphism [Reference Marker14, Section 2].
$\nabla _{H}$
is now a group morphism [Reference Marker14, Section 2].
Our goal is to prove the following theorem.
Theorem 4.13 Let T be the theory of pseudo-finite fields, and let
![]() $\Gamma $
be a finite-dimensional definable group in
$\Gamma $
be a finite-dimensional definable group in
![]() $K\models T_{\partial }$
. Then there exists a K-algebraic D-group
$K\models T_{\partial }$
. Then there exists a K-algebraic D-group
![]() $(H, s)$
such that
$(H, s)$
such that
![]() $\Gamma $
is virtually definably isogenous over K to the K-points of
$\Gamma $
is virtually definably isogenous over K to the K-points of
![]() $(H,s)^\partial $
.
$(H,s)^\partial $
.
By “
![]() $\Gamma $
and
$\Gamma $
and
![]() $(H,s)^\partial (K)$
are virtually isogenous,” we mean the following: there exist an
$(H,s)^\partial (K)$
are virtually isogenous,” we mean the following: there exist an
![]() ${\mathcal {L}}_{\partial }$
-definable subgroup
${\mathcal {L}}_{\partial }$
-definable subgroup
![]() $\Gamma _0\subseteq \Gamma $
of finite index and an
$\Gamma _0\subseteq \Gamma $
of finite index and an
![]() ${\mathcal {L}}_{\partial }$
-definable homomorphism
${\mathcal {L}}_{\partial }$
-definable homomorphism
![]() $\sigma :\Gamma _0\to H$
with finite kernel, whose image has finite index in the K-points of
$\sigma :\Gamma _0\to H$
with finite kernel, whose image has finite index in the K-points of
![]() $(H,s)^\partial $
.
$(H,s)^\partial $
.
We first need the following lemma.
Lemma 4.14 Let
![]() $W_1, W_2$
be irreducible algebraic varieties over a differential field K, and
$W_1, W_2$
be irreducible algebraic varieties over a differential field K, and
![]() $a, b$
generic tuples in
$a, b$
generic tuples in
![]() $W_1$
and
$W_1$
and
![]() $W_2$
, respectively, over K. Suppose that a and b are field-theoretically interalgebraic over K (in particular,
$W_2$
, respectively, over K. Suppose that a and b are field-theoretically interalgebraic over K (in particular,
![]() $\dim W_1=\dim W_2$
), and let
$\dim W_1=\dim W_2$
), and let
![]() $W\subseteq W_1\times W_2$
be the (irreducible) variety over K with generic point
$W\subseteq W_1\times W_2$
be the (irreducible) variety over K with generic point
![]() $(a,b)$
. Then
$(a,b)$
. Then
![]() $\tau (W)_{(a,b)}$
is the graph of a bijection over
$\tau (W)_{(a,b)}$
is the graph of a bijection over
![]() $K(a,b)$
,
$K(a,b)$
,
![]() $\alpha :\tau (W_{1})_{a}\to \tau (W_{2})_{b}$
.
$\alpha :\tau (W_{1})_{a}\to \tau (W_{2})_{b}$
.
Proof This basically follows from the fact that the projection from W to
![]() $W_1,W_2$
is generically étale. However, for completeness, we include a proof. By dimension considerations, the affine space
$W_1,W_2$
is generically étale. However, for completeness, we include a proof. By dimension considerations, the affine space
![]() $\tau (W)_{(a,b)}$
projects onto both
$\tau (W)_{(a,b)}$
projects onto both
![]() $\tau (W_{1})_{a}$
and
$\tau (W_{1})_{a}$
and
![]() $\tau (W_{2})_{b}$
.
$\tau (W_{2})_{b}$
.
Fix some coordinate
![]() $a_{1}$
of the tuple a. By our interalgebraicity assumption,
$a_{1}$
of the tuple a. By our interalgebraicity assumption,
![]() $a_{1}$
is in the field-theoretic algebraic closure of
$a_{1}$
is in the field-theoretic algebraic closure of
![]() $K(b)$
. Let
$K(b)$
. Let
![]() $q(x)$
be the minimal monic polynomial of
$q(x)$
be the minimal monic polynomial of
![]() $a_{1}$
over
$a_{1}$
over
![]() $K(b)$
.
$K(b)$
.
![]() $q(x) = x^{n} + f_{n-1}(b)x^{n-1} + \cdots +f_{1}(b)x + f_{0}(b)$
, where the
$q(x) = x^{n} + f_{n-1}(b)x^{n-1} + \cdots +f_{1}(b)x + f_{0}(b)$
, where the
![]() $f_{i}(b)$
are K-rational functions of the tuple b. After getting rid of denominators, we can rewrite
$f_{i}(b)$
are K-rational functions of the tuple b. After getting rid of denominators, we can rewrite
![]() $q(x)$
as
$q(x)$
as
![]() $q_n(b)x^{n} + q_{n-1}(b)x^{n-1} + \cdots + q_{1}(b) x + q_{0}(b)$
where the
$q_n(b)x^{n} + q_{n-1}(b)x^{n-1} + \cdots + q_{1}(b) x + q_{0}(b)$
where the
![]() $q_{i}$
are polynomials over K.
$q_{i}$
are polynomials over K.
Hence,
![]() $r(x,y)$
:
$r(x,y)$
:
![]() $q_n(y)x^{n} + q_{n-1}(y)x^{n-1} + \cdots + q_{0}(y)$
is a polynomial (over K) in
$q_n(y)x^{n} + q_{n-1}(y)x^{n-1} + \cdots + q_{0}(y)$
is a polynomial (over K) in
![]() $I_{K}(W)$
.
$I_{K}(W)$
.
Hence,
![]() $(\partial r/\partial x)(a_{1}, b)(u_{1}) + \sum _{j}(\partial r/\partial y_{j})(a_{1},b)(v_{j}) + r^{\partial }(a_{1},b) = 0$
for
$(\partial r/\partial x)(a_{1}, b)(u_{1}) + \sum _{j}(\partial r/\partial y_{j})(a_{1},b)(v_{j}) + r^{\partial }(a_{1},b) = 0$
for
![]() $(u_{1},...,v_{1},...,v_{j},...)\in \tau (W)_{a,b}$
.
$(u_{1},...,v_{1},...,v_{j},...)\in \tau (W)_{a,b}$
.
By the minimality of
![]() $r(x,b)$
, we have
$r(x,b)$
, we have
![]() $\partial r/\partial x(a_1,b)\neq 0$
, and hence
$\partial r/\partial x(a_1,b)\neq 0$
, and hence
 $$ \begin{align*}u_{1} = \left(\sum_{j}(\partial r/\partial y_{j})(a_{1},b)(v_{j}) + r^{\partial}(a_{1},b))/ (\partial r/\partial x)(a_{1}, b)\right).\end{align*} $$
$$ \begin{align*}u_{1} = \left(\sum_{j}(\partial r/\partial y_{j})(a_{1},b)(v_{j}) + r^{\partial}(a_{1},b))/ (\partial r/\partial x)(a_{1}, b)\right).\end{align*} $$
Thus,
![]() $u_1\in dcl(K,a,b,v)$
. We similarly prove that u and v are inter-definable over
$u_1\in dcl(K,a,b,v)$
. We similarly prove that u and v are inter-definable over
![]() $K(a,b)$
. Since
$K(a,b)$
. Since
![]() $\tau (W)_{(a,b)}$
is a translate of a linear space, containing
$\tau (W)_{(a,b)}$
is a translate of a linear space, containing
![]() $(u,v)$
whose dimension equals
$(u,v)$
whose dimension equals
![]() $\dim W_1=\dim W_2$
, it must be the graph of a bijection.
$\dim W_1=\dim W_2$
, it must be the graph of a bijection.
We now return to the proof of Theorem 4.13.
By [Reference Peterzil, Pillay and Point15, Theorem 5.11], there exist an
![]() ${\mathcal {L}}$
-definable group G and a definable group embedding
${\mathcal {L}}$
-definable group G and a definable group embedding
![]() $:\sigma :\Gamma \to G$
. Furthermore, every generic
$:\sigma :\Gamma \to G$
. Furthermore, every generic
![]() ${\mathcal {L}}$
-type of G is realized by an element in
${\mathcal {L}}$
-type of G is realized by an element in
![]() $\sigma (\Gamma )$
and, in addition, there is a covering of G by finitely many
$\sigma (\Gamma )$
and, in addition, there is a covering of G by finitely many
![]() ${\mathcal {L}}(K)$
-definable sets
${\mathcal {L}}(K)$
-definable sets
![]() $X_i$
,
$X_i$
,
![]() $i=1,\ldots , m$
, and for each
$i=1,\ldots , m$
, and for each
![]() $X_i$
, there is a K-rational function
$X_i$
, there is a K-rational function
![]() $s_i:X_i\to \mathcal U^n$
such that for every
$s_i:X_i\to \mathcal U^n$
such that for every
![]() $a\in X_i(\mathcal U)$
which is
$a\in X_i(\mathcal U)$
which is
![]() ${\mathcal {L}}$
-generic in
${\mathcal {L}}$
-generic in
![]() $X_i$
over K, we have
$X_i$
over K, we have
For simplicity, we assume now that
![]() $\sigma =id$
, so
$\sigma =id$
, so
![]() $\Gamma \subseteq G$
.
$\Gamma \subseteq G$
.
We may take each
![]() $X_i$
to be Zariski dense in a K-variety
$X_i$
to be Zariski dense in a K-variety
![]() $V_i$
. We are only interested in those
$V_i$
. We are only interested in those
![]() $V_i$
whose Zariski dimension is maximal, call it d, so in particular, every algebraic type in
$V_i$
whose Zariski dimension is maximal, call it d, so in particular, every algebraic type in
![]() $V_i$
over K, of dimension d, is realized in
$V_i$
over K, of dimension d, is realized in
![]() $X_i$
in
$X_i$
in
![]() $\mathcal U$
, so by the axioms also realized by some
$\mathcal U$
, so by the axioms also realized by some
![]() $a\in X_i(\mathcal U)$
with
$a\in X_i(\mathcal U)$
with
![]() $\partial a=s_i(a)$
, and hence, by the above, also realized in
$\partial a=s_i(a)$
, and hence, by the above, also realized in
![]() $\Gamma $
. Finally, each
$\Gamma $
. Finally, each
![]() $X_i$
can be taken to be the
$X_i$
can be taken to be the
![]() $\mathcal U$
-points of
$\mathcal U$
-points of
![]() $W_i=Reg(V_i):=V_i\setminus Sing(V_i)$
, namely the
$W_i=Reg(V_i):=V_i\setminus Sing(V_i)$
, namely the
![]() $\mathcal U$
-points of a smooth quasi affine K-variety.
$\mathcal U$
-points of a smooth quasi affine K-variety.
We now apply [Reference Hrushovski and Pillay9, Theorem C] in the structure
![]() $\mathcal U$
: there exist a connected algebraic group H over K,
$\mathcal U$
: there exist a connected algebraic group H over K,
![]() ${\mathcal {L}}$
-definable subgroups of finite index,
${\mathcal {L}}$
-definable subgroups of finite index,
![]() $G_0\subseteq G$
and
$G_0\subseteq G$
and
![]() $H_0\subseteq H(\mathcal U)$
, and an
$H_0\subseteq H(\mathcal U)$
, and an
![]() ${\mathcal {L}}$
-definable surjective homomorphism
${\mathcal {L}}$
-definable surjective homomorphism
![]() $f:G_0\to H_0$
whose kernel is finite, all defined over K. The group H, as an algebraic group over K, has an associated K-algebraic group
$f:G_0\to H_0$
whose kernel is finite, all defined over K. The group H, as an algebraic group over K, has an associated K-algebraic group
![]() $\tau (H)$
. Notice that
$\tau (H)$
. Notice that
![]() $acl_{{\mathcal {L}}}$
equals the field
$acl_{{\mathcal {L}}}$
equals the field
![]() $acl$
and we have
$acl$
and we have
![]() $\dim H=d$
.
$\dim H=d$
.
Let
![]() $\Gamma _0=\Gamma \cap G_0$
, a subgroup of
$\Gamma _0=\Gamma \cap G_0$
, a subgroup of
![]() $\Gamma $
of finite index. Since
$\Gamma $
of finite index. Since
![]() $f(G_0)$
is Zariski dense in H, so is
$f(G_0)$
is Zariski dense in H, so is
![]() $f(\Gamma _0)$
. As we shall now see, we can endow H with the structure of a D-group,
$f(\Gamma _0)$
. As we shall now see, we can endow H with the structure of a D-group,
![]() $(H,s)$
such that
$(H,s)$
such that
Claim 4.15 For every
![]() $g\in \Gamma _0$
,
$g\in \Gamma _0$
,
![]() $tr.deg(\nabla _H f(g)/K)\leq \dim (H).$
$tr.deg(\nabla _H f(g)/K)\leq \dim (H).$
Proof We first prove the result for
![]() $g\in \Gamma _0$
such that
$g\in \Gamma _0$
such that
![]() $tr.deg(g/K)=d$
.
$tr.deg(g/K)=d$
.
Since
![]() $tr.deg(g/K)=d$
, there exists a K-algebraic quasi-affine variety
$tr.deg(g/K)=d$
, there exists a K-algebraic quasi-affine variety
![]() $W_i$
as above such that g is generic in
$W_i$
as above such that g is generic in
![]() $W_i$
over K. The
$W_i$
over K. The
![]() ${\mathcal {L}}$
-definable function f takes values in H, and because
${\mathcal {L}}$
-definable function f takes values in H, and because
![]() $acl_{{\mathcal {L}}}$
is the same as the field
$acl_{{\mathcal {L}}}$
is the same as the field
![]() $acl$
, there exists an algebraic correspondence
$acl$
, there exists an algebraic correspondence
![]() $C_i\subseteq W_i\times H$
over K, such that
$C_i\subseteq W_i\times H$
over K, such that
![]() $(g,f(g))$
is field-generic in
$(g,f(g))$
is field-generic in
![]() $C_i$
. It follows that
$C_i$
. It follows that
![]() $(\nabla _{W_i}(g),\nabla _H f(g))\in \tau (C_i)\subseteq \tau (W_i)\times \tau (H)$
.
$(\nabla _{W_i}(g),\nabla _H f(g))\in \tau (C_i)\subseteq \tau (W_i)\times \tau (H)$
.
By Lemma 4.14,
![]() $\tau (C_i)_{(g,f(g))}$
induces an (algebraic) bijection over K between
$\tau (C_i)_{(g,f(g))}$
induces an (algebraic) bijection over K between
![]() $\tau (W_i)_g$
and
$\tau (W_i)_g$
and
![]() $\tau (H)_{f(g)}$
. In particular,
$\tau (H)_{f(g)}$
. In particular,
![]() $\nabla _{W_i}(g)$
and
$\nabla _{W_i}(g)$
and
![]() $\nabla _H f(g)$
are interalgebraic over K. By our construction,
$\nabla _H f(g)$
are interalgebraic over K. By our construction,
![]() $\nabla _{W_i}(g)=s_i(g)$
; hence, g and
$\nabla _{W_i}(g)=s_i(g)$
; hence, g and
![]() $\nabla _H f(g)$
are interalgebraic over K (notice that g is algebraic over
$\nabla _H f(g)$
are interalgebraic over K (notice that g is algebraic over
![]() $\nabla _{W_i}(g)$
). Hence,
$\nabla _{W_i}(g)$
). Hence,
![]() $tr.deg(\nabla _H f(g)/K)= tr.deg(g/K)=d$
.
$tr.deg(\nabla _H f(g)/K)= tr.deg(g/K)=d$
.
Assume now that g is an arbitrary element of
![]() $\Gamma _0$
, and let
$\Gamma _0$
, and let
![]() $h\in \Gamma _0$
be such that
$h\in \Gamma _0$
be such that
![]() $tr.deg(h/K,g, \nabla _Hf(g))=d$
.
$tr.deg(h/K,g, \nabla _Hf(g))=d$
.
Since
![]() $tr.deg(hg/K)=d$
and
$tr.deg(hg/K)=d$
and
![]() $hg\in \Gamma _0$
, it follows from the above that
$hg\in \Gamma _0$
, it follows from the above that
and therefore
The elements
![]() $\nabla _Hf(h)\cdot \nabla _H f(g)$
and
$\nabla _Hf(h)\cdot \nabla _H f(g)$
and
![]() $\nabla _H f(g)$
are interalgebraic over K and
$\nabla _H f(g)$
are interalgebraic over K and
![]() $\nabla _Hf(h)$
, and thus
$\nabla _Hf(h)$
, and thus
![]() $tr.deg(\nabla _H f(g)/\nabla _H f(h),K)\leq d$
.
$tr.deg(\nabla _H f(g)/\nabla _H f(h),K)\leq d$
.
We know that h and
![]() $\nabla _{X_i}(h)$
(and hence also
$\nabla _{X_i}(h)$
(and hence also
![]() $\nabla _H f(h)$
) are interalgebraic over K (as witnessed by
$\nabla _H f(h)$
) are interalgebraic over K (as witnessed by
![]() $s_i$
), and as h and
$s_i$
), and as h and
![]() $\nabla _H(f(g))$
are independent over K, it follows that
$\nabla _H(f(g))$
are independent over K, it follows that
![]() $\nabla _H f(h)$
and
$\nabla _H f(h)$
and
![]() $\nabla _H f(g)$
are independent over K. Therefore,
$\nabla _H f(g)$
are independent over K. Therefore,
We now consider the subgroup
![]() $\nabla _H f(\Gamma _0)$
of
$\nabla _H f(\Gamma _0)$
of
![]() $\tau (H)$
and let
$\tau (H)$
and let
![]() $S\subseteq \tau (H)$
be its Zariski closure, an algebraic subgroup of
$S\subseteq \tau (H)$
be its Zariski closure, an algebraic subgroup of
![]() $\tau (H)$
. By the claim above,
$\tau (H)$
. By the claim above,
![]() $\dim (S)\leq \dim H$
, but since S contains
$\dim (S)\leq \dim H$
, but since S contains
![]() $\nabla _H f(h)$
for
$\nabla _H f(h)$
for
![]() ${\mathcal {L}}$
-generic
${\mathcal {L}}$
-generic
![]() $h\in \Gamma _0$
, we have
$h\in \Gamma _0$
, we have
![]() $\dim (S)=\dim (H)$
. Consider the projection
$\dim (S)=\dim (H)$
. Consider the projection
![]() $\pi :\tau (H)\to H$
, a group homomorphism, and its restriction to S. Since H is connected, we have
$\pi :\tau (H)\to H$
, a group homomorphism, and its restriction to S. Since H is connected, we have
![]() $\pi (S)=H$
, and hence
$\pi (S)=H$
, and hence
![]() $ker(\pi )\cap S$
is a finite subgroup of
$ker(\pi )\cap S$
is a finite subgroup of
![]() $\tau (H)_e$
. However,
$\tau (H)_e$
. However,
![]() $\tau (H)_e=T(H)_e$
is a vector space over K, a field of characteristic
$\tau (H)_e=T(H)_e$
is a vector space over K, a field of characteristic
![]() $0$
, thus torsion-free. Hence,
$0$
, thus torsion-free. Hence,
![]() $ker(\pi )\cap S$
is trivial, so
$ker(\pi )\cap S$
is trivial, so
![]() $\pi :S\to H$
is a group isomorphism. It follows that S can be viewed as a group section
$\pi :S\to H$
is a group isomorphism. It follows that S can be viewed as a group section
![]() $s:H\to \tau (H)$
. Since S is the Zariski closure of
$s:H\to \tau (H)$
. Since S is the Zariski closure of
![]() $\nabla _H(f(\Gamma _0))$
, we have for every
$\nabla _H(f(\Gamma _0))$
, we have for every
![]() $g\in \Gamma _0$
,
$g\in \Gamma _0$
,
![]() $\nabla _H(f(g))=s(f(g))$
.
$\nabla _H(f(g))=s(f(g))$
.
Recall that
![]() $H_0=f(G_0)$
is an
$H_0=f(G_0)$
is an
![]() ${\mathcal {L}}$
-definable subgroup of finite index of
${\mathcal {L}}$
-definable subgroup of finite index of
![]() $H(\mathcal U)$
.
$H(\mathcal U)$
.
Claim 4.16
![]() $f(\Gamma _0)=(H_0,s)^\partial =\{h\in H_0:\nabla _H(h)=s(h)\}.$
$f(\Gamma _0)=(H_0,s)^\partial =\{h\in H_0:\nabla _H(h)=s(h)\}.$
Proof We only need to prove the
![]() $\supseteq $
inclusion.
$\supseteq $
inclusion.
We first prove that for every
![]() $h\in (H_0,s)^\partial $
, if
$h\in (H_0,s)^\partial $
, if
![]() $tr.deg(h/K)=d$
, then
$tr.deg(h/K)=d$
, then
![]() $h\in f(\Gamma _0)$
. Indeed, since
$h\in f(\Gamma _0)$
. Indeed, since
![]() $h\in H_0$
is
$h\in H_0$
is
![]() ${\mathcal {L}}$
-generic in H over K, there exists
${\mathcal {L}}$
-generic in H over K, there exists
![]() $g\in G_0$
, necessarily
$g\in G_0$
, necessarily
![]() ${\mathcal {L}}$
-generic in G over K, such that
${\mathcal {L}}$
-generic in G over K, such that
![]() $h=f(g)$
. By our assumptions, there exists
$h=f(g)$
. By our assumptions, there exists
![]() $g'\in \Gamma $
, such that
$g'\in \Gamma $
, such that
![]() $g'$
and g realize the same
$g'$
and g realize the same
![]() ${\mathcal {L}}$
-type over K. Thus,
${\mathcal {L}}$
-type over K. Thus,
![]() $g'$
is in
$g'$
is in
![]() $G_0$
so also in
$G_0$
so also in
![]() $\Gamma _0$
. In addition,
$\Gamma _0$
. In addition,
![]() $f(g')$
and
$f(g')$
and
![]() $f(g)=h$
must realize the same
$f(g)=h$
must realize the same
![]() ${\mathcal {L}}$
-type over K. Because S is the Zariski closure of
${\mathcal {L}}$
-type over K. Because S is the Zariski closure of
![]() $\nabla _H f(\Gamma _0)$
, it follows that
$\nabla _H f(\Gamma _0)$
, it follows that
![]() $f(g')\in (H_0,s)^\partial $
.
$f(g')\in (H_0,s)^\partial $
.
Since
![]() $\nabla _H(h)=s(h)$
and
$\nabla _H(h)=s(h)$
and
![]() $\nabla _H(f(g'))=s(f(g'))$
, it follows that for every
$\nabla _H(f(g'))=s(f(g'))$
, it follows that for every
![]() $n\in \mathbb N$
, there is an
$n\in \mathbb N$
, there is an
![]() ${\mathcal {L}}(K)$
-definable function
${\mathcal {L}}(K)$
-definable function
![]() $s_n$
such that
$s_n$
such that
(recall that
![]() $\nabla _H^n(g)=(g,\partial g,\ldots ,\partial ^n g)$
). Because h and
$\nabla _H^n(g)=(g,\partial g,\ldots ,\partial ^n g)$
). Because h and
![]() $f(g')$
realize the same
$f(g')$
realize the same
![]() ${\mathcal {L}}$
-type over K, we may conclude that for every n,
${\mathcal {L}}$
-type over K, we may conclude that for every n,
![]() $\nabla _H^n(h)$
and
$\nabla _H^n(h)$
and
![]() $\nabla _H^n(f(g')))$
realize the same
$\nabla _H^n(f(g')))$
realize the same
![]() ${\mathcal {L}}$
-type over K, and therefore
${\mathcal {L}}$
-type over K, and therefore
(
![]() $\nabla _H^\infty (g)=(g,\partial g,\ldots , \partial ^n g,\ldots ).$
)
$\nabla _H^\infty (g)=(g,\partial g,\ldots , \partial ^n g,\ldots ).$
)
By [Reference Tressl21, 7.2(iii)], every
![]() ${\mathcal {L}}_{\partial }(K)$
-formula is equivalent in
${\mathcal {L}}_{\partial }(K)$
-formula is equivalent in
![]() $T_{\partial }$
to a Boolean combination of formulas of the form
$T_{\partial }$
to a Boolean combination of formulas of the form
![]() $(x,\partial x,\ldots ,\partial ^n x)\in Y$
, where Y is an
$(x,\partial x,\ldots ,\partial ^n x)\in Y$
, where Y is an
![]() ${\mathcal {L}}(K)$
definable set. Thus, it follows from the above that h and
${\mathcal {L}}(K)$
definable set. Thus, it follows from the above that h and
![]() $f(g')$
realize the same
$f(g')$
realize the same
![]() ${\mathcal {L}}_{\partial }$
-type over K, and therefore
${\mathcal {L}}_{\partial }$
-type over K, and therefore
![]() $h\in f(\Gamma _0)$
, as needed.
$h\in f(\Gamma _0)$
, as needed.
This proves that every
![]() $h\in (H_0,s)^\partial $
with
$h\in (H_0,s)^\partial $
with
![]() $tr.deg(h/K)=d$
belongs to
$tr.deg(h/K)=d$
belongs to
![]() $f(\Gamma _0)$
. However, every
$f(\Gamma _0)$
. However, every
![]() $h\in (H_0,s)^\partial $
can be written as
$h\in (H_0,s)^\partial $
can be written as
![]() $h=h_1h_2$
, with
$h=h_1h_2$
, with
![]() $h_1,h_2\in (H_0,s)^\partial $
and
$h_1,h_2\in (H_0,s)^\partial $
and
![]() $tr.deg(h_1/K)=tr.deg(h_2/K)=d$
. Indeed, pick
$tr.deg(h_1/K)=tr.deg(h_2/K)=d$
. Indeed, pick
![]() $h_1\in (H_0,s)^\partial $
with
$h_1\in (H_0,s)^\partial $
with
![]() $tr.deg(h_1/hK)=d$
and
$tr.deg(h_1/hK)=d$
and
![]() $h_2=h_1^{-1}h$
). Thus, every
$h_2=h_1^{-1}h$
). Thus, every
![]() $h\in (H_0,s)^\partial $
belongs to
$h\in (H_0,s)^\partial $
belongs to
![]() $f(\Gamma _0)$
. This ends the proof of Theorem 4.13.
$f(\Gamma _0)$
. This ends the proof of Theorem 4.13.
A Appendix
We fix K a p-adically closed field. All definability below is in the language
![]() ${\mathcal {L}}$
of K. Our goal is to prove the following p-adic analogue of Fornasiero–Kaplan’s theorem (see [Reference Fornasiero and Kaplan6, A.3]).
${\mathcal {L}}$
of K. Our goal is to prove the following p-adic analogue of Fornasiero–Kaplan’s theorem (see [Reference Fornasiero and Kaplan6, A.3]).
Proposition A.1 Let K be a p-adically closed field. Assume that
![]() $g:W\to K^r$
is an
$g:W\to K^r$
is an
![]() ${\mathcal {L}}(A)$
-definable partial function on some definable
${\mathcal {L}}(A)$
-definable partial function on some definable
![]() $W\subseteq K^n\times K^m$
, and
$W\subseteq K^n\times K^m$
, and
![]() $b\in \pi _2(W)\subseteq K^m$
is
$b\in \pi _2(W)\subseteq K^m$
is
![]() $acl_{{\mathcal {L}}}$
-independent over A.
$acl_{{\mathcal {L}}}$
-independent over A.
If
![]() $W^b=\{a\in K^n:(a,b)\in W\}$
is open and
$W^b=\{a\in K^n:(a,b)\in W\}$
is open and
![]() $g(x,b)$
is a
$g(x,b)$
is a
![]() $C^1$
-map on
$C^1$
-map on
![]() $W^b$
, then for every
$W^b$
, then for every
![]() $a\in W^b$
,
$a\in W^b$
,
![]() $(a,b)\in Int(W)$
and the function g is a
$(a,b)\in Int(W)$
and the function g is a
![]() $C^1$
-map (of all variables) in a neighborhood of
$C^1$
-map (of all variables) in a neighborhood of
![]() $(a,b)$
.
$(a,b)$
.
We shall use the following three important properties of p-adically closed fields (as well as o-minimal structures and some other geometric structures).
Fact A.2 Fix
![]() $A\subseteq K^{eq}$
.
$A\subseteq K^{eq}$
.
-
1. Given
 $a\in K^m$
and
$a\in K^m$
and
 $b\in K^n$
, if
$b\in K^n$
, if
 $U\ni a$
is a (definable) open set in
$U\ni a$
is a (definable) open set in
 $K^m$
, then there exists a definable open V,
$K^m$
, then there exists a definable open V,
 $a\in V\subseteq U$
, such that
$a\in V\subseteq U$
, such that
 $\dim (b/A[V])=\dim (b/A)$
(we use
$\dim (b/A[V])=\dim (b/A)$
(we use
 $[V]$
for the canonical parameter of V) (see [Reference Halevi, Hasson and Peterzil7, Corollary 3.13] or [Reference Johnson11, Lemma 4.30]).
$[V]$
for the canonical parameter of V) (see [Reference Halevi, Hasson and Peterzil7, Corollary 3.13] or [Reference Johnson11, Lemma 4.30]). -
2. Assume that
 $X\subseteq K^{m+n}$
is definable over A,
$X\subseteq K^{m+n}$
is definable over A,
 $a\in K^m, b\in K^n$
, and
$a\in K^m, b\in K^n$
, and
 $(a,b)\in X$
. Assume further that
$(a,b)\in X$
. Assume further that
 $X^b=\{x\in K^m:(x,b)\in X\}$
is finite. Then there exists a definable open
$X^b=\{x\in K^m:(x,b)\in X\}$
is finite. Then there exists a definable open
 $W\ni (a,b)$
(possibly over additional parameters) such that
$W\ni (a,b)$
(possibly over additional parameters) such that
 $X\cap W$
is the graph of a definable map from
$X\cap W$
is the graph of a definable map from
 $K^m$
to
$K^m$
to
 $K^n$
(this follows from cell decomposition in p-adically closed fields).
$K^n$
(this follows from cell decomposition in p-adically closed fields). -
3. If
 $U\subseteq K^m$
is open and
$U\subseteq K^m$
is open and
 $f:U\to K^n$
is an A-definable map, then f is
$f:U\to K^n$
is an A-definable map, then f is
 $C^1$
at every
$C^1$
at every
 $a\in U$
with
$a\in U$
with
 $\dim (a/A)=m$
(see [Reference van den Dries and Scowcroft24]).
$\dim (a/A)=m$
(see [Reference van den Dries and Scowcroft24]).
An immediate corollary of the first two is the following.
Fact A.3 For
![]() $a\in K^m$
and
$a\in K^m$
and
![]() $b\in K^n$
and
$b\in K^n$
and
![]() $A\subseteq K^{eq}$
, if
$A\subseteq K^{eq}$
, if
![]() $a\in acl(b,A)$
, then there exists
$a\in acl(b,A)$
, then there exists
![]() $A_1\supseteq A$
such that
$A_1\supseteq A$
such that
![]() $a\in dcl(bA_1)$
and
$a\in dcl(bA_1)$
and
![]() $\dim (b/A_1)=\dim (b/A)$
.
$\dim (b/A_1)=\dim (b/A)$
.
Proof of Proposition A.1
We first prove a continuous version.
Lemma A.4 Assume that
![]() $g:W\to K^r$
is an
$g:W\to K^r$
is an
![]() ${\mathcal {L}}(A)$
-definable partial function on some definable
${\mathcal {L}}(A)$
-definable partial function on some definable
![]() $W\subseteq K^m\times K^n$
, and
$W\subseteq K^m\times K^n$
, and
![]() $b\in \pi _2(W)\subseteq K^n$
is
$b\in \pi _2(W)\subseteq K^n$
is
![]() $acl_{{\mathcal {L}}}$
-independent over A. If
$acl_{{\mathcal {L}}}$
-independent over A. If
![]() ${W^b\subseteq K^m}$
is open and
${W^b\subseteq K^m}$
is open and
![]() $g(x,b)$
is continuous on
$g(x,b)$
is continuous on
![]() $W^b$
, then
$W^b$
, then
![]() $(a,b)\in Int(W)$
and for every
$(a,b)\in Int(W)$
and for every
![]() ${a\in X^b}$
, the function g is continuous at
${a\in X^b}$
, the function g is continuous at
![]() $(a,b)$
.
$(a,b)$
.
Proof We need the following claim.
Claim A.5 Assume that
![]() $X\subseteq K^m\times K^n$
is an A-definable set,
$X\subseteq K^m\times K^n$
is an A-definable set,
![]() $(a,b)\in X$
, and b is
$(a,b)\in X$
, and b is
![]() $acl_{\mathcal {L}}$
-independent in
$acl_{\mathcal {L}}$
-independent in
![]() $K^n$
over A. If
$K^n$
over A. If
![]() $a\in Int(X^b)$
, then
$a\in Int(X^b)$
, then
![]() $(a,b)\in Int(X)$
.
$(a,b)\in Int(X)$
.
Proof Applying Fact A.2(1), there is a definable open
![]() $V\ni a$
such that
$V\ni a$
such that
![]() $a\in V\subseteq X_b$
and
$a\in V\subseteq X_b$
and
![]() $\dim (b/A[V])=\dim (b/A)$
.
$\dim (b/A[V])=\dim (b/A)$
.
Because b is generic in
![]() $K^n$
over
$K^n$
over
![]() $A[V]$
, it remains generic in
$A[V]$
, it remains generic in
![]() $Y=\{b'\in K^n: V\subseteq X_{b'}\}$
. It follows that
$Y=\{b'\in K^n: V\subseteq X_{b'}\}$
. It follows that
![]() $\dim (Y)=n$
and
$\dim (Y)=n$
and
![]() $b\in Int(Y)$
, so
$b\in Int(Y)$
, so
![]() $(a,b)\in V\times Int(Y)\subseteq Int(X).$
$(a,b)\in V\times Int(Y)\subseteq Int(X).$
To prove the lemma, let
![]() $V\subseteq K^r$
be an open neighborhood of
$V\subseteq K^r$
be an open neighborhood of
![]() $g(a,b)$
. By Fact A.2(1), we may replace V by
$g(a,b)$
. By Fact A.2(1), we may replace V by
![]() $V_1$
,
$V_1$
,
![]() $g(a,b)\ni V_1\subseteq V$
, with b generic in
$g(a,b)\ni V_1\subseteq V$
, with b generic in
![]() $K^n$
over
$K^n$
over
![]() $A[V_1]$
. Consider the set
$A[V_1]$
. Consider the set
![]() $X=\{(x,y)\in W: f(x,y)\in V_1\}$
. We need to see that
$X=\{(x,y)\in W: f(x,y)\in V_1\}$
. We need to see that
![]() $(a,b)\in Int(X)$
. Since
$(a,b)\in Int(X)$
. Since
![]() $f(x,b)$
is continuous at a, we have
$f(x,b)$
is continuous at a, we have
![]() $a\in Int(X^b)$
, and hence by the above claim,
$a\in Int(X^b)$
, and hence by the above claim,
![]() $(a,b)\in Int(X)$
.
$(a,b)\in Int(X)$
.
We now return to the proof of Proposition A.1. Just like in [Reference Fornasiero and Kaplan6], we first reduce to the case where
![]() $a=0\in K^m$
and
$a=0\in K^m$
and
![]() $g(0,y)\equiv 0$
.
$g(0,y)\equiv 0$
.
After permuting a, we may write it as
![]() $a=(a_1,a_2)$
where
$a=(a_1,a_2)$
where
![]() $(a_2,b)$
is
$(a_2,b)$
is
![]() $acl$
-independent over A and
$acl$
-independent over A and
![]() $a_1\in acl(a_2bA)$
. Since
$a_1\in acl(a_2bA)$
. Since
![]() $W^b\subseteq K^m$
is open, the set
$W^b\subseteq K^m$
is open, the set
![]() $W^{(a_2,b)}$
, obtained by fixing additional parameters, is open in
$W^{(a_2,b)}$
, obtained by fixing additional parameters, is open in
![]() $K^{m-|a_2|}$
. Similarly,
$K^{m-|a_2|}$
. Similarly,
![]() $x_1\mapsto f(x_1,a_2,b)$
is still
$x_1\mapsto f(x_1,a_2,b)$
is still
![]() $C^1$
at
$C^1$
at
![]() $a_1$
(since
$a_1$
(since
![]() $f(x,b)$
was
$f(x,b)$
was
![]() $C^1$
at a). Thus, by replacing b with
$C^1$
at a). Thus, by replacing b with
![]() $(a_2,b)$
and a with
$(a_2,b)$
and a with
![]() $a_1$
, we may assume that
$a_1$
, we may assume that
![]() $a\in acl(bA)$
. By Fact A.3, we may add parameters to A while preserving the genericity of b, such that
$a\in acl(bA)$
. By Fact A.3, we may add parameters to A while preserving the genericity of b, such that
![]() $a\in dcl(bA)$
. We still use A for this new parameter set. Thus,
$a\in dcl(bA)$
. We still use A for this new parameter set. Thus,
![]() $b=\alpha (a)$
for an A-definable function
$b=\alpha (a)$
for an A-definable function
![]() $\alpha $
. Since b is generic in
$\alpha $
. Since b is generic in
![]() $dom(\alpha )$
, then
$dom(\alpha )$
, then
![]() $\alpha $
is continuously differentiable at b. Without loss of generality,
$\alpha $
is continuously differentiable at b. Without loss of generality,
![]() $dom(\alpha )=\pi _1(W)$
.
$dom(\alpha )=\pi _1(W)$
.
Consider the local
![]() $C^1$
-diffeomorphism
$C^1$
-diffeomorphism
![]() $\bar \alpha :(x,y)\mapsto (x-\alpha (y),y)$
. It sends W to a set
$\bar \alpha :(x,y)\mapsto (x-\alpha (y),y)$
. It sends W to a set
![]() $\bar W$
and
$\bar W$
and
![]() $(a,b)$
to
$(a,b)$
to
![]() $(0,b)$
, so by Fact A.5,
$(0,b)$
, so by Fact A.5,
![]() $(0,b)\in Int(\bar W)$
. The pushforward of g via
$(0,b)\in Int(\bar W)$
. The pushforward of g via
![]() $\bar \alpha $
is
$\bar \alpha $
is
![]() $\bar g(x,y)=g(x+\alpha (y),y)$
. The map
$\bar g(x,y)=g(x+\alpha (y),y)$
. The map
![]() $\bar g(x,b)$
is still
$\bar g(x,b)$
is still
![]() $C^1$
on
$C^1$
on
![]() $\bar W^b$
, and it is sufficient to prove that
$\bar W^b$
, and it is sufficient to prove that
![]() $\bar g$
is
$\bar g$
is
![]() $C^1$
at
$C^1$
at
![]() $(0,b)$
. So, we may replace g with
$(0,b)$
. So, we may replace g with
![]() $\bar g$
, W with
$\bar g$
, W with
![]() $\bar W$
, and
$\bar W$
, and
![]() $(a,b)$
with
$(a,b)$
with
![]() $(0,b)$
. We still use g and W for the sets. Finally, since b is generic in
$(0,b)$
. We still use g and W for the sets. Finally, since b is generic in
![]() $K^n$
, it follows from Fact A.2(3) that the function
$K^n$
, it follows from Fact A.2(3) that the function
![]() $g(0,y)$
is
$g(0,y)$
is
![]() $C^1$
in a neighborhood of b, so we may replace g with
$C^1$
in a neighborhood of b, so we may replace g with
![]() $g(x,y)-g(0,y)$
, and thus assume that
$g(x,y)-g(0,y)$
, and thus assume that
![]() $g(0,y)\equiv 0$
, and in particular,
$g(0,y)\equiv 0$
, and in particular,
![]() $D_yg_{(0,b)}=0$
, so
$D_yg_{(0,b)}=0$
, so
![]() $Dg_{(0,b)}=(D_xg_{(0,b)},0)\in M_{r\times (m+n)}(K)$
.
$Dg_{(0,b)}=(D_xg_{(0,b)},0)\in M_{r\times (m+n)}(K)$
.
To simplify notation below, we view
![]() $x\in K^n$
both as a row and a column vector, depending on context. Thus, for, say,
$x\in K^n$
both as a row and a column vector, depending on context. Thus, for, say,
![]() $(x,y)\in K^m\times K^n$
, we write
$(x,y)\in K^m\times K^n$
, we write
![]() $Dg_{{(a,b)}}\cdot (x,y)$
, instead of
$Dg_{{(a,b)}}\cdot (x,y)$
, instead of
![]() $Dg_{(a,b)}(x,y)^t$
.
$Dg_{(a,b)}(x,y)^t$
.
Notice that in order to show that g is differentiable at
![]() $(0,b)$
, we need to show that for every
$(0,b)$
, we need to show that for every
![]() $\epsilon \in vK$
, the point
$\epsilon \in vK$
, the point
![]() $(0,b)$
belongs to the interior of the set of
$(0,b)$
belongs to the interior of the set of
![]() $(x,y)\in K^m\times K^n$
, such that
$(x,y)\in K^m\times K^n$
, such that
which, since
![]() $g(0,b)=0$
and
$g(0,b)=0$
and
![]() $D_yg_{(0,b)}=0$
, equals
$D_yg_{(0,b)}=0$
, equals
We fix
![]() $\epsilon \in vK$
. By our assumption that
$\epsilon \in vK$
. By our assumption that
![]() $g(x,b)$
is differentiable at
$g(x,b)$
is differentiable at
![]() $0$
, it follows that
$0$
, it follows that
![]() $0$
is in the interior of
$0$
is in the interior of
By Claim A.5,
![]() $(0,b)$
is in the interior of
$(0,b)$
is in the interior of
hence, there exists
![]() $\delta _1\in vK$
such that if
$\delta _1\in vK$
such that if
![]() $\|(x,y-b)\|<\delta _1$
, then
$\|(x,y-b)\|<\delta _1$
, then
In order to prove that
![]() $(0,b)$
is in the interior of the set in (A.1), we write
$(0,b)$
is in the interior of the set in (A.1), we write
Claim A.6 There is
![]() $\delta _2\in vK$
, such that for all
$\delta _2\in vK$
, such that for all
![]() $(x,y)\in K^m\times K^n$
, if
$(x,y)\in K^m\times K^n$
, if
![]() $\|y-b\|<\delta _2$
, then
$\|y-b\|<\delta _2$
, then
Proof We first observe that for every
![]() $A=(a_{i,j})\in M_{n}(K)$
, if for all
$A=(a_{i,j})\in M_{n}(K)$
, if for all
![]() $i,j$
,
$i,j$
,
![]() $|a_{i,j}|<\epsilon $
, then for all
$|a_{i,j}|<\epsilon $
, then for all
![]() $x\in K^n$
, we have
$x\in K^n$
, we have
![]() $\|A\cdot x\|<\epsilon \|x\|.$
$\|A\cdot x\|<\epsilon \|x\|.$
Consider the map
![]() $G:K^n\to M_{r\times n}(K)$
, given by
$G:K^n\to M_{r\times n}(K)$
, given by
![]() $G(y)=D_xg_{(0,y)}$
(we identify the space on the right with
$G(y)=D_xg_{(0,y)}$
(we identify the space on the right with
![]() $K^{rn}$
). It is definable over A and hence continuous at b. Thus, there exists
$K^{rn}$
). It is definable over A and hence continuous at b. Thus, there exists
![]() $\delta _2\in vK$
such that whenever
$\delta _2\in vK$
such that whenever
![]() $\|y-b\|<\delta _2$
, then
$\|y-b\|<\delta _2$
, then
![]() $\|G(y)-G(b)\|=\|D_xg_{(0,y)}-D_xg_{(0,b)}\|<\epsilon .$
The result follows from our above observation.
$\|G(y)-G(b)\|=\|D_xg_{(0,y)}-D_xg_{(0,b)}\|<\epsilon .$
The result follows from our above observation.
If we now take
![]() $\delta =\min \{\delta _1,\delta _2\}$
, for
$\delta =\min \{\delta _1,\delta _2\}$
, for
![]() $\delta _2$
as in the above claim, then for all
$\delta _2$
as in the above claim, then for all
![]() $(x,y)\in K^m\times K^n$
with
$(x,y)\in K^m\times K^n$
with
![]() $\|(x,y-b)\|<\delta $
, we have, using (A.2),
$\|(x,y-b)\|<\delta $
, we have, using (A.2),
This ends the proof that
![]() $g(x,y)$
is differentiable at
$g(x,y)$
is differentiable at
![]() $(a,b)$
. Since
$(a,b)$
. Since
![]() $a\in W^b$
was arbitrary, it follows that for all
$a\in W^b$
was arbitrary, it follows that for all
![]() $x\in W^b$
,
$x\in W^b$
,
![]() $g(x,y)$
is differentiable at
$g(x,y)$
is differentiable at
![]() $(x,b)$
. Consider now the map
$(x,b)$
. Consider now the map
![]() $G:(x,y)\mapsto Dg_{(x,y)}$
. Since
$G:(x,y)\mapsto Dg_{(x,y)}$
. Since
![]() $g(x,b)$
is
$g(x,b)$
is
![]() $C^1$
on
$C^1$
on
![]() $W^b$
, the map
$W^b$
, the map
![]() $G(x,b)$
is continuous on
$G(x,b)$
is continuous on
![]() $W^b$
, and therefore by Lemma A.4, G is continuous at
$W^b$
, and therefore by Lemma A.4, G is continuous at
![]() $(a,b)$
. Thus, g is
$(a,b)$
. Thus, g is
![]() $C^1$
at
$C^1$
at
![]() $(a,b)$
. This ends the proof of Proposition A.1.
$(a,b)$
. This ends the proof of Proposition A.1.
Acknowledgements
We thank P. Scowcroft for his help and the anonymous referee for the thorough reading and useful suggestions.