Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-10T13:26:49.709Z Has data issue: false hasContentIssue false
  • English
  • Français

On Deformations of Pairs (Manifold, Coherent Sheaf)

Part of: Lie algebras and Lie superalgebras Commutative algebra: Homological methods Homological algebra Families, fibrations

Published online by Cambridge University Press:  09 January 2019

Donatella Iacono  and
Marco Manetti
Donatella Iacono
Affiliation:
Università degli Studi di Bari, Dipartimento di Matematica, Via E. Orabona 4, I-70125 Bari, Italy Email: donatella.iacono@uniba.it
Marco Manetti
Affiliation:
Università degli Studi di Roma “La Sapienza”, Dipartimento di Matematica “Guido Castelnuovo”, P.le Aldo Moro 5, I-00185 Roma, Italy Email: manetti@mat.uniroma1.it
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

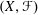We analyse infinitesimal deformations of pairs $(X,{\mathcal{F}})$ with 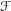${\mathcal{F}}$ a coherent sheaf on a smooth projective variety 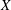$X$ over an algebraically closed field of characteristic 0. We describe a differential graded Lie algebra controlling the deformation problem, and we prove an analog of a Mukai–Artamkin theorem about the trace map.

Keywords

deformation of manifold and coherent sheafdifferential graded Lie algebra

MSC classification

Primary: 14D15: Formal methods; deformations
Secondary: 13D10: Deformations and infinitesimal methods 17B70: Graded Lie (super)algebras 18G50: Nonabelian homological algebra
Type
Article
Information
Canadian Journal of Mathematics , Volume 71 , Issue 5 , October 2019 , pp. 1209 - 1241
Copyright
© Canadian Mathematical Society 2018 

Footnotes

Author D. I. acknowledges the support of Fondi di Ateneo dell’Università di Bari. Author M. M. acknowledges the support by Italian MIUR under PRIN project 2015ZWST2C “Moduli spaces and Lie theory”.

References

Artamkin, I.V., On deformations of sheaves . Math. USSR Izvestiya 32(1989), no. 3, 663–668.Google Scholar
Atiyah, M., Complex analytic connections in fibre bundles . Trans. Am. Math. Soc. 85(1957), 181–207. https://doi.org/10.1090/S0002-9947-1957-0086359-5.Google Scholar
Bandiera, R. and Manetti, M., On coisotropic deformations of holomorphic submanifolds . J. Math. Sci. Univ. Tokyo 22(2015), no. 1, 1–37.Google Scholar
Eisenbud, D., Commutative algebra. With a view toward algebraic geometry . Graduate Texts in Mathematics, 150. Springer-Verlag, New York, 1995.Google Scholar
Fantechi, B., Göttsche, L., and van Straten, D., Euler number of the compactified Jacobian and multiplicity of rational curves . J. Algebraic Geometry 8(1999), 115–133.Google Scholar
Fiorenza, D., Iacono, D., and Martinengo, E., Differential graded Lie algebras controlling infinitesimal deformations of coherent sheaves . J. Eur. Math. Soc. (JEMS) 14(2012), no. 2, 521–540. arxiv:0904.1301. https://doi.org/10.4171/JEMS/310.Google Scholar
Fiorenza, D., Manetti, M., and Martinengo, E., Cosimplicial DGLAs in deformation theory . Communications in Algebra 40(2012), 2243–2260. https://doi.org/10.1080/00927872.2011.577479.Google Scholar
Goldman, W. M. and Millson, J. J., The deformation theory of representations of fundamental groups of compact Kähler manifolds . Inst. Hautes Études Sci. Publ. Math. (1988), no. 67, 43–96.Google Scholar
Grothendieck, A., Éléments de Géométrie Algébrique IV, quatrième partie . Publ. Math. IHES 32(1967), 5–361.Google Scholar
Hart, R., Derivations on commutative rings . J. London Math. Soc. (2) 8(1974), 171–175. https://doi.org/10.1112/jlms/s2-8.1.171.Google Scholar
Hartshorne, R., Algebraic geometry . Graduate Texts in Mathematics, 52. Springer-Verlag, New York, 1977.Google Scholar
Hovey, M., Model categories . Mathematical Surveys and Monographs, 63. American Mathematical Society, Providence, RI, 1999.Google Scholar
Huang, L., On joint moduli spaces . Math. Ann. 302(1995), 61–79. https://doi.org/10.1007/BF01444487.Google Scholar
Iacono, D., Deformations and obstructions of pairs (X, D) . Internat. Math. Res. Notices (IMRN) 2015 no. 19, 9660–9695. https://doi.org/10.1093/imrn/rnu242.Google Scholar
Iacono, D. and Manetti, M., Semiregularity and obstructions of complete intersections . Adv. Math. 235(2013), 92–125. https://doi.org/10.1016/j.aim.2012.11.011.Google Scholar
Kobayashi, S., Differential geometry of complex vector bundles . Publications of the Mathematical Society of Japan, 15. Princeton University Press, Princeton, NJ, 1987. https://doi.org/10.1515/9781400858682.Google Scholar
Manetti, M., Lectures on deformations of complex manifolds . Rend. Mat. Appl. (7) 24(2004), 1–183.Google Scholar
Manetti, M., Lie description of higher obstructions to deforming submanifolds . Ann. Sc. Norm. Super. Pisa Cl. Sci. 6(2007), 631–659. arxiv:math.AG/0507287.Google Scholar
Manetti, M., Differential graded Lie algebras and formal deformation theory. In: Algebraic Geometry–Seattle 2005. Proc. Sympos. Pure Math., 80. American Mathematical Society, Providence, NJ, 2009, pp. 785–810. https://doi.org/10.1090/pspum/080.2/2483955.Google Scholar
Manetti, M., On some examples of obstructed irregular surfaces . Sci. China Math. 54(2011), no. 8, 1713–1724. https://doi.org/10.1007/s11425-011-4248-z.Google Scholar
Matsumura, H., Commutative ring theory . Cambridge Studies in Advanced Mathematics, 8. Cambridge University Press, Cambridge, 1986.Google Scholar
Mukai, S., Symplectic structure of the moduli space of stable sheaves on an abelian or K3 surface . Invent. Math. 77(1984), 101–116. https://doi.org/10.1007/BF01389137.Google Scholar
Schlessinger, M., Functors of Artin rings . Trans. Amer. Math. Soc. 130(1968), 208–222. https://doi.org/10.1090/S0002-9947-1968-0217093-3.Google Scholar
Schürg, T., Toën, B., and Vezzosi, G., Derived algebraic geometry, determinants of perfect complexes, and applications to obstruction theories for maps and complexes . J. Reine Angew. Math. 702(2015), 1–40. https://doi.org/10.1515/crelle-2013-0037.Google Scholar
Sernesi, E., Deformations of algebraic schemes . Grundlehren der Mathematischen Wissenschaften, 334. Springer-Verlag, Berlin, 2006.Google Scholar
Teissier, B., The hunting invariants in the geometry of discriminants. In: Real and complex singularities. Sijthoff and Noordhoff, Alphen aan den Rijn, 1976, pp. 565–678.Google Scholar
Thomas, R., A holomorphic Casson invariant for Calabi-Yau 3-folds, and bundles on K3 fibrations . J. Differential Geom. 54(2000), no. 2, 367–438. https://doi.org/10.4310/jdg/1214341649.Google Scholar