Article contents
On directional Whitney inequality
Published online by Cambridge University Press: 26 February 2021
Abstract
This paper studies a new Whitney type inequality on a compact domain
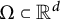 $\Omega \subset {\mathbb R}^d$
that takes the form
$\Omega \subset {\mathbb R}^d$
that takes the form
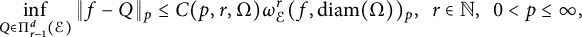
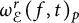 $\omega _{\mathcal {E}}^r(f, t)_p$
denotes the rth order directional modulus of smoothness of
$\omega _{\mathcal {E}}^r(f, t)_p$
denotes the rth order directional modulus of smoothness of
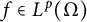 $f\in L^p(\Omega )$
along a finite set of directions
$f\in L^p(\Omega )$
along a finite set of directions
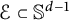 $\mathcal {E}\subset \mathbb {S}^{d-1}$
such that
$\mathcal {E}\subset \mathbb {S}^{d-1}$
such that
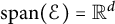 $\mathrm {span}(\mathcal {E})={\mathbb R}^d$
,
$\mathrm {span}(\mathcal {E})={\mathbb R}^d$
,
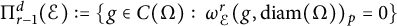 $\Pi _{r-1}^d(\mathcal {E}):=\{g\in C(\Omega ):\ \omega ^r_{\mathcal {E}} (g, \mathrm {diam} (\Omega ))_p=0\}$
. We prove that there does not exist a universal finite set of directions
$\Pi _{r-1}^d(\mathcal {E}):=\{g\in C(\Omega ):\ \omega ^r_{\mathcal {E}} (g, \mathrm {diam} (\Omega ))_p=0\}$
. We prove that there does not exist a universal finite set of directions
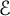 $\mathcal {E}$
for which this inequality holds on every convex body
$\mathcal {E}$
for which this inequality holds on every convex body
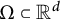 $\Omega \subset {\mathbb R}^d$
, but for every connected
$\Omega \subset {\mathbb R}^d$
, but for every connected
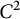 $C^2$
-domain
$C^2$
-domain
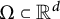 $\Omega \subset {\mathbb R}^d$
, one can choose
$\Omega \subset {\mathbb R}^d$
, one can choose
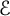 $\mathcal {E}$
to be an arbitrary set of d independent directions. We also study the smallest number
$\mathcal {E}$
to be an arbitrary set of d independent directions. We also study the smallest number
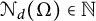 $\mathcal {N}_d(\Omega )\in {\mathbb N}$
for which there exists a set of
$\mathcal {N}_d(\Omega )\in {\mathbb N}$
for which there exists a set of
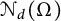 $\mathcal {N}_d(\Omega )$
directions
$\mathcal {N}_d(\Omega )$
directions
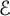 $\mathcal {E}$
such that
$\mathcal {E}$
such that
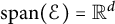 $\mathrm {span}(\mathcal {E})={\mathbb R}^d$
and the directional Whitney inequality holds on
$\mathrm {span}(\mathcal {E})={\mathbb R}^d$
and the directional Whitney inequality holds on
 $\Omega $
for all
$\Omega $
for all
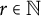 $r\in {\mathbb N}$
and
$r\in {\mathbb N}$
and
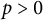 $p>0$
. It is proved that
$p>0$
. It is proved that
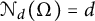 $\mathcal {N}_d(\Omega )=d$
for every connected
$\mathcal {N}_d(\Omega )=d$
for every connected
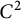 $C^2$
-domain
$C^2$
-domain
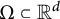 $\Omega \subset {\mathbb R}^d$
, for
$\Omega \subset {\mathbb R}^d$
, for
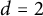 $d=2$
and every planar convex body
$d=2$
and every planar convex body
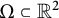 $\Omega \subset {\mathbb R}^2$
, and for
$\Omega \subset {\mathbb R}^2$
, and for
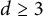 $d\ge 3$
and every almost smooth convex body
$d\ge 3$
and every almost smooth convex body
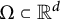 $\Omega \subset {\mathbb R}^d$
. For
$\Omega \subset {\mathbb R}^d$
. For
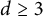 $d\ge 3$
and a more general convex body
$d\ge 3$
and a more general convex body
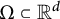 $\Omega \subset {\mathbb R}^d$
, we connect
$\Omega \subset {\mathbb R}^d$
, we connect
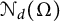 $\mathcal {N}_d(\Omega )$
with a problem in convex geometry on the X-ray number of
$\mathcal {N}_d(\Omega )$
with a problem in convex geometry on the X-ray number of
 $\Omega $
, proving that if
$\Omega $
, proving that if
 $\Omega $
is X-rayed by a finite set of directions
$\Omega $
is X-rayed by a finite set of directions
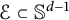 $\mathcal {E}\subset \mathbb {S}^{d-1}$
, then
$\mathcal {E}\subset \mathbb {S}^{d-1}$
, then
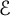 $\mathcal {E}$
admits the directional Whitney inequality on
$\mathcal {E}$
admits the directional Whitney inequality on
 $\Omega $
for all
$\Omega $
for all
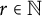 $r\in {\mathbb N}$
and
$r\in {\mathbb N}$
and
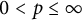 $0<p\leq \infty $
. Such a connection allows us to deduce certain quantitative estimate of
$0<p\leq \infty $
. Such a connection allows us to deduce certain quantitative estimate of
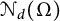 $\mathcal {N}_d(\Omega )$
for
$\mathcal {N}_d(\Omega )$
for
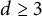 $d\ge 3$
.
$d\ge 3$
.
A slight modification of the proof of the usual Whitney inequality in literature also yields a directional Whitney inequality on each convex body
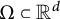 $\Omega \subset {\mathbb R}^d$
, but with the set
$\Omega \subset {\mathbb R}^d$
, but with the set
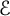 $\mathcal {E}$
containing more than
$\mathcal {E}$
containing more than
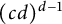 $(c d)^{d-1}$
directions. In this paper, we develop a new and simpler method to prove the directional Whitney inequality on more general, possibly nonconvex domains requiring significantly fewer directions in the directional moduli.
$(c d)^{d-1}$
directions. In this paper, we develop a new and simpler method to prove the directional Whitney inequality on more general, possibly nonconvex domains requiring significantly fewer directions in the directional moduli.
Keywords
MSC classification
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2021
Footnotes
The first author was supported by NSERC of Canada Discovery grant RGPIN-2020-03909, and the second author was supported by NSERC of Canada Discovery grant RGPIN-2020-05357.
References
- 2
- Cited by



