No CrossRef data available.
Article contents
On Functional Cesàro And Hölder Methods of Summability
Published online by Cambridge University Press: 20 November 2018
Extract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Suppose that f(x) is integrable L in every finite interval [0, X], and thatδ > 0. Define
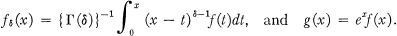
Information
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1976
References
1.
Borwein, D., On methods of summability based on integral functions, II,
Proc. Cambridge Philos. Soc.
56 (1960), 125–131.Google Scholar
3.
Riesz, M., Sur un théorème de la moyenne et ses applications,
Acta Sci. Math. (Szeged)
1 (1923), 114–126.Google Scholar
4.
Rogosinski, W. W., On Hausdorff's methods of summability, II,
Proc. Cambridge Philos. Soc.
38 (1942), 344–363.Google Scholar
5.
Shawyer, B. L. R., Iteration products of methods of summability and natural scales,
Manuscripta Math.
13 (1974), 355–364.Google Scholar
6.
Shawyer, B. L. R., On the product of the Cesar o and B or el-type methods of summability,
J. London Math. Soc. (2)
7 (1973), 111–116.Google Scholar

