Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-25T19:45:40.646Z Has data issue: false hasContentIssue false
  • English
  • Français

On Homotopy Invariants of Combings of Three-manifolds

Published online by Cambridge University Press:  20 November 2018

Christine Lescop
Christine Lescop*
Affiliation:
Institut Fourier, UJF Grenoble, CNRS, 100 rue des maths, BP 74, 38402 Saint-Martin d'Héres cedex, France email: Christine.Lescop@ujf-grenoble.fr
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Combings of compact, oriented, 3-dimensional manifolds 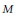$M$ are homotopy classes of nowhere vanishing vector fields. The Euler class of the normal bundle is an invariant of the combing, and it only depends on the underlying 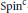$\text{Spi}{{\text{n}}^{\text{c}}}$-structure. A combing is called torsion if this Euler class is a torsion element of 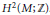${{H}^{2}}(M;\,\mathbb{Z})$. Gompf introduced a 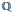$\mathbb{Q}$-valued invariant 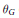${{\theta }_{G}}$ of torsion combings on closed 3-manifolds, and he showed that 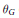${{\theta }_{G}}$ distinguishes all torsion combings with the same 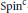$\text{Spi}{{\text{n}}^{\text{c}}}$-structure. We give an alternative definition for 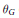${{\theta }_{G}}$ and we express its variation as a linking number. We define a similar invariant 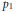${{p}_{1}}$ of combings for manifolds bounded by ${{S}^{2}}$. We relate 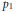${{p}_{1}}$ to the 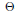$\Theta$-invariant, which is the simplest configuration space integral invariant of rational homology 3-balls, by the formula 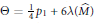$\Theta \,=\,\frac{1}{4}{{p}_{1}}\,+\,6\text{ }\!\!\lambda\!\!\text{ }\left( {\hat{M}} \right)$, where 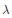$\text{ }\!\!\lambda\!\!\text{ }$ is the Casson-Walker invariant. The article also includes a self-contained presentation of combings for 3-manifolds.

Keywords

57M2757R2057N10Spinc-structurenowhere zero vector fieldsfirst Pontrjagin classEuler classHeegaard Floer homology gradingGompf invariantTheta invariantCasson-Walker invariantperturbative expansion of Chern-Simons theoryconfiguration space integrals
Type
Research Article
Information
Canadian Journal of Mathematics , Volume 67 , Issue 1 , 01 February 2015 , pp. 152 - 183
Copyright
Copyright © Canadian Mathematical Society 2015

References

[1] Akbulut, S. and McCarthy, J., Casson's invariant for oriented homology 3-spheres, Mathematical Notes, 36, Princeton University Press, Princeton, NJ, 1990.Google Scholar
[2] Cairns, S. S., Triangulation of the manifold of class one. Bull. Amer. Math. Soc., 41(1935), no. 8, 549–552.http://dx.doi.org/10.1090/S0002-9904-1935-06140-3 Google Scholar
[3] Dufraine, E., E., Classes d'homotopie de champs de vecteurs Morse-Smale sans singularité sur les fibrés de Seifert. Enseign. Math. (2) 51(2005), no. 1–2. 3–30.Google Scholar
[4] Gompf, R., Handlebody construction of Stein surfaces. Ann. of Math. (2), 148(1998), no. 2, 619–693.http://dx.doi.org/10.2307/121005 Google Scholar
[5] Gripp, V. and Huang, Y., An absolute grading on Heegaard Floer homology by homotopy classes of oriented 2-plane fields. arxiv:1112.0290v2 Google Scholar
[6] Guillou, L. and Marin, A., Notes sur l'invariant de Casson des sphéres d'homologie de dimension trois. Enseign. Math. (2) 38(1992), no. 3–4, 233–290.Google Scholar
[7] Hirsch, M., Differential topology. Graduate Texts in Mathematics, 33, Springer-Verlag, New York, 1994.Google Scholar
[8] Hirzebruch, F., Hilbert modular surfaces. Enseignement Math. (2) 19(1973), 183–281.Google Scholar
[9] Kaplan, S., Constructing framed 4-manifolds with given almost framed boundaries. Trans. Amer.Math. Soc. 254(1979), 237–263.http://dx.doi.org/10.2307/1998268 Google Scholar
[10] Kirby, R. and Melvin, P., Canonical framings for -manifolds. In: Proceedings of 6th Gökova Geometry-Topology Conference, Turkish J. Math. 23(1999), 89–115.Google Scholar
[11] Kirby, R., The topology of -manifolds. Lecture Notes in Mathematics, 1374, Springer-Verlag, Berlin, 1989.Google Scholar
[12] Kontsevich, M., Feynman diagrams and low-dimensional topology. In: First European Congress of Mathematics, Vol. II, (Paris, 1992), Progr. Math., 120, Birkhäuser, Basel, 1994, pp. 97–121.Google Scholar
[13] Kuperberg, G. and Thurston, D., Perturbative 3- invariants by cut-and-paste topology. 1999. arxiv:math.GT/9912167.Google Scholar
[14] Laudenbach, F., Formes différentielles de degré fermes non singulières: classes d'homotopie de leurs noyaux. Comment. Math. Helv. 51(1976), no. 3, 447–464.http://dx.doi.org/10.1007/BF02568169 Google Scholar
[15] Le, T. T. Q., Murakami, J., and T., Ohtsuki, T., On a universal perturbative invariant of -manifolds. Topology 37(1998), no. 3, 539–574.http://dx.doi.org/10.1016/S0040-9383(97)00035-9 Google Scholar
[16] Lescop, C., On the Kontsevich-Kuperberg-Thurston construction of a configuration-space invariant for rational homology 3-spheres. arxiv:math.GT/0411088 Google Scholar
[17] Lescop, C., Splitting formulae for the Kontsevich-Kuperberg-Thurston invariant of rational homology 3-spheres. arxiv:math.GT/0411431 Google Scholar
[18] Lescop, C., Invariants of knots and 3-manifolds derived from the equivariant linking pairing. In: Chern-Simons gauge theory: 20 years after, AMS/IP Stud. Adv. Math., 50, American Mathematical Society, Providence, RI, 2011, pp. 217–242.Google Scholar
[19] Lescop, C., A formula for the Θ-invariant from Heegaard diagrams. Geometry and Topology, to appear. arxiv:1209.3219v2 Google Scholar
[20] Lescop, C., An introduction to finite type invariants of knots and 3-manifolds defined by counting graph configurations. To appear, Quantum Topology Conference Proceedings (Vestnik ChelGU). arxiv:1312.2566 Google Scholar
[21] Marin, A., Un nouvel invariant pour les spèhres d'homologie de dimension trois (d'après Casson). Astérisque 161–162(1988), Exp. No. 693, 4, 151–164.Google Scholar
[22] Milnor, J.W., Topology from the differentiable viewpoint. Princeton Landmarks in Mathematics, Princeton University Press, Princeton, NJ, 1997.Google Scholar
[23] Milnor, J.W. and Stasheff, J. D., Characteristic classes. Annals of Mathematics Studies, 76, Princeton University Press, Princeton, NJ, 1974.Google Scholar
[24] Ozsváth, P. and Szabó, Z., Holomorphic disks and topological invariants for closed three-manifolds. Ann. of Math. (2) 159(2004), no. 3, 1027–1158.http://dx.doi.org/10.4007/annals.2004.159.102 Google Scholar
[25] Ozsváth, P. and Szabó, Z., Holomorphic triangles and invariants for smooth four-manifolds. Adv. Math. 202(2006), no. 2, 326–400,http://dx.doi.org/10.1016/j.aim.2005.03.014 Google Scholar
[26] Turaev, V., Torsion invariants of Spinc-structures on 3-manifolds. Math. Res. Lett. 4(1997), no. 5, 679–695.http://dx.doi.org/10.4310/MRL.1997.v4.n5.a6 Google Scholar
[27] Walker, K., An extension of Casson's invariant. Annals of Mathematics Studies, 126, Princeton University Press, Princeton, NJ, 1992.Google Scholar
[28] Witten, E., Quantum field theory and the Jones polynomial. Comm. Math. Phys. 121(1989), no. 3, 351–399. http://dx.doi.org/10.1007/BF01217730 Google Scholar